神经网络bp算法应用,bp神经网络动量因子

伤寒、副伤寒流行预测模型（BP神经网络）的建立

由于目前研究的各种数学模型或多或少存在使用条件的局限性，或使用方法的复杂性等问题，预测效果均不十分理想，距离实际应用仍有较大差距。

NNT是Matlab中较为重要的一个工具箱，在实际应用中，BP网络用的最广泛。

神经网络具有综合能力强，对数据的要求不高，适时学习等突出优点，其操作简便，节省时间，网络初学者即使不了解其算法的本质，也可以直接应用功能丰富的函数来实现自己的目的。

因此，易于被基层单位预防工作者掌握和应用。

以下几个问题是建立理想的因素与疾病之间的神经网络模型的关键：（1）资料选取应尽可能地选取所研究地区系统连续的因素与疾病资料，最好包括有疾病高发年和疾病低发年的数据。

在收集影响因素时，要抓住主要影响伤寒、副伤寒的发病因素。

（2）疾病发病率分级神经网络预测法是按发病率高低来进行预测，在定义发病率等级时，要结合专业知识及当地情况而定，并根据网络学习训练效果而适时调整，以使网络学习训练达到最佳效果。

（3）资料处理问题在实践中发现，资料的特征往往很大程度地影响网络学习和训练的稳定性，因此，数据的应用、纳入、排出问题有待于进一步研究。

6.3.1人工神经网络的基本原理人工神经网络（ANN）是近年来发展起来的十分热门的交叉学科，它涉及生物、电子、计算机、数学和物理等学科，有着广泛的应用领域。

人工神经网络是一种自适应的高度非线性动力系统，在网络计算的基础上，经过多次重复组合，能够完成多维空间的映射任务。

神经网络通过内部连接的自组织结构，具有对数据的高度自适应能力，由计算机直接从实例中学习获取知识，探求解决问题的方法，自动建立起复杂系统的控制规律及其认知模型。

人工神经网络就其结构而言，一般包括输入层、隐含层和输出层，不同的神经网络可以有不同的隐含层数，但他们都只有一层输入和一层输出。

神经网络的各层又由不同数目的神经元组成，各层神经元数目随解决问题的不同而有不同的神经元个数。

6.3.2BP神经网络模型BP网络是在1985年由PDP小组提出的反向传播算法的基础上发展起来的，是一种多层次反馈型网络（图6.17），它在输入和输出之间采用多层映射方式，网络按层排列，只有相邻层的节点直接相互连接，传递之间信息。

在正向传播中，输入信息从输入层经隐含层逐层处理，并传向输出层，每层神经元的状态只影响下一层神经元的状态。

如果输出层不能得到期望的输出结果，则转入反向传播，将误差信号沿原来的连同通路返回，通过修改各层神经元的权值，使误差信号最小。

BP网络的学习算法步骤如下（图6.18）：图6.17BP神经网络示意图图6.18BP算法流程图第一步：设置初始参数ω和θ，（ω为初始权重，θ为临界值，均随机设为较小的数）。

第二步：将已知的样本加到网络上，利用下式可算出他们的输出值yi，其值为岩溶地区地下水与环境的特殊性研究式中：xi为该节点的输入；ωij为从I到j的联接权；θj为临界值；yj为实际算出的输出数据。

第三步：将已知输出数据与上面算出的输出数据之差（dj-yj）调整权系数ω，调整量为ΔWij=ηδjxj式中：η为比例系数；xj为在隐节点为网络输入，在输出点则为下层（隐）节点的输出（j=1，2…，n）；dj为已知的输出数据（学习样本训练数据）；δj为一个与输出偏差相关的值，对于输出节点来说有δj=ηj（1-yj）（dj-yj）对于隐节点来说，由于它的输出无法进行比较，所以经过反向逐层计算有岩溶地区地下水与环境的特殊性研究其中k指要把上层（输出层）节点取遍。

误差δj是从输出层反向逐层计算的。各神经元的权值调整后为ωij（t）=ωij（t-1）+Vωij式中：t为学习次数。

这个算法是一个迭代过程，每一轮将各W值调整一遍，这样一直迭代下去，知道输出误差小于某一允许值为止，这样一个好的网络就训练成功了，BP算法从本质上讲是把一组样本的输入输出问题变为一个非线性优化问题，它使用了优化技术中最普遍的一种梯度下降算法，用迭代运算求解权值相当于学习记忆问题。

6.3.3BP神经网络模型在伤寒、副伤寒流行与传播预测中的应用伤寒、副伤寒的传播与流行同环境之间有着一定的联系。

根据桂林市1990年以来乡镇为单位的伤寒、副伤寒疫情资料，伤寒、副伤寒疫源地资料，结合现有资源与环境背景资料（桂林市行政区划、土壤、气候等）和社会经济资料（经济、人口、生活习惯等统计资料）建立人工神经网络数学模型，来逼近这种规律。

6.3.3.1模型建立（1）神经网络的BP算法BP网络是一种前馈型网络，由1个输入层、若干隐含层和1个输出层构成。

如果输入层、隐含层和输出层的单元个数分别为n，q1，q2，m，则该三层网络网络可表示为BP（n，q1，q2，m），利用该网络可实现n维输入向量Xn=（X1，X2，…，Xn）T到m维输出向量Ym=（Y1，Y2，…，Ym）T的非线性映射。

输入层和输出层的单元数n，m根据具体问题确定。

（2）样本的选取将模型的输入变量设计为平均温度、平均降雨量、岩石性质、岩溶发育、地下水类型、饮用水类型、正规自来水供应比例、集中供水比例8个输入因子（表6.29），输出单元为伤寒副伤寒的发病率等级，共一个输出单元。

其中q1，q2的值根据训练结果进行选择。表6.29桂林市伤寒副伤寒影响因素量化表通过分析，选取在伤寒副伤寒有代表性的县镇在1994～2001年的环境参评因子作为样本进行训练。

利用聚类分析法对疫情进行聚类分级（Ⅰ、Ⅱ、Ⅲ、Ⅳ），伤寒副伤寒发病最高级为Ⅳ（BP网络中输出定为4），次之的为Ⅲ（BP网络中输出定为3），以此类推，最低为Ⅰ（BP网络中输出定为1）（3）数据的归一化处理为使网络在训练过程中易于收敛，我们对输入数据进行了归一化处理，并将输入的原始数据都化为0～1之间的数。

如将平均降雨量的数据乘以0.0001；将平均气温的数据乘以0.01；其他输入数据也按类似的方法进行归一化处理。

（4）模型的算法过程假设共有P个训练样本，输入的第p个（p=1，2，…，P）训练样本信息首先向前传播到隐含单元上。

经过激活函数f（u）的作用得到隐含层1的输出信息：岩溶地区地下水与环境的特殊性研究经过激活函数f（u）的作用得到隐含层2的输出信息：岩溶地区地下水与环境的特殊性研究激活函数f（u）我们这里采用Sigmoid型，即f（u）=1/[1+exp（-u）]（6.5）隐含层的输出信息传到输出层，可得到最终输出结果为岩溶地区地下水与环境的特殊性研究以上过程为网络学习的信息正向传播过程。

另一个过程为误差反向传播过程。

如果网络输出与期望输出间存在误差，则将误差反向传播，利用下式来调节网络权重和阈值：岩溶地区地下水与环境的特殊性研究式中：Δω（t）为t次训练时权重和阈值的修正；η称为学习速率，0＜η＜1；E为误差平方和。

岩溶地区地下水与环境的特殊性研究反复运用以上两个过程，直至网络输出与期望输出间的误差满足一定的要求。该模型算法的缺点：1）需要较长的训练时间。

由于一些复杂的问题，BP算法可能要进行几小时甚至更长的时间的训练，这主要是由于学习速率太小造成的，可采用变化的学习速率或自适应的学习速率加以改进。2）完全不能训练。

主要表现在网络出现的麻痹现象上，在网络的训练过程中，当其权值调的过大，可能使得所有的或大部分神经元的加权总和n偏大，这使得激活函数的输入工作在S型转移函数的饱和区，从而导致其导数f′（n）非常小，从而使得对网络权值的调节过程几乎停顿下来。

3）局部极小值。BP算法可以使网络权值收敛到一个解，但它并不能保证所求为误差超平面的全局最小解，很可能是一个局部极小解。

这是因为BP算法采用的是梯度下降法，训练从某一起点沿误差函数的斜面逐渐达到误差的最小值。

考虑到以上算法的缺点，对模型进行了两方面的改进：（1）附加动量法为了避免陷入局部极小值，对模型进行了改进，应用了附加动量法。

附加动量法在使网络修正及其权值时，不仅考虑误差在梯度上的作用，而且考虑在误差曲面上变化趋势的影响，其作用如同一个低通滤波器，它允许网络忽略网络上的微小变化特性。

在没有附加动量的作用下，网络可能陷入浅的局部极小值，利用附加动量的作用则有可能滑过这些极小值。

该方法是在反向传播法的基础上在每一个权值的变化上加上一项正比于前次权值变化量的值，并根据反向传播法来产生心的权值变化。

促使权值的调节向着误差曲面底部的平均方向变化，从而防止了如Δω（t）=0的出现，有助于使网络从误差曲面的局部极小值中跳出。

这种方法主要是把式（6.7）改进为岩溶地区地下水与环境的特殊性研究式中：A为训练次数；a为动量因子，一般取0.95左右。

训练中对采用动量法的判断条件为岩溶地区地下水与环境的特殊性研究（2）自适应学习速率对于一个特定的问题，要选择适当的学习速率不是一件容易的事情。

通常是凭经验或实验获取，但即使这样，对训练开始初期功效较好的学习速率，不见得对后来的训练合适。

所以，为了尽量缩短网络所需的训练时间，采用了学习速率随着训练变化的方法来找到相对于每一时刻来说较差的学习速率。

下式给出了一种自适应学习速率的调整公式：岩溶地区地下水与环境的特殊性研究通过以上两个方面的改进，训练了一个比较理想的网络，将动量法和自适应学习速率结合起来，效果要比单独使用要好得多。

6.3.3.2模型的求解与预测采用包含了2个隐含层的神经网络BP（4，q1，q2，1），隐含层单元数q1，q2与所研究的具体问题有关，目前尚无统一的确定方法，通常根据网络训练情况采用试错法确定。

在满足一定的精度要求下一般认小的数值，以改善网络的概括推论能力。

在训练中网络的收敛采用输出值Ykp与实测值tp的误差平方和进行控制：岩溶地区地下水与环境的特殊性研究1）将附加动量法和自适应学习速率结合应用，分析桂林市36个乡镇地质条件各因素对伤寒副伤寒发病等级的影响。

因此训练样本为36个，第一个隐含层有19个神经元，第二个隐含层有11个神经元，学习速率为0.001。A.程序（略）。B.网络训练。

在命令窗口执行运行命令，网络开始学习和训练，其学习和训练过程如下（图6.19）。图6.19神经网络训练过程图C.模型预测。

a.输入未参与训练的乡镇（洞井乡、两水乡、延东乡、四塘乡、严关镇、灵田乡）地质条件数据。b.预测。程序运行后网络输出预测值a3，与已知的实际值进行比较，其预测结果整理后见（表6.30）。

经计算，对6个乡镇伤寒副伤寒发病等级的预测符合率为83.3%。表6.30神经网络模型预测结果与实际结果比较c.地质条件改进方案。

在影响疾病发生的地质条件中，大部分地质条件是不会变化的，而改变发病地区的饮用水类型是可以人为地通过改良措施加以实施的一个因素。

因此，以灵田乡为例对发病率较高的乡镇进行分析，改变其饮用水类型，来看发病等级的变化情况。

表6.31显示，在其他地质条件因素不变的情况下，改变当地的地下水类型（从原来的岩溶水类型改变成基岩裂隙水）则将发病等级从原来的最高级4级，下降为较低的2级，效果是十分明显的。

因此，今后在进行伤寒副伤寒疾病防治的时候，可以通过改变高发区饮用水类型来客观上减少疫情的发生。

表6.31灵田乡改变饮用水类型前后的预测结果2）选取桂林地区1994～2000年月平均降雨量、月平均温度作为输入数据矩阵，进行样本训练，设定不同的隐含层单元数，对各月份的数据进行BP网络训练。

在隐含层单元数q1=13，q2=9，经过46383次数的训练，误差达到精度要求，学习速率0.02。A.附加动量法程序（略）。B.网络训练。

在命令窗口执行运行命令，网络开始学习和训练，其学习和训练过程如下（图6.20）。C.模型预测。a.输入桂林市2001年1～12月桂林市各月份的平均气温和平均降雨量。预测程度（略）。b.预测。

程序运行后网络输出预测值a2，与已知的实际值进行比较，其预测结果整理后见（表6.32）。经计算，对2001年1～12月伤寒副伤寒发病等级进行预测，12个预测结果中，有9个符合，符合率为75%。

图6.20神经网络训练过程图表6.32神经网络模型预测结果与实际值比较6.3.3.3模型的评价本研究采用BP神经网络对伤寒、副伤寒发病率等级进行定量预测，一方面引用数量化理论对不确定因素进行量化处理；另一方面利用神经网络优点，充分考虑各影响因素与发病率之间的非线性映射。

实际应用表明，神经网络定量预测伤寒、副伤寒发病率是理想的。其主要优点有：1）避免了模糊或不确定因素的分析工作和具体数学模型的建立工作。2）完成了输入和输出之间复杂的非线性映射关系。

3）采用自适应的信息处理方式，有效减少人为的主观臆断性。虽然如此，但仍存在以下缺点：1）学习算法的收敛速度慢，通常需要上千次或更多，训练时间长。2）从数学上看，BP算法有可能存在局部极小问题。

本模型具有广泛的应用范围，可以应用在很多领域。从上面的结果可以看出，实际和网络学习数据总体较为接近，演化趋势也基本一致。

说明选定的气象因子、地质条件因素为神经单元获得的伤寒、副伤寒发病等级与实际等级比较接近，从而证明伤寒、副伤寒流行与地理因素的确存在较密切的相关性。

谷歌人工智能写作项目：小发猫

极端气温、降雨-洪水模型(BP神经网络)的建立

极端气温、降雨与洪水之间有一定的联系A8U神经网络。

根据1958～2007年广西西江流域极端气温、极端降雨和梧州水文站洪水数据，以第5章相关分析所确定的显著影响梧州水文站年最大流量的测站的相应极端气候因素(表4.22)为输入，建立人工神经网络模型。

4.5.1.1BP神经网络概述(1)基于BP算法的多层前馈网络模型采用BP算法的多层前馈网络是至今为止应用最广泛的神经网络，在多层的前馈网的应用中，如图4.20所示的三层前馈网的应用最为普遍，其包括了输入层、隐层和输出层。

图4.20典型的三层BP神经网络结构在正向传播中，输入信息从输入层经隐含层逐层处理，并传向输出层。

如果输出层不能得到期望的输出结果，则转入反向传播，将误差信号沿原来的连同通路返回，通过修改各层神经元的权值，使得误差最小。BP算法流程如图4.21所示。

图4.21BP算法流程图容易看出，BP学习算法中，各层权值调整均由3个因素决定，即学习率、本层输出的误差信号以及本层输入信号y(或x)。

其中，输出层误差信号同网络的期望输出与实际输出之差有关，直接反映了输出误差，而各隐层的误差信号与前面各层的误差信号都有关，是从输出层开始逐层反传过来的。

1988年，Cybenko指出两个隐含层就可表示输入图形的任意输出函数。

如果BP网络只有两个隐层，且输入层、第一隐含层、第二隐层和输出层的单元个数分别为n，p，q，m，则该网络可表示为BP(n，p，q，m)。

(2)研究区极端气温、极端降雨影响年最大流量过程概化极端气温、极端降雨影响年最大流量的过程极其复杂，从极端降雨到年最大流量，中间要经过蒸散发、分流、下渗等环节，受到地形、地貌、下垫面、土壤地质以及人类活动等多种因素的影响。

可将一个极端气候-年最大流量间复杂的水过程概化为小尺度的水系统，该水系统的主要影响因子可通过对年最大流量影响显著的站点的极端气温和极端降雨体现出来，而其中影响不明显的站点可忽略，从而使问题得以简化。

BP神经网络是一个非线形系统，可用于逼近非线形映射关系，也可用于逼近一个极为复杂的函数关系。极端气候-年最大流量水系统是一个非常复杂的映射关系，可将之概化为一个系统。

BP神经网络与研究流域的极端气候-年最大流量水系统的结构是相似的，利用BP神经网络，对之进行模拟逼近。

(3)隐含层单元数的确定隐含层单元数q与所研究的具体问题有关，目前尚无统一的确定方法，通常根据网络训练情况采用试错法确定。

在训练中网络的收敛采用输出值Ykp与实测值tp的误差平方和进行控制变环境条件下的水资源保护与可持续利用研究作者认为，虽然现今的BP神经网络还是一个黑箱模型，其参数没有水文物理意义，在本节的研究过程中，将尝试着利用极端气候空间分析的结果来指导隐含层神经元个数的选取。

(4)传递函数的选择BP神经网络模型算法存在需要较长的训练时间、完全不能训练、易陷入局部极小值等缺点，可通过对模型附加动量项或设置自适应学习速率来改良。

本节采用MATLAB工具箱中带有自适应学习速率进行反向传播训练的traingdm(　)函数来实现。

(5)模型数据的归一化处理由于BP网络的输入层物理量及数值相差甚远，为了加快网络收敛的速度，使网络在训练过程中易于收敛，对输入数据进行归一化处理，即将输入的原始数据都化为0～1之间的数。

本节将年极端最高气温的数据乘以0.01;将极端最低气温的数据乘以0.1;年最大1d、3d、7d降雨量的数据乘以0.001;梧州水文站年最大流量的数据乘以0.00001，其他输入数据也按类似的方法进行归一化处理。

(6)年最大流量的修正梧州水文站以上的流域集水面积为32.70万km2，广西境内流域集水面积为20.24万km2，广西境内流域集水面积占梧州水文站以上的流域集水面积的61.91%。

因此，选取2003～2007年梧州水文站年最大流量和红水河的天峨水文站年最大流量，分别按式4.10计算每年的贡献率(表4.25)，取其平均值作为广西西江流域极端降雨对梧州水文站年最大流量的平均贡献率，最后确定平均贡献率为76.88%。

变环境条件下的水资源保护与可持续利用研究表4.252003～2007年极端降雨对梧州水文站年最大流量的贡献率建立“年极端气温、降雨与梧州年最大流量模型”时，应把平均贡献率与梧州水文站年最大流量的乘积作为模型输入的修正年最大流量，而预测的年最大流量应该为输出的年最大流量除以平均贡献率76.88%，以克服极端气温和降雨研究范围与梧州水文站集水面积不一致的问题。

4.5.1.2年极端气温、年最大1d降雨与梧州年最大流量的BP神经网络模型(1)模型的建立以1958～1997年年极端最高气温、年极端最低气温、年最大1d降雨量与梧州水文站年最大流量作为学习样本拟合、建立“年极端气温、年最大1d降雨-梧州年最大流量BP神经网络模型”。

以梧州气象站的年极端最高气温，桂林、钦州气象站的年极端最低气温，榜圩、马陇、三门、黄冕、沙街、勾滩、天河、百寿、河池、贵港、金田、平南、大化、桂林、修仁、五将雨量站的年最大1d降雨量为输入，梧州水文站年最大流量为输出，隐含层层数取2，建立(19，p，q，1)BP神经网络模型，其中神经元数目p，q经试算分别取16和3，第一隐层、第二隐层的神经元采用tansig传递函数，输出层的神经元采用线性传递函数，训练函数选用traingdm，学习率取0.1，动量项取0.9，目标取0.0001，最大训练次数取200000。

BP网络模型参数见表4.26，结构如图4.22所示。

图4.22年极端气温、年最大1d降雨-梧州年最大流量BP模型结构图表4.26BP网络模型参数一览表从结构上分析，梧州水文站年最大流量产生过程中，年最高气温、年最低气温和各支流相应的流量都有其阈值，而极端气温和极端降雨是其输入，年最大流量是其输出，这类似于人工神经元模型中的阈值、激活值、输出等器件。

输入年最大1d降雨时选用的雨量站分布在14条支流上(表4.27)，极端降雨发生后，流经14条支流汇入梧州，在这一过程中极端气温的变化影响极端降雨的蒸散发，选用的雨量站分布在年最大1d降雨四个自然分区的Ⅱ、Ⅲ、Ⅳ3个区。

该过程可与BP神经网络结构进行类比(表4.28)，其中，14条支流相当于第一隐含层中的14个神经元，年最高气温和年最低气温相当于第一隐含层中的2个神经元，年最大1d降雨所在的3个分区相当于第二隐含层的3个神经元，年最高气温、年最低气温的影响值和各支流流量的奉献值相当于隐含层中人工神经元的阈值，从整体上来说，BP神经网络的结构已经灰箱化。

表4.27选用雨量站所在支流一览表表4.28BP神经网络构件物理意义一览表(2)训练效果分析训练样本为40个，经过113617次训练，达到精度要求。

在命令窗口执行运行命令，网络开始学习和训练，其训练过程如图4.23所示，训练结果见表4.29和图4.24。

表4.29年最大流量训练结果图4.23神经网络训练过程图图4.24年最大流量神经网络模型训练结果从图4.26可知，训练后的BP网络能较好地逼近给定的目标函数。

从训练样本检验结果(表4.5)可得:1958～1997年40年中年最大流量模拟值与实测值的相对误差小于10%和20%的分别为39年，40年，合格率为100%。

说明“年极端气温、年最大1d降雨-梧州年最大流量预测模型”的实际输出与实测结果误差很小，该模型的泛化能力较好，模拟结果较可靠。

(3)模型预测检验把1998～2007年梧州气象站的年极端最高气温，桂林、钦州气象站的年极端最低气温，榜圩、马陇、三门、黄冕、沙街、勾滩、天河、百寿、河池、贵港、金田、平南、大化、桂林、修仁、五将雨量站的年最大1d降雨量输入到“年极端气温、年最大1d降雨梧州年最大流量BP神经网络模型”。

程序运行后网络输出预测值与已知的实际值进行比较，其预测检验结果见图4.25，表4.30。

图4.25年最大流量神经网络模型预测检验结果表4.30神经网络模型预测结果与实际结果比较从预测检验结果可知:1998～2007年10年中年最大流量模拟值与实测值的相对误差小于20%的为9年，合格率为90%，效果较好。

4.5.1.3年极端气温、年最大7d降雨与梧州年最大流量的BP神经网络模型(1)模型的建立以1958～1997年年极端最高气温、年极端最低气温、年最大7d降雨量和梧州水文站年最大流量作为学习样本来拟合、建立“年极端气温、年最大7d降雨-梧州年最大流量BP神经网络模型”。

以梧州气象站的年极端最高气温，桂林、钦州气象站的年极端最低气温，凤山、都安、马陇、沙街、大湟江口、大安、大化、阳朔、五将雨量站的年最大7d降雨量为输入，梧州水文站年最大流量为输出，隐含层层数取2，建立(12，p，q，1)BP神经网络模型，其中，神经元数目p，q经试算分别取10和4，第一隐层、第二隐层的神经元采用tansig传递函数，输出层的神经元采用线性传递函数，训练函数选用traingdm，学习率取0.1，动量项取0.9，目标取0.0001，最大训练次数取200000。

BP网络模型参数见表4.31，结构如图4.26所示。

表4.31BP网络模型参数一览表图4.26年极端气温、年最大7d降雨-梧州年最大流量BP模型结构图本节输入年最大7d降雨时选用的雨量站分布在8条支流上(表4.32)，在发生极端降雨后，流经8条支流汇入梧州，在这一过程中极端气温的变化影响极端降雨的蒸散发，且选用的雨量站分布在年最大7d降雨四个自然分区的Ⅰ、Ⅱ、Ⅲ、Ⅳ4个区中。

该过程可与BP神经网络结构进行类比(表4.33)，其中，8条支流相当于第一隐含层中的8个神经元，年最高气温和年最低气温相当于第一隐含层中的2个神经元，年最大7d降雨所在的4个分区相当于第二隐含层的4个神经元，整体上来说，BP神经网络的结构已经灰箱化。

表4.32选用雨量站所在支流一览表表4.33BP神经网络构件物理意义一览表(2)训练效果分析训练样本为40个，经过160876次的训练，达到精度要求，在命令窗口执行运行命令，网络开始学习和训练，其训练过程如图4.27所示，训练结果见表4.34，图4.28。

图4.27神经网络训练过程图表4.34年最大流量训练结果图4.28年最大流量神经网络模型训练结果从图4.28可知，训练后的BP网络能较好地逼近给定的目标函数。

由训练样本检验结果(表4.34)可得:1958～1997年40年中年最大流量模拟值与实测值的相对误差小于10%和20%的，分别为38年、40年，合格率为100%。

说明“年极端气温、年最大7d降雨-梧州年最大流量BP神经网络模型”的泛化能力较好，模拟的结果较可靠。

(3)模型预测检验把1998～2007年梧州气象站的年极端最高气温，桂林、钦州气象站的年极端最低气温，凤山、都安、马陇、沙街、大湟江口、大安、大化、阳朔、五将雨量站的年最大7d降雨量输入到“年极端气温、年最大7d降雨-梧州年最大流量BP神经网络模型”。

程序运行后网络输出预测值与已知的实际值进行比较，其预测结果见图4.29和表4.35。

图4.29年最大流量神经网络模型预测检验结果表4.35神经网络模型预测结果与实际结果比较由预测检验结果可知:1998～2007年10年中年最大流量模拟值与实测值的相对误差小于20%的为7年，合格率为70%，效果较好。

4.5.1.4梧州年最大流量-年最高水位的BP神经网络模型(1)模型的建立以1941～1997年梧州水文站的年最大流量与年最高水位作为学习样本来拟合、建立梧州水文站的“年最大流量-年最高水位BP神经网络模型”。

以年最大流量为输入，年最高水位为输出，隐含层层数取1，建立(1，q，1)BP神经网络模型，其中，神经元数目q经试算取7，隐含层、输出层的神经元采用线性传递函数，训练函数选用traingdm，学习率取0.1，动量项取0.9，目标取0.00001，最大训练次数取200000。

BP网络模型参数见表4.36，结构如图4.30所示。

表4.36BP网络模型参数一览表图4.30梧州年最大流量—年最高水位BP模型结构图广西西江流域主要河流有南盘江、红水河、黔浔江、郁江、柳江、桂江、贺江。

7条主要河流相当于隐含层中的7个神经元(表4.37)，整体上来说，BP神经网络的结构已经灰箱化。

表4.37BP神经网络构件物理意义一览表(2)训练效果分析训练样本为57个，经过3327次训练，误差下降梯度已达到最小值，但误差为3.00605×10-5，未达到精度要求。

在命令窗口执行运行命令，网络开始学习和训练，其训练过程如图4.31所示，训练结果见图4.32和表4.38。

表4.38年最高水位训练结果从图4.32和表4.19可看出，训练后的BP网络能较好地逼近给定的目标函数。

对于训练样本，从检验结果可知:1941～1997年57年中年最高水位模拟值与实测值的相对误差小于10%和20%的分别为56a，57a，合格率为100%。

说明“年最大流量-年最高水位BP神经网络模型”的实际输出与实测结果误差很小，该模型的泛化能力较好，模拟的结果比较可靠。

图4.31神经网络训练过程图图4.32年最高水位神经网络模型训练结果(3)模型预测检验把1998～2007年梧州水文站年最大流量输入到“年最大流量-年最高水位BP神经网络模型”。

程序运行后网络输出预测值与已知的实际值进行比较，其预测结果见图4.33，表4.39。

表4.39神经网络模型预测结果与实际结果比较从预测检验结果可知:1998～2007年10年中，年最高水位模拟值与实测值的相对误差小于20%的为10年，合格率为100%，效果较好。

图4.33年最高水位量神经网络模型预测检验结果。

bp神经网络收敛问题

当然是越慢。因为已经接近最低点，训练也进入误差曲面的平坦区，每次搜索的误差下降速度是减慢的。这一点可以在BP神经网络的误差调整公式上看出。

事实上收敛速度逐渐减慢，这是正常的，如果一定要避免这种情况，可以自适应改变学习率。由于传统BP算法的学习速率是固定的，因此网络的收敛速度慢，需要较长的训练时间。

对于一些复杂问题，BP算法需要的训练时间可能非常长，这主要是由于学习速率太小造成的，可采用变化的学习速率或自适应的学习速率加以改进。

BP算法可以使权值收敛到某个值，但并不保证其为误差平面的全局最小值，这是因为采用梯度下降法可能产生一个局部最小值。对于这个问题，可以采用附加动量法来解决。

朱家岩隧道涌水BP网络模型分析

4.4.1神经网络模型的发展自Hebb提出的学习规则以来，人们相继提出了各种各样的学习算法。

目前，已发展了几十种神经网络，例如Hopfield模型，Feldmann等的连接型网络模型，Hinton等的玻尔茨曼机模型，以及Rumelhart等的多层感知机模型和Kohonen的自组织网络模型等等。

在这众多神经网络模型中，应用最广泛的是多层感知机神经网络。

目前，神经网络中应用最广的是前向多层神经网络的反传学习算法，即BP法，它最早是由Werbos于1974年提出来的，Rumelhart等人于1985年发展了反传网络学习算法，实现了Minsky的多层网络设想。

数学上已经证明：一个前向三层神经网络可以实现任何非线性映射，可以逼近任何复杂的函数。

4.4.2神经网络控制过程与岩溶隧道涌水过程的相似性从结构上分析，涌水过程与人工神经网络（ArtificialNetwork，简称ANN）是同构的。

涌水过程是一个非线性系统，以降雨为输入，涌水为输出，从降雨到涌水，中间要经过复杂的过程，受到地形地貌条件、地层岩性、地质结构特征及水文地质条件等多种因素的影响，各个环节形成一个相互制约、相互联结的网络结构，而人工神经网络就是一个大型非线性动力系统，各神经元分层排列并互相联结，因其联结方式的不同形成不同的网络结构，如前馈网络，反馈内层互联网络，反馈型局部联结网络等。

从概念上看，涌水机理研究就是利用观测的相关资料，分析研究涌水量等水文要素的规律，而神经网络利用观测历史数据建立系统的数学模型，识别并估计系统参数从而掌握客观水文规律。

因此，神经网络可以在一定程度上用来解决涌水机理研究的问题。

BP神经网络是人工神经网络中最为重要的网络之一，这种基于误差反传递算法的BP网络有很强的映射能力，可以解决许多实际问题，迄今为止，它的应用最为广泛。

4.4.3BP神经网络的基本原理BP神经网络是典型的多层网络，网络不仅有输入层节点、输出层节点，而且有隐含层节点。隐含层可以是一层，也可以是多层。

当信号输入时，首先传到隐含层节点，经过作用函数后，再把隐含层节点的输出信号传播到输出层节点，经过处理后给出输出结果（图4.11）。

图4.11神经网络拓扑结构示意图节点的作用函数通常选用Sigmoid型函数，其表达式为岩溶地区地下水与环境的特殊性研究网络的学习过程由正向传播和反向传播组成。

在正向传播过程中，输入信号从输入层经隐含层单元逐层处理，并传向输出层，每一层神经元的状态只影响下一层神经元的状态。

如果在输出层不能得到期望的输出，则转入反向传播，将输出信号的误差沿着原来的连接通路返回，通过修改各层神经元的权值，使得期望输出与实际输出的误差信号最小。

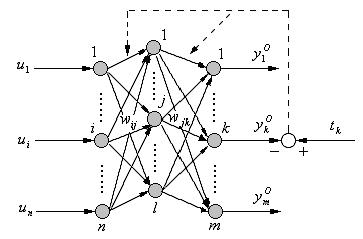
这种误差信号一般采用平方型误差函数，表达式为岩溶地区地下水与环境的特殊性研究对于只含有一层隐含层的BP网络模型来说，假设有p个样本，输入层、隐含层、输出层的神经元数分别为l，m，n；每个学习样本由输入x=（x1，x2，…，xn）及期望输出t=（t1，t2，…，tn）组成；隐含层输出为y=（y1，y2，…，ym）；输出层输出为=（，，…，）；Wij为输入层节点i到隐含层节点j的权值；Wjk为隐含层节点j到输出层节点k的权值；Hj为隐含层节点j的阈值；Hk为输出层节点k的阈值；Ek为第k个样本误差；E为总误差。

则BP网络的算法可简述如下：1）为权系数Wij、Wjk与阈值Hj和Hk设置初值，一般为较小随机数。2）将随机调用的一个学习样本（x1，x2，…，xn，t1，t2，…，tn）输入主程序。

3）求隐含层节点j的输入值netj及相应节点的输出yj，即岩溶地区地下水与环境的特殊性研究yj=f（netj）（4.20）节点的作用函数为Sigmoid型函数，岩溶地区地下水与环境的特殊性研究4）求输入层节点k的输入值netk与相应节点的输出岩溶地区地下水与环境的特殊性研究5）求输出层节点k的参考误差δk岩溶地区地下水与环境的特殊性研究6）求隐含层节点j的参考误差δj岩溶地区地下水与环境的特殊性研究7）调整隐含层节点j到输出层节点k的权值Wjk和阈值σkWjk=Wjk+η1·δk·yj，η1∈（0，1）（4.26）σk=σk+η2·δk，η2∈（0，1）（4.27）8）调整输入层节点i到隐含层节点j的权值Wij和阈值θjWij=Wij+η1·δj·xj，η1∈（0，1）（4.28）θj=θj+η2·δj，η2∈（0，1）（4.29）9）调用下一个学习样本，返回步骤（3）重复学习，直到收集的样本全部参与学习；10）计算Ek、E，使得总误差E小于某一规定的精度值，则保留权值和阈值，学习过程结束；否则转到步骤（2），重新学习，岩溶地区地下水与环境的特殊性研究岩溶地区地下水与环境的特殊性研究为了加快网络的学习速度，不导致学习产生震荡，避免结果陷入局部最小，在调整权值和阈值时加入动量项：Wij（N+1）=Wij（N）+η1·δj·xj+a·[Wij（N）-Wij（N-1）]（4.32）式中：N为迭代次数；a为动量项系数。

4.4.4隐含层神经元个数的确定隐含层起抽象的作用，即它能够从输入样本中提取特征。增加隐含层可以增加神经网络的处理能力，但是同时也会增加训练的复杂度和训练时间。

1988年Cybenko指出一个隐含层就可以实现任意判决分类问题，两个隐含层就可以表示输入图形的任意输出函数。相对于隐含层数的选择，隐含层神经元个数的选择更为复杂。

其复杂的原因在于目前为止还没有明确的方法可以计算出实际需要使用的隐含层神经元个数。所有关于隐含层神经元个数选择的建议都是基于经验的。隐含层神经元的个数少时，会造成局部极小点多，难以训练，容错性差。

而隐含层神经元个数多时又增加了网络的复杂度和训练时间，其误差也不一定最佳。Hecht-Nielsen认为在输入神经元数为N，隐含层神经元数为2N+1时，使用单隐含层的神经网络可以实现输入的任意函数。

将尝试着利用流量衰减分析和物理模拟的结果来指导隐含层神经元个数的选取。

4.4.5朱家岩隧道涌水过程的BP网络模型分析4.4.5.1研究区隧道涌水过程概化研究区地下水主要补给来源是雨水；三级台面的地表分水岭为研究区补给边界；西面隧道出口地带的渔泉溪，东面隧道进口处的干沟及南面的沿溪河流，为排泄地下水边界，分水岭补给边界与排泄边界，组成了该区水文地质单元边界条件。

三级台面为补给区，四级、五级台面为补给、径流区，排泄区不明显。研究区排泄基准面以上无隔水层存在，对排泄点不存在层制现象，所以研究区岩溶水系统类型为基控-侵蚀类型。

岩溶隧道的涌水过程极其复杂，从降雨到涌水，中间要经过蒸散发、下渗等环节，受到地形、地貌、下垫面、土壤地质以及人类活动等多种因素的影响。

我们可以将一个隧道复杂的涌水过程概化为涌水系统，该涌水系统的性能可以通过其主要影响因素体现出来，而其中物理参数的次要特性以及物理参数精度的空间分布可以忽略，从而使问题得以简化。

BP神经网络是一个非线形系统，可以用于逼近非线形映射关系，也可以用于逼近一个极为复杂的函数关系。

对于研究区岩溶管道水系统来说，其一定时段内的水量平衡方程如下：Q=P-E±ΔS（4.33）式中：Q为隧道涌水量；P为降水量；E为蒸散发量；ΔS为地下水储量的变化量。

即可得出：Q=f（P，E，ΔS）（4.34）这是一个非常复杂的映射关系，可以将之概化为一个系统，利用BP神经网络，对之进行模拟逼近。如前所述，从结构上来说，BP神经网络与隧道涌水系统是同构的。

接下来，利用朱家岩隧道岩溶管道结构和BP神经网络结构进行类比分析，从而建立模型。

4.4.5.2朱家岩隧道岩溶管道涌水的BP网络模型研究（1）训练样本资料准备神经网络岩溶管道涌水模型分为系统识别与模型应用两个阶段：前者精选已知的实测资料作为样本来训练网络识别参数，后者则应用训练好的网络分析得到径流模拟值。

一定时段内隧道的涌水量Q与该区域上的降雨量、蒸散发量以及地下水储量的变化量有关，而其中地下水储量的变化量与区域前期影响雨量以及本时段的降水量和蒸散发量有关，所以该变化量可以表示为该时段以及先前时段的降水量及蒸散发量的函数，故而可以进一步将Q表示为该时段及先前时段P、E的函数。

在实际研究中，P通常为实测值，E因为主要与温度、日照时间、云量和湿度有关，所以E通常用温度、湿度等量值来计算，因此，可以用一个系统来概化Q与前面提及的影响因素之间的复杂关系，建立系统模型。

本次模型参数识别、训练采用了2005年4月29日～2005年11月25日宜昌气象局日平均气温、日照时数和降雨量作为输入资料，朱家岩隧道的涌水量作为输出资料进行分析研究，其中将4月29日～7月9日、7月24日～11月25日共166组数据作为训练样本进行训练学习，7月10日～7月23日的数据作为检验样本用于对训练成功的网络进行预测检验。

图4.12为2005年4月29日～2005年11月25日总共180d的日降雨量（mm）、宜昌气象局日平均气温（℃）和日照时数（h）以及涌水量（m3/d）。

岩溶地区地下水与环境的特殊性研究岩溶地区地下水与环境的特殊性研究岩溶地区地下水与环境的特殊性研究图4.12研究区涌水量、平均气温、日照时数和降水量图（2）样本数据的预处理由于BP网络的输入层物理量及数值相差甚远，为了加快网络收敛的速度，在训练之前须将各输入物理量进行预处理。

数据的预处理方法主要有标准化法、重新定标法、变换法和比例放缩法等等。

本研究所选用的是一种最常用的比例压缩法[4]，公式如下：岩溶地区地下水与环境的特殊性研究式中：X为原始数据；Xmax、Xmin为原始数据的最大值和最小值；T为变换后的数据，也称之为目标数据；Tmax、Tmin为目标数据的最大值和最小值。

由于Sigmoid函数在值域[0，0.1]和[0.9，1.0]区域内曲线变化极为平坦，因此合适的数据处理是将各输入物理量归至[0.1，0.9]之间。

将每个样本输入层的6个物理量进行归一化处理：岩溶地区地下水与环境的特殊性研究BP网络的算法对训练样本的顺序有很强的敏感性，按随机数随机排列样本的次序，有助于加快网络训练的速度。

（3）网络训练与模拟已经将输入样本的个数定为6个，但是对于隐含层神经元个数的选择，到目前为止还没有明确的方法可以计算出实际需要使用的隐含层神经元个数，在选择时通常是采用试算的方法[5]。

虽然现今的BP神经网络还是一个黑箱模型，其参数没有水文物理意义[6]，但从结构上分析，涌水过程与ANN是同构的。

对于一个岩溶地下水系统，在一次降水之后，水流通过下渗进入到地下，经过多个裂隙、溶隙、管道，最后汇集到突水点，在这过程中，各个裂隙、溶隙、管道都有其相应的蓄水容量等阈值，而降水是其输入，涌水量是其输出，这类似于人工神经元模型中的阈值、激活值、输出等器件。

研究区域管道发育程度有三个级别，在一次降水之后，地下水流经过3条岩溶通道（裂隙、溶隙、管道）的蓄积后在隧道经过涌水排出，这一过程可以与BP神经网络结构进行类比，其中3条岩溶通道（裂隙、溶隙、管道）相当于隐含层中的3个神经元，各通道的蓄水容量相当于隐含层中人工神经元的阈值，涌水量相当于输出值，从整体上来说，BP神经网络的结构已经灰箱化。

在以上类比的设想下，将隐含层中的神经元个数定为3个，采用6-3-1的网络结构（表4.5；图4.13）。

图4.13BP网络模型示意图表4.5BP网络模型参数一览表定义系统目标精度为0.0005，误差公式是对训练出网络的输出层节点和实际的网络输出结果求平方差的和。

最大训练次数取5000次，如果到达最大训练次数网络还未达到目标精度，程序退出。已经确定网络的输入层神经元数目为6，隐含层神经元数目为3，输出层神经元数目为1。训练算法选取附加动量法。

激活函数选取Sigmoid。程序执行5000次后BP网络模型训练成功。网络映射值与实测值的相关关系见图4.14。

图4.14网络映射值与实测值相关关系将用来检验的7月10～23日的数据作为输入层数据输入已经训练好的BP网络模型，然后将其输出值与同期的实测资料进行对比，其分析结果见图4.15。

图4.15涌水量实测值与BP网络计算值比较从图4.15可以看出，用BP网络模拟的涌水量中，7月10日～7月23日中涌水量变化大体一致，模拟情况较好，证明了流量衰减分析和物理模拟结果的可靠性。

应用确定性系数分析方法对模型精度进行评定，确定性系数dy表达式如下：dy=1-S2/σ2（4.37）岩溶地区地下水与环境的特殊性研究岩溶地区地下水与环境的特殊性研究式中：S为模型计算值与实测值之差的均方差；σ为实测值的均方差；yi为实测值；y为模型计算值；为实测值的均值；n为检验样本数。

dy值越大，表明模型计算精度越高。经计算，基于BP网络的朱家岩隧道涌水模型的确定性系数为0.9805，符合模型精度要求。将此降水量值输入已经检验好的BP网络模型，求得最大涌水量为12850m3/d。

用matlab实现bp算法，对样本进行训练

。

P=[5.7003.8000.31752.33;4.5503.0500.31752.33;2.9501.9500.31752.33;1.9501.3000.31752.33;1.4000.9000.31752.33;1.2000.8000.31752.33;1.0500.7000.31752.33;1.7001.1000.95252.33;1.7001.1000.15242.33;4.1004.1400.15242.50;10.804.1400.15242.50;0.8501.2900.01702.22;2.0002.5000.07902.22;1.0631.1830.07902.55;0.9101.0000.127010.2;1.7201.8600.15702.33;1.2701.3500.16302.55;1.5001.6210.16302.55;1.1201.2000.24202.55;1.4031.4850.25202.55;1.5301.6300.30002.50;0.9051.0180.30002.50;1.1701.2800.30002.50;0.7761.0800.33002.55;0.7901.2550.40002.55;0.9871.4500.45002.55;0.8141.4400.47602.55;0.9701.6200.55002.55;1.2001.9700.62602.55;0.7832.3000.85402.55;0.9742.6200.95202.55;1.0202.6400.95202.55;0.8832.6761.00002.55;0.7772.8351.10002.55;0.9203.1301.20002.55;1.2653.5001.28102.55;1.0803.4001.28102.55];%输入T=[2310;2890;4240;5840;7700;8270;9140;4730;7870;2228;2181;7740;3970;7730;4600;5060;6560;5600;7050;5800;5270;7990;6570;8000;7134;6070;6380;5990;46604600;3980;3900;3980;3900;3470;2980;3150];%输出P=P';T=T';%创建一个新的前向神经网络net_1=newff(minmax(P),[10,1],{'tansig','purelin'},'traingdm');%当前输入层权值和阈值{1,1}inputbias=net_1.b{1}%当前网络层权值和阈值{2,1}layerbias=net_1.b{2}%设置训练参数=NaN;=0.05;=0.9;net_1.trainParam.epochs=10000;=1e-6;%调用TRAINGDM算法训练BP网络[net_1,tr]=train(net_1,P,T)。

BP神经网络中动量项系数怎么定？

trainbpx有动量法和自适应调整学习率的特点，能有效减小震荡趋势改善收敛性、抑制网络陷入局部极小值。

在用动量法对网络训练之前，首先应将网络权值和阈值的修正值矩阵初始化为零矩阵，然后利用函数learnbpm求得修正值矩阵。

基于改进的BP人工神经网络算法的软土地基沉降预测

改进的BP神经网络预测需要等间隔数据，利用Spline插值点进行建模。

为了和前述方法的预测效果对比，仍选取550～665d（共24个样本数据）的沉降量作为训练样本，预留670～745d（共16个样本数据）的沉降量作为对训练好的BP人工神经网络的检验样本。

以每相邻的连续4个沉降量（时间间隔Δt=5d）作为一个输入样本（S1，S2，S3，S4），紧邻的第5个沉降量作为目标样本（S5），这样，利用24个原始数据点，构建了21组训练样本输入向量。

每组训练样本的输入层单元数为n=4，输出层单元数为q=1，又隐层单元数p的确定公式为温州浅滩软土工程特性及固结沉降规律研究式中：a为1～10之间的常数。由式（5.57）确定隐层神经元数为p=3～12。

其具体值将通过BP人工神经网络训练误差来判断，取网络误差最小时对应的隐层神经元数。

本书基于MATLAB7.1编制了改进的BP神经网络程序，对标准的BP人工神经网络算法采取了增加动量项法和自适应调节学习速率法两点改进，此外，对输入输出数据进行了尺度变换（归一化处理），变换后可防止因净输入的绝对值过大而使神经元输出饱和，继而使权值调整进入误差曲面的平坦区。

输入输出数据变换为[0，1]区间内的值的归一化预处理变换式为温州浅滩软土工程特性及固结沉降规律研究式中：xi为输入或输出数据；xmin、xmax为最值；为输入或输出数据的归一化值。

BP神经网络模型的训练曲线如图5.17所示。本书所建立的改进的BP神经网络模型之拟合/预测值与实测值列于表5.13，拟合/预测曲线与实测曲线对比如图5.18所示，其残差图如图5.19所示。

由表5.13和图5.18、5.19可知，改进的BP神经网络模型预测结果的平均残差为0.1cm，平均相对误差为0.06%，拟合及预测效果很好。

但是与前面几种预测方法不同的是，改进的BP人工神经网络模型的预测值略小于实测值，随着预测时间远离训练样本，这将使结果偏于不安全，所以，建议该法用于短、中期预测。

同时，为了使后期预测精度更高，应不断更新训练样本向量集。

图5.17N5+850断面BP神经网络训练曲线图5.18N5+850断面改进的BP人工神经网络模型预测曲线与实测曲线对比图5.19N5+850断面改进的BP人工神经网络模型预测残差图表5.13改进的BP神经网络预测值与实测值对比。

BP神经网络动量因子不理解

BP神经网络在批处理训练时会陷入局部最小，也就是说误差能基本不变化其返回的信号对权值调整很小但是总误差能又大于训练结果设定的总误差能条件。

这个时候加入一个动量因子有助于其反馈的误差信号使神经元的权值重新振荡起来。可以参看一些专门介绍神经网络的书籍。