机器学习之期望最大算法
导读
EM算法,全称Expectation Maximization Algorithm,期望最大算法是一种迭代算法,用于含有隐变量(Hidden Variable)的概率参数模型的最大似然估计或极大后验概率估计。
思想
EM 算法的核心思想非常简单,分为两步:Expection-Step和Maximization-Step。E-Step主要通过观察数据和现有模型来估计参数,然后用这个估计的参数值来计算似然函数的期望值;而M-Step是寻找似然函数最大化时对应的参数。由于算法会保证在每次迭代之后似然函数都会增加,所以函数最终会收敛。
算法流程
输入:观察数据 x = ( x ( 1 ) , x ( 2 ) , … , x ( m ) x = (x^{(1)}, x^{(2)},\dots,x^{(m)} x=(x(1),x(2),…,x(m),联合分布 p ( x , z ∣ θ ) p(x,z|\theta) p(x,z∣θ),条件分布p(z|x,\theta),极大值迭代次数J。
- 随机初始化模型参数 θ \theta θ的初值 θ ( 0 ) \theta^{(0)} θ(0);
- for j from 1 to J:
- E步:计算联合分布的条件概率期望:
Q i ( z ( i ) ) : = P ( z ( i ) ∣ x ( i ) , θ ) Q_{i}(z^{(i)}) := P(z^{(i)}|x^{(i)},\theta) Qi(z(i)):=P(z(i)∣x(i),θ) - M步:极大化 L ( θ ) L(\theta) L(θ),得到 θ \theta θ:
θ : = a r g m a x θ ∑ i = 1 m ∑ z ( i ) Q i ( z ( i ) ) l o g P ( x ( i ) , z ( i ) ∣ θ ) \theta := argmax_{\theta} \sum_{i=1}^{m}\sum_{z^{(i)}} Q_{i}(z^{(i)}) log P(x^{(i)}, z^{(i)}|\theta) θ:=argmaxθi=1∑mz(i)∑Qi(z(i))logP(x(i),z(i)∣θ)
- E步:计算联合分布的条件概率期望:
重复E、M步骤直到 θ \theta θ收敛
例子
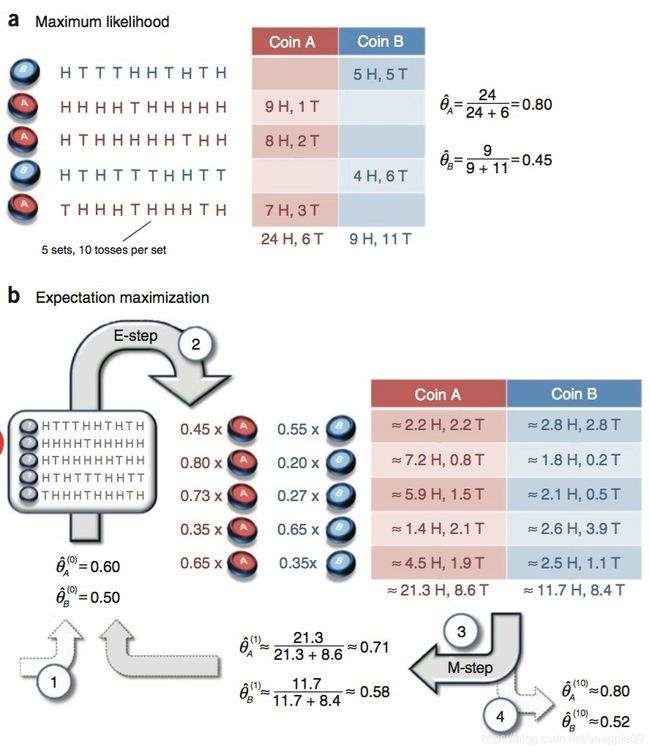
假设有两枚硬币 A 和 B,他们的随机抛掷的结果如下图所示:
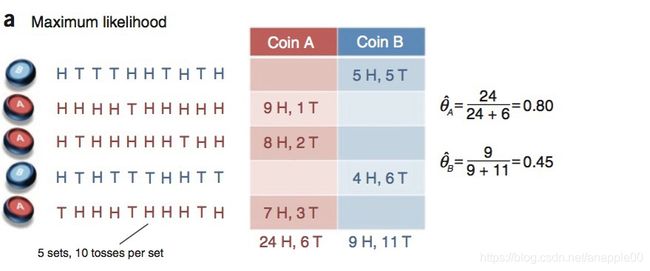
我们很容易计算出两枚硬币抛出正面的概率(即概率分布),硬币A正面的概率为:
θ A = 24 30 = 0.8 \theta_{A} = \frac{24}{30} = 0.8 θA=3024=0.8
硬币B正面的概率为:
θ B = 9 20 = 0.45 \theta_{B} = \frac{9}{20} = 0.45 θB=209=0.45
现在我们加入隐变量,抹去每轮投掷的硬币标记:
| coin | Statistics |
|---|---|
| Coin* | 5H, 5T |
| Coin* | 9H, 1T |
| Coin* | 8H, 2T |
| Coin* | 4H, 6T |
| Coin* | 7H, 3T |
现在我们不知道每次投的硬币是哪一个,我们想求一下这5次投的硬币序列: Z = { z 1 , z 2 , z 3 , z 4 , z 5 } Z = \{z_{1},z_{2},z_{3},z_{4},z_{5}\} Z={z1,z2,z3,z4,z5}
碰到这种情况,我们该如何估计 θ A \theta_{A} θA和 θ B \theta_{B} θB的值?
我们多了一个隐变量 Z = { z 1 , z 2 , z 3 , z 4 , z 5 } Z = \{z_{1},z_{2},z_{3},z_{4},z_{5}\} Z={z1,z2,z3,z4,z5},代表每一轮所使用的硬币,我们需要知道每一轮抛掷所使用的硬币这样才能估计 θ A \theta_{A} θA和 θ B \theta_{B} θB的值,但是估计隐变量Z我们又需要知道 θ A \theta_{A} θA和 θ B \theta_{B} θB的值,才能用极大似然估计法去估计出 Z。这就陷入了一个鸡生蛋和蛋生鸡的问题。
其解决方法就是先随机初始化 θ A \theta_{A} θA和 θ B \theta_{B} θB,然后用去估计 Z, 然后基于 Z 按照最大似然概率去估计新的 θ A \theta_{A} θA和 θ B \theta_{B} θB,循环至收敛。
计算
E步:初始化 θ ^ A ( 0 ) = 0.60 \hat{\theta}_{A}^{(0)} = 0.60 θ^A(0)=0.60和 θ ^ B ( 0 ) = 0.50 \hat{\theta}_{B}^{(0)} = 0.50 θ^B(0)=0.50,并计算每个实验中选择的硬币是A还是B的概率,例如第一轮的结果:“H T T T H H T H T H”,即5H 5T,当选择硬币A时抛出这个结果的概率为:
P ( z = A ∣ y 1 , θ ) = P ( z = A , y 1 ∣ θ ) P ( z = A , y 1 ∣ θ ) + P ( z = B , y 1 ∣ θ ) = ( 0.6 ) 5 × ( 0.4 ) 5 ( 0.6 ) 5 × ( 0.4 ) 5 + ( 0.5 ) 5 × ( 0.5 ) 5 = 0.45 P(z=A|y_{1},\theta) = \frac{P(z = A,y_{1}|\theta)}{P(z = A,y_{1}|\theta) + P(z = B,y_{1}|\theta)} = \frac{(0.6)^{5} \times (0.4)^{5}}{(0.6)^{5} \times (0.4)^{5} + (0.5)^{5} \times (0.5)^{5}} = 0.45 P(z=A∣y1,θ)=P(z=A,y1∣θ)+P(z=B,y1∣θ)P(z=A,y1∣θ)=(0.6)5×(0.4)5+(0.5)5×(0.5)5(0.6)5×(0.4)5=0.45
当选择硬币B时抛出这个结果的概率为:
P ( z = B ∣ y 1 , θ ) = 1 − P ( z = A ∣ y 1 , θ ) = 0.55 P(z=B|y_{1},\theta) = 1 - P(z=A|y_{1},\theta) = 0.55 P(z=B∣y1,θ)=1−P(z=A∣y1,θ)=0.55
按这种方法计算5次投掷使用硬币A和硬币B的概率分别为:
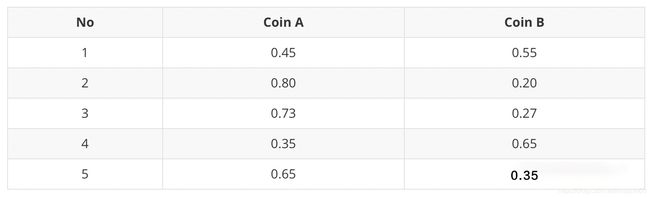
M步:
结合上面计算出的硬币A和硬币B的概率和50次投掷结果,我们利用期望分别求出硬币A和硬币B对投掷结果的贡献。例如第一轮的结果:“H T T T H H T H T H”,即5H 5T,硬币A对此的贡献为,正面: 0.45 × 5 = 2.25 0.45 \times 5 = 2.25 0.45×5=2.25(5代表正面是5次);反面: 0.45 × 5 = 2.75 0.45 \times 5 = 2.75 0.45×5=2.75(5代表反面是5次);第二轮结果:“H H H H T H H H H H”,即9H 1T,硬币A对此的贡献为:正面: 0.8 × 9 = 2.25 0.8 \times 9 = 2.25 0.8×9=2.25(9代表正面是9次);反面: 0.8 × 1 = 2.75 0.8 \times 1 = 2.75 0.8×1=2.75(1代表反面是1次),以此类推。于是我们可以得到:
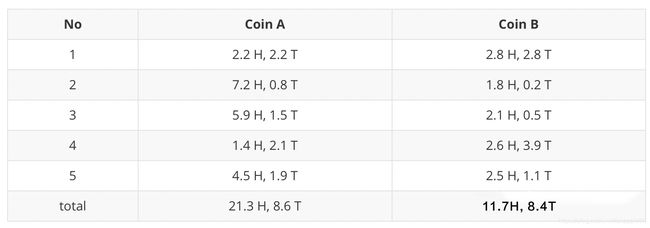
把硬币A对这5次投掷正反面的贡献都计算出来之后求和:
正 面 贡 献 : 21.3 反 面 贡 献 : 8.6 正面贡献:21.3\\ 反面贡献:8.6 正面贡献:21.3反面贡献:8.6
更新 θ A \theta_{A} θA:
θ ^ A ( 1 ) = 21.3 21.3 + 8.6 = 0.71 \hat{\theta}_{A}^{(1)} = \frac{21.3}{21.3 + 8.6} = 0.71 θ^A(1)=21.3+8.621.3=0.71
同理更新 θ B \theta_{B} θB:
θ ^ B ( 1 ) = 11.7 11.7 + 8.4 = 0.58 \hat{\theta}_{B}^{(1)} = \frac{11.7}{11.7 + 8.4} = 0.58 θ^B(1)=11.7+8.411.7=0.58
至此重新估计出了参数值。如此反复迭代,我们就可以算出最终的参数值。
总结
- 参数
$ \theta $(Model Parameters):中心点的坐标$ \theta = \{\mu_{1},\mu_{2}...\mu_{k}\} $ - 参数
$ \gamma $(Latent Variables):隐含状态参量,即每 个点属于哪个类别
损失函数(最小化目标minimize):
l ( θ ) = ∑ i = 1 n ∑ k = 1 k γ i k ∣ ∣ x i − μ k ∣ ∣ 2 2 l(\theta) = \sum_{i=1}^{n} \sum_{k=1}^{k} \gamma_{ik}||x_{i} - \mu_{k}||_{2}^{2} l(θ)=i=1∑nk=1∑kγik∣∣xi−μk∣∣22
计算过程(参照EM算法,交替优化):
- E-step:随机初始化中心点(固定中心点 θ \theta θ), 找出每个点属于哪个类别,即找出距离每个点最近的中心点,并把该点标记为那个类别,得到 γ \gamma γ
- M-step:更新参数 θ \theta θ,即更新隐含状态中心点,对于所有类别属于 k k k的点来说,计算它们的中心,得到了那个类别的中心点 μ k \mu_{k} μk
- E-step和M-step循环