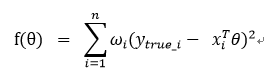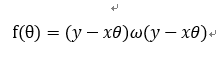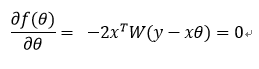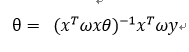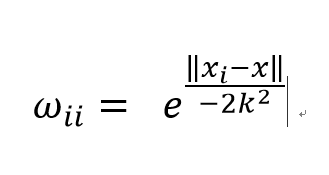局部加权线性回归算法(Locally Weighted Linear Regression)及相关案例

局部加权线性回归算法(Locally Weighted Linear Regression)及相关案例

大家好，我是W

这次讲线性回归，之前有说逻辑回归（Logistic Regression），虽然逻辑回归负责分类，可是在数据到达二值函数之前的逻辑都是线性回归的逻辑，所以这两个回归是十分相似的。这篇文章的顺序是：1、线性回归算法原理 2、最小二乘法和算法评估标准 3、案例1-简单数据集标准线性回归 4、案例2-简单数据集局部加权线性回归 5、案例3-鲍鱼年龄预测。

案例2-简单数据集局部加权线性回归

接上一篇内容，之前使用标准线性回归还有欠拟合情况，那么存在一种局部加权的线性回归，其原理到底怎么样的?

案例2-局部加权线性回归原理

标准线性回归模型是一种无偏差估计，在计算所有点的时候都是无偏差地计算误差并且优化误差。这按道理来说没什么不好，但是会出现欠拟合的现象，即模型的优化是根据整体训练集的样本来优化的，考虑得过于整体，没办法针对不同的点来做相应的调整。

所以可以引入局部加权线性回归来改善欠拟合的现象。局部加权线性回归的思想是希望使用离待拟合样本较近的样本来描述。类似于质量相等的天体间的万有引力，距离越近引力越大。当对样本x_i预测目标值y_predict的时候，我们需要计算权重W，W权重由x_i周围的点来决定。

假设我们要预测x_i的目标值y_predict，我们需要得到第i个样本对应的w_i权重矩阵，那么损失函数变为（为区分权重矩阵跟回归系数，现改符号权重矩阵为W，回归系数为θ）：

用矩阵形式表示：

对θ求偏导并等于0（注意这里因为是矩阵表示，w表示某个样本i的权重矩阵，W表示全部样本的权重矩阵）：

即：

即：

最终可得θ：

经过上面这些步骤可以看出，只要知道W权重矩阵，那么剩下的跟标准线性回归求回归系数θ没有差别，那么W权重矩阵怎么求？

案例2-W权重矩阵求解

求解W权重矩阵需要使用到核函数，因为我们希望得到的是类似万有引力的效果（即距离越近权重越大引力越强），所以使用核函数来对附近的点赋予更高的权重，通常使用的是高斯核函数，形式如下：

通过高斯核函数，可以看出有几个性质。

• 若x_i离x近，则w_ii大，反之小。
• 参数k决定权重大小，k越大，权重差距越小，k越小，权重差距越大。
• 当k趋于无穷大，所有的权重趋于1，W权重矩阵趋于单位矩阵，整个模型趋于标准线性回归模型。

案例2-原理总结

因为标准线性回归模型存在一定的缺陷（欠拟合），所以基于希望使用离待拟合样本较近的样本来描述的思想，我们给每一个回归系数做一个权重矩阵，从而使得每个测试样本跟周围的训练样本更拟合。而权重矩阵使用的是高斯核。

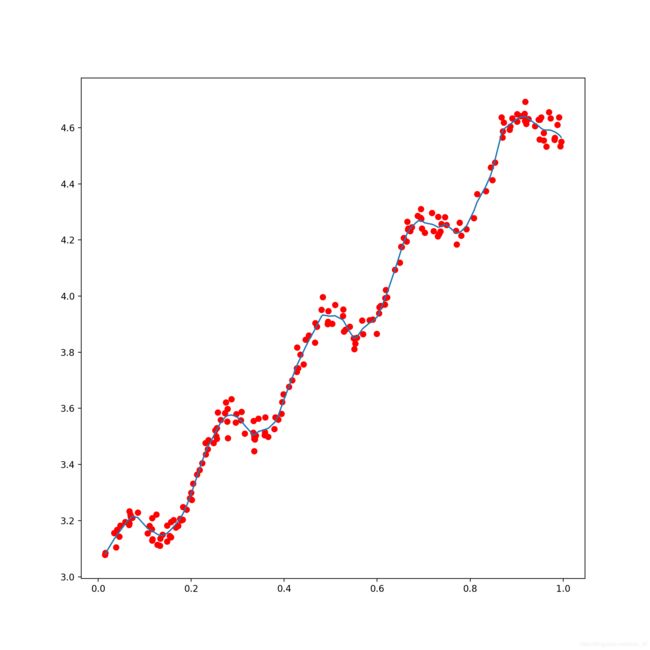
案例2-查看数据集

没错，使用的还是案例1的数据集。这个螺旋上升的数据集可以很清晰的看出两种回归的差别。

print(df)

      x0        x1         y
0    1.0  0.427810  3.816464
1    1.0  0.995731  4.550095
2    1.0  0.738336  4.256571
3    1.0  0.981083  4.560815
4    1.0  0.526171  3.929515
..   ...       ...       ...
194  1.0  0.257017  3.585821
195  1.0  0.833735  4.374394
196  1.0  0.070095  3.213817
197  1.0  0.527070  3.952681
198  1.0  0.116163  3.129283

案例2-读取数据

略，同案例1

案例2-局部加权

由于经过原理分析，我们知道针对不同的数据样本，需要根据邻近的点来计算权重矩阵，从而计算出每个待预测样本的回归系数。所以，我们需要对待测样本进行遍历。对每个待测样本计算出其对应的权重矩阵。

def lwlr_predict(test_matrix, data_matrix, label_matrix, k=0.5):
    """
    调用局部加权线性回归
    通过遍历对每一个实例调用局部加权线性回归函数来得到对应预测值
    :param test_matrix:
    :param data_matrix:
    :param label_matrix:
    :param k:
    :return:
    """
    y_predict = np.zeros(len(data_matrix))
    # print(y_predict)
    for i in range(len(data_matrix)):
        y_predict[i] = lwlr(test_matrix[i], data_matrix, label_matrix, k)

    # 返回估计值
    return y_predict

接下来是核心：

def lwlr(testPoint, data_matrix, label_matrix, k=0.5):
    # [n,n]的单位阵
    weights = np.mat(np.eye(len(data_matrix)))
    # 这个循环把单位阵上对角线元素全部更新成核函数计算出来的值
    # 循环即计算权重矩阵的过程 每一个测试样本预测都需要生成对应的权重矩阵
    for i in range(len(data_matrix)):
        # 计算该实例与其他点的距离
        distance_vector = testPoint - data_matrix[i, :]
        # print("distance shape", np.shape(distance_vector))
        # print("testPoint:", testPoint)
        # print("data_i:", data_matrix[i, :])
        # print("distance:", distance_matrix)
        weights[i, i] = np.exp(distance_vector * distance_vector.T / (-2.0 * k ** 2))
    # 此时的weights对角线上全是对每一维的权重
    xTx = data_matrix.T * (weights * data_matrix)
    if linalg.det(xTx) == 0:
        print("行列式为0")
        return

    # print(np.shape(xTx))
    # print(np.shape(data_matrix.T))
    # print(np.shape(label_matrix))
    # 这里可以看出回归系数是每一个点都不同的 因为每个点都要算一个weights权重矩阵
    w = xTx.I * (data_matrix.T * (weights * label_matrix))
    return testPoint * w

案例2-画图

def my_draw(data_matrix, label_matrix, y_predict):
    fig = plt.figure(figsize=(10, 10), dpi=200)
    sorted_index = data_matrix[:, 1].argsort(0)
    x_sorted = data_matrix[sorted_index][:, 0, :]
    # print(x_sorted)

    plt.plot(x_sorted[:, 1], y_predict[sorted_index])
    plt.scatter(x=data_matrix[:, 1].flatten().A[0], y=label_matrix.T.flatten().A[0], c='red')
    plt.savefig("./dataSet/2.png")

案例3-鲍鱼年龄预测

鲍鱼年龄预测是一个真实的应用场景，数据集来自UCI，数据集中记录了鲍鱼样本的各项指标及其壳的层数（通过层数可以知道鲍鱼年龄）。这个数据集会随项目放在GitHub上。

开发流程：

• 收集数据： UCI找到相关数据集。
• 准备数据： 数据集中可能会出现标称型数据，需要将其转为二值型数据。
• 分析数据： 通过作图等方式从各角度去分析数据。
• 训练算法： 找到回归系数。
• 测试算法： 通过mse，rss等指标来计算误差大小，分析模型效果。
• 使用算法： 使用样本数据来做预测。

案例3-查看数据集

Sex,Length,Diameter,Height,Whole weight,Shucked weight,Viscera weight,Shell weight,Rings
M,0.455,0.365,0.095,0.514,0.2245,0.101,0.15,15
M,0.35,0.265,0.09,0.2255,0.0995,0.0485,0.07,7
F,0.53,0.42,0.135,0.677,0.2565,0.1415,0.21,9
M,0.44,0.365,0.125,0.516,0.2155,0.114,0.155,10
I,0.33,0.255,0.08,0.205,0.0895,0.0395,0.055,7
I,0.425,0.3,0.095,0.3515,0.141,0.0775,0.12,8
F,0.53,0.415,0.15,0.7775,0.237,0.1415,0.33,20
F,0.545,0.425,0.125,0.768,0.294,0.1495,0.26,16
M,0.475,0.37,0.125,0.5095,0.2165,0.1125,0.165,9
F,0.55,0.44,0.15,0.8945,0.3145,0.151,0.32,19
F,0.525,0.38,0.14,0.6065,0.194,0.1475,0.21,14
M,0.43,0.35,0.11,0.406,0.1675,0.081,0.135,10
M,0.49,0.38,0.135,0.5415,0.2175,0.095,0.19,11
F,0.535,0.405,0.145,0.6845,0.2725,0.171,0.205,10

可以看到该数据集包含了8个特征和一个目标值Rings，所以很明显我们需要预测鲍鱼的年轮。还可以看到数据集中有一个特征属于标称型数据-Sex，显然在这个特征上我们需要做相应的处理。

值得注意的是，这个数据集比以往的数据集大了不少，达到4177个数据样本，在后期实际训练中我出现了训练时间过长的问题（可能是因为算法复杂度较高的原因吧）。

案例3-加载数据集和处理标称型数据

首先，加载数据集跟以往的方法一样，通过pandas读取csv文件即可，同样把数据集划分为特征集和目标值。并且因为训练过程中出现训练时间过长的问题，所以我决定先截取前200个样本做训练。

def load_data(file_path):
    """
    针对鲍鱼数据集做数据加载 需要把标称数据转为二值型数据
    :param file_path: 路径
    :return:
    """
    df = pd.read_csv(file_path)
    # 取前一百条数据训练 否则太久了
    df = df[:100]

    data_matrix = np.mat(df.iloc[:, :-1])
    # [n,1]
    label_matrix = np.mat(df.iloc[:, -1]).T

    return data_matrix, label_matrix

但是我们还要把标称型数据转为one-hot，这里使用的是pandas的get_dummies函数。这个函数可以将指定的特征向量的不同值作为新特征矩阵的列，如此一来就能转为one-hot矩阵，若还有疑问请看下面的打印。

print(Sex)
# 可以看到Sex特征向量有三个不同值，分别是I、M、F
0     M
1     M
2     F
3     M
4     I
     ..
95    M
96    M
97    M
98    M
99    F

那么get_dummies是怎么做的呢？对这个向量内容去重，得到I、M、F，然后分别做成3个特征列：

    F  I  M
0   0  0  1
1   0  0  1
2   1  0  0
3   0  0  1
4   0  1  0
.. .. .. ..
95  0  0  1
96  0  0  1
97  0  0  1
98  0  0  1
99  1  0  0

分别在对应的值下面打1，那么就可以转为one-hot矩阵了。

最终读取和处理标称型数据的代码：

def load_data(file_path):
    """
    针对鲍鱼数据集做数据加载 需要把标称数据转为二值型数据
    :param file_path: 路径
    :return:
    """
    df = pd.read_csv(file_path)
    # 取前一百条数据训练 否则太久了
    df = df[:100]
    # 把sex改为 F I M 三列
    sex_array = df["Sex"]
    data_transformed = rearrange_nominal_data(sex_array)
    df["F"] = data_transformed["F"]
    df["I"] = data_transformed["I"]
    df["M"] = data_transformed["M"]
    # 删除原来的Sex
    df.drop(labels="Sex", axis=1, inplace=True)

    # 把Rings维持在最后一列
    tmp_array = df["Rings"]
    df.drop(labels="Rings", axis=1, inplace=True)
    df["Rings"] = tmp_array

    data_matrix = np.mat(df.iloc[:, :-1])
    # [n,1]
    label_matrix = np.mat(df.iloc[:, -1]).T

    return data_matrix, label_matrix


def rearrange_nominal_data(feature_array):
    data_transformed = pd.get_dummies(feature_array)
    return data_transformed

案例3-程序整体逻辑

说白了就是main函数，给大家看一下整体需要做的工作才能更好地理解。

if __name__ == '__main__':
    # 加载数据
    file_path = "./dataSet/abalone.csv"
    data_matrix, label_matrix = load_data(file_path)
    print(data_matrix)
    for i in [1, 5, 10]:
        print("第%d轮" % i)
        # 得到估计值y_predict
        y_predict = lwlr_predict(data_matrix, data_matrix, label_matrix, i)
        # 画图
        my_draw(data_matrix, label_matrix, y_predict, i)
        # 计算rss mse
        rss = cal_rss(y_predict, label_matrix)
        mse = cal_mse(y_predict, label_matrix)
        print("第%d个核的rss:%f" % (i, rss))
        print("第%d个核的mse:%f" % (i, mse))

在读取完数据之后就是循环，而这个循环的目的是为了替换高斯核的k值，从而查看不同的拟合效果。剩下的步骤就与案例2一样了。

参考

• 线性回归，加权回归，推导过程
• 机器学习算法实践-标准与局部加权线性回归
• 机器学习（1）------ 线性回归、加权线性回归及岭回归的原理和公式推导

项目地址

点击进入github