【机器学习原理】SVM支持向量机分类算法

一、支持向量机：线性分类器的“王者”

• 最大间隔
• 高维映射
• 核方法

1. 距离

我们已经从用线性回归套S型马甲（logistic回归）、物以类聚（K近邻）、统计（朴素贝叶斯）和if-else（决策树）等角度思考了分类问题。
回想一下就知道，对数据点的分类实际并不涉及任何“移动”操作，原因也不难想见。数据点的“位置”实质是在不同维度有着不同现实含义的信息，我们当然不可能为了分类而改变这些信息的值。
譬如很常见的中国象棋，我们知道棋子分为红色和黑色两种，开局都要整整齐齐地排列在棋盘上。棋盘中央有一道“楚河汉界”，正好把这两种不同颜色的棋子分开。如果我们的任务是画一条直线把不同颜色的棋子分类，显然轻而易举。既然楚河汉界是红黑两种棋子之间的分割地带，只要找到这条空白地带，然后沿着其中轴画一条线，就一定能把两类棋子分开。
能够对当前数据点进行正确分隔的直线有许多，可是选择哪条最好呢？也许我们本能地就会选择沿中轴画线，可是为什么呢？我们中国人做事都是讲究留有余地的，数据分类也是如此。虽然棋盘上的棋子摆得整齐，但我们说过，自然中的数据可是会随机波动的，如果分隔线不留余地，那么它将对噪声非常敏感。数据出现一点点扰动泛化则误差会变得很大，无法有效进行正确分类，学术上称“鲁棒性很差”。那么怎么提高鲁棒性呢？也很简单，即尽可能地多留点儿余地，而且是要给正负类两边都多留点，使得分割线距离两边都达到最大间隔。

2. 支持向量

支持向量机是一种机器学习算法，其中涉及一个很重要的角色叫“支持向量”，这也是该算法的名字由来。

支持向量机还有一个重要概念叫“间隔（margin）”。回顾刚才的分类，我们的目的是要把两堆不同类的棋子用一条直线隔开，而对这条直线我们也有要求，就是要距离最远。不过，这条空白地带怎么找呢？我们可以俯视整个棋盘，可机器只能进行数值计算，没有这种几何成像能力，必须得先数值化了才能运作。不过好办，我们知道，红色棋子和黑色棋子之间既然有空白地带，那就说明棋子与棋子之间有距离。不过这也有讲究，红色的棋子距离黑色棋子有远有近，就拿黑色的“卒”作为参照物吧，红色的“兵”肯定是离它最近的，而相比之下，红色的“帅”则要远很多。这就是间隔。不难想象，在任何分类任务中，只要找到两种不同的类之间的间隔，就能把两个类分开。如图8-1所示。

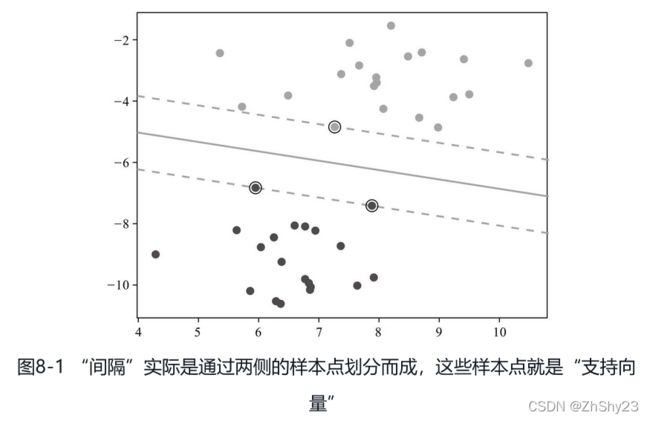
让间隔最大化，或者形象一点，让间隔变得“最胖”，就是支持向量机的目标。间隔分为两种，一种叫硬间隔，一种叫软间隔。特别顽固、一点也不通融的是硬间隔，知道会有划错但希望尽可能少的则是软间隔。

3. 从更高维度看“线性不可分”

高维映射是支持向量机最让人注目的部分，也是数学在机器学习算法里能够达到的巅峰。数学上有一种思路，即遇到新的难题时通常分两步解决。第一步，将新问题转化成已经解决的旧问题；第二步，完成转化后，通过老方法加以解决。我们要解决的问题就是，怎样将线性不可分变得线性可分，然后再按老办法寻找最大间隔。

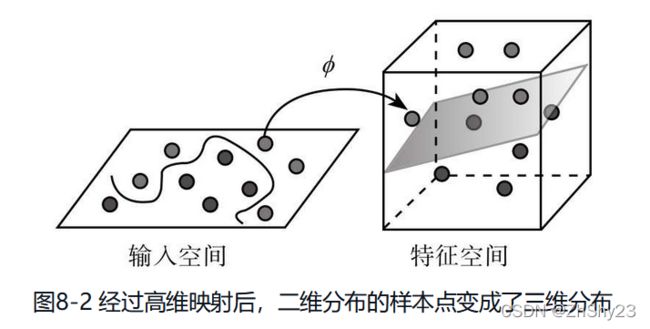
让线性不可分变为线性可分，这不是矛盾吗？不矛盾。线性不可分只是在当前的维度下线性不可分，但如果增加了维度，原本不可分也就可分了。还是以刚才的围棋为例，顾名思义，围棋棋子都是黑白子互相包围在一起，属于线性不可分。但假设有一个武林高手暗运掌力，忽然快速往棋盘上一拍，让白子黑子都垂直往上飞起，同时让黑子飞高一点，白子则相对低一些，这样，平面无法线性区分的黑白子在进入立体空间，多了高度这个维度之后就体现出了区别。这时，只要往飞升的黑白子之间塞入一张薄纸，就把两种棋子分开了（见图8-2）。二维称“线”，三维称“面”，超过三维的就不另外改名字了，统一称“超平面”。
这个解释不但未说清楚，反而引入了两个很让人困扰的问题。一个理论层面的质疑——为什么映射到高维就能保证正负类能够上下分开？一个是应用层面的问题——这个高维空间要怎么找？变成高维空间容易，增加一个维度就能达到提升空间维度，一直增加下去也就成为高维空间，可是肯定不是简单地增加维度就能分开，还得给原有数据点在新的空间安排位置吧，那么怎么安排才合适呢？
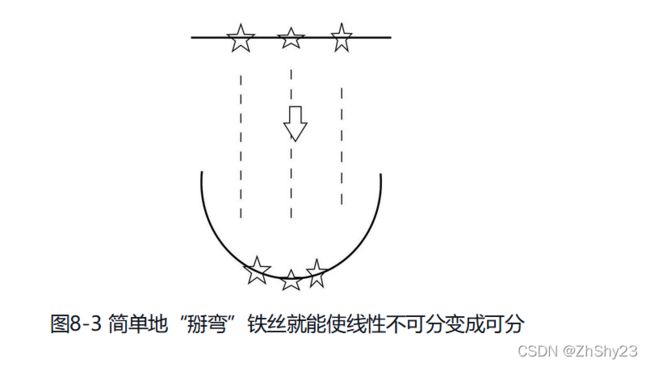
我们把问题形象化，为这个“你中有我，我中有你”想象一个具体的样子。不如就想象为一根铁丝，上面串了三枚五角星，我们的目标是用一条直线分出中间的五角星。显然这是一个线性不可分问题。无论直线怎么摆放，中间的五角星一定都会至少与一枚侧边的五角星在一起，从而无法正确区分。不过，对于这个看似不可能的任务，只要稍微弯一下铁丝，使铁丝形成一个U型，这时中间的五角星处在了低端，而两边的五角星被抬高，再往中间插入一条直线，就能正确区分二者了。见图8-3。
既然是线性不可分，那么可以推想需要区别的两类数据点处于一种“你中有我或者我中有你”的状态，最极端的就是一类数据被另一类“包围”，如果用红色和绿色区分这两类数据，图像就变成了“万绿丛中一点红”，在这种情况下显然不可能用任何一条直线来划分二者，也就是无法使用线性方法进行分类（如图8-4左图）。现在我们进行高维映射。高维映射其实是非常具体和实在的方法，没必要神秘化，这里我们选择肉眼可见的方法，即把高维映射想象成在二维空间中倒扣上一只肚子朝上的漏斗，二维空间就变成了三维空间，我们把漏斗移动到红色类（正方形）的数据上方，这时两种颜色的数据就出现了高度差，这时就可以通过插入一块平板分隔二者，也就是可以采用线性的方式进行非线性数据的区分了（如图8-4右图所示）。

总结一下，非线性数据之所以可以用线性方法区分，是因为给原本只有“左右”区别的五角星增加了“上下”维度，出现了线性可分的差别。从另一个角度看，这也是一种用映射方法来解决问题的案例。直线有直线方程，弧线有弧线方程，只需要通过一个映射，就能使得原本线性排列的数据呈弧线排列。对于机器学习用映射来解决问题我们并不陌生，回忆一下，Logistics回归里的“S型马甲”所用的就是这种手法。这就是增加维度来解决线性不可分问题的关键，知道当前分布是什么样子，也知道想要达到的分布是什么样子的，那么，就只要选择合适的映射函数了，也就解决了第二个问题。

二、支持向量机分类的算法原理

1. 基本思路

(1) 最大间隔

支持向量机说到底就是一种“线性分类器”，它以“间隔”作为损失的度量，目标通过不断调整多维的“直线”——超平面，使得间隔最大化。所谓“支持向量”，就是所有数据点中直接参与计算使得间隔最大化的几个数据点，这是支持向量机的得名由来，也是支持向量机的全部核心算法。

(2) 高维映射

其核心就是通过映射，把线性不可分的数据变成线性可分，具体来说就是增加维度，如把原本排成一条直线的正负样本点“掰弯”，或者给原本平铺在同一平面上互相包围的正负样本点添加一个“漏勺”，也就是加了一维高度值，使得非线性分布出现了线性可分的差异，从而最终达到分离正负类的目的，实现用线性分类器对非线性可分样本点进行分类的效果。

(3) 核函数

核函数不是一种函数，而是一类功能性函数，能够在支持向量机中完成高维映射这种功能的函数都称为核函数，也就是说，只要数学函数满足要求，就都可以被用作核函数。不过，无论哪种核函数，其最根本的目的就是完成高维映射，具体完成两项工作，一是增加空间的维度，二是完成对现有数据从原空间到高维空间的映射。
也就是说，核函数和高维映射虽然在讲解时拆分成两个概念，其实都是一个过程，二者可以看作因和果的关系。我们必须首先选定一款核函数，才能通过核函数将数据集进行映射，从而得到高维映射的结果。

(4) 支持向量机的真正运行机制

真正的支持向量机是由间隔最大化和高维映射两大部件组成。间隔最大化是目标，支持向量机的损失函数依靠间隔计算，能让间隔达到最大的就是支持向量机要“学习”的过程。
高维映射用于解决线性不可分问题，可以理解为对数据的“预处理”。对于那些你中有我、间不容发的非线性分布数据，首先通过核函数映射至高维，映射后的数据集呈线性分布，为使用线性方法分类创造了条件。

使用支持向量机进行分类经过三个步骤：

1. 选取一个合适的数学函数作为核函数。
2. 使用核函数进行高维映射，数据点在映射后由原本的线性不可分变为线性可分。
3. 间隔最大化，用间隔作为度量分类效果的损失函数，最终找到能够让间隔最大的超平面，分类也就最终完成了。

(5) 核技巧

在支持向量机中，涉及“核”的术语实际上有三个，分别是核函数、核方法（KernelMethod）和核技巧（Kernel Trick）。核方法和核技巧就是提出需求，核函数则是给出解答。换而言之，核函数是一石二鸟，实际上是完成了两项独立的任务。

• 任务一是完成核方法提出的要求，就是如何将低维非线性数据映射成高维数据，从而变成线性可分。
• 任务二是完成核技巧提出的要求，之所以称为“技巧”，是因为核技巧主要是提高核方法的计算效率。
  计算间隔涉及向量点积运算，如果先进行高维映射再进行向量点积运算，这会导致运算量激增，尤其是高维向量运算，由于参加运算的维度增加了，运算量也会显著增加。
  核技巧简化了这个过程：只需要输入原始向量就能通过核技巧计算直接得到正确的点积结果，而不用把两个向量分别完成高维映射，再进行点积运算，即将两项工作用数学技巧一次就完成。由于无论是目标函数还是决策函数都只涉及输入样本与样本之间的内积，这一运算特点使得我们在实际使用支持向量机算法进行学习时，不需要显式地完成高维映射操作，只需要事先定义核函数即可得到等价的结果，还避免了高维向量的运算，明显提高了运算效果。能够同时满足核方法和核技巧两项要求，才是核函数完整的工作内容。

2. 数学解析

(1) 点到超平面的距离

支持向量机以“间隔”作为损失函数，支持向量机的学习过程就是使得间隔最大化的过程，想了解支持向量机的运转机制，首先就得知道间隔怎么计算。而支持向量机对间隔的定义其实很简单，就是作为支持向量的点到超平面的距离的和，这里的距离就是最常见的几何距离。我们用wx+b来表示超平面，点到三维平面的距离有现成的公式可以套用：
$$d=\frac{|A{x}_0+B{y}_0+C{z}_0+D|}{\sqrt{A^2+B^2+C^2}}\text{\hspace{1em}(8-1)}$$

类似的，对于点到N维超平面的距离r，可以用以下公式计算：

$${\gamma }^{(i)}=\frac{(w^T{x}^{(i)}+b)}{\Vert w\Vert }\text{\hspace{1em}(8-2)}$$

其中被除数$w{x}^{(i)}+b$是超平面的表达式，除数$\Vert w\Vert$就是我们前面所讲的L2范式的简略写法。点到N维超平面的距离的公式计算很简单，形式上与点到三维平面的公式类似，其实当w是三维向量时，二者就是等价的。支持向量机就使用这条公式来计算点到超平面的距离。

(2) 间隔最大化

支持向量机使用y=1表示正类的分类结果，使用y=-1表示负类的分类结果，既然y=wx+b要么大于或等于1，要么小于或等于-1，间隔是由正负类最近的两个数据点，也就是支持向量决定，因此间隔距离也就可以表示为$\frac{2}{\Vert w\Vert }$（见图8-5）。

我们的目的就是间隔最大化。2是一个常数，所以最大化间隔距离可以表示如下：
$$max\frac{1}{\Vert w\Vert }s.t.,y_i(w^T{x}_i+b)\ge 1,i=1,\cdots ,n\text{\hspace{1em}(8-3)}$$
右边的s.t．表示suject to，意思是受到约束，我们把之前的条件写上，相当于“在……的条件下”，使得左边式子最大。分母越小，分数越大，所以左式也可以表示如下：
$$min\frac{1}{2}\Vert w{\Vert }^2\text{\hspace{1em}(8-4)}$$
这个式子看起来计算很简单，就是求极值，但要注意后面多了个约束条件，问题就稍微变复杂了。这里不具体展开，只需要记得可以用拉格朗日乘子法转化成如下拉格朗日函数：
$$L(w,b,a)=\frac{1}{2}\Vert w{\Vert }^2+\sum _{i=1}^m{\alpha }_i[1-y_i(w^T{x}_i+b)]\text{\hspace{1em}(8-5)}$$
其中α被称为“拉格朗日乘子”。上式分别对w和b求导，并令导数为0，右式可转化为下式：
$$\sum _{i=1}^m{\alpha }_i-\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j\text{\hspace{1em}(8-6)}$$
这时问题就变成了：
$$\underset{\alpha }{\max }\sum _{i=1}^m{\alpha }_i-\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j\text{\hspace{1em}(8-7)}$$
约束条件为：
$$\begin{array}{rl}& s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0\\ & {\alpha }_i\ge 0\end{array}\text{\hspace{1em}(8-8)}$$

这个式子通常用二次规划算法SMO（Sequential Minimal Optimization）算法求解。上面的式子转化包含大量复杂的数学概念和运算，这里只需要注意两点，一是支持向量机使用拉格朗日乘子法搭配SMO算法求得间隔最大，二是转化式的末尾为计算$x_i^T{x}_j$，也就是两个向量的内积。正因为间隔最大化可以转化为向量内积的运算，才使得高维映射可以通过核技巧进行优化。

(3) 核函数

高维映射实际上也是一种函数映射，在支持向量机中，通常采用符号φ来表示这个将数据映射到高维空间的函数，向量xi经过高维映射后就变成了φ(x)i，这时超平面的表达式也就相应变成了wTφ(xi)+b。
根据上述间隔最大化的拉格朗日函数，我们知道需要进行两个向量的内积运算，那么映射后的内积运算为φ(xi)Tφ(xj) 。映射后向量变成高维向量，运算量将明显增加，直接运算会导致效率明显下降。
不过，我们也已经观察到，在间隔最大化的运算中只使用了高维向量内积运算的结果，而没有单独使用高维向量，也就是说，如果能较为简单地求出高维向量的内积，同样可以满足求解间隔最大化的条件。我们可以假设存在函数K，能够满足以下条件：

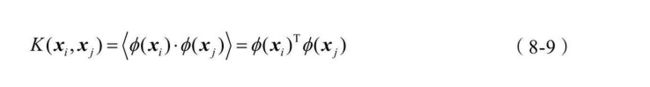
这里的函数K就是我们前面一再介绍的核函数。有了核函数，所有涉及φ(xi)Tφ(xj)的内积运算都可以通过K(xi,xj)简单求出，这也就是为什么核函数需要一边完成核方法的高维映射，一边又要完成核技巧的求内积结果。对于已知的映射函数φ，核函数是很容易计算的，但在大多数情况下，使用支持向量机时并不知道映射函数φ的具体形式，好在数学家已经证明，在这种情况下数学函数只需要满足几个条件，就同样可以作为核函数，也就确保了核函数的存在性。

3. 具体步骤

使用支持向量机算法，具体需要三步：

1. 选择核函数。
2. 核函数完成高维映射并完成计算间隔所需的内积运算，求得间隔。
3. 使用SMO等算法使得间隔最大。

三、在Python中使用支持向量机分类算法

在Scikit-Learn库中，支持向量机算法族都在sklearn.svm包中，当前版本一共有8个类。看起来也与其他机器学习算法族一样似乎有不少变种，其实并不太一样，支持向量机算法总的来说就一种，只是在核函数上有不同的选择，以及用于解决不同的问题，包括分类问题、回归问题和无监督学习问题中的异常点检测，具体为：

• LinearSVC类：基于线性核函数的支持向量机分类算法。
• LinearSVR类：基于线性核函数的支持向量机回归算法。
• SVC类：可选择多种核函数的支持向量机分类算法，通过“kernel”参数可以传入“linear”选择线性函数、传入“polynomial”选择多项式函数、传入“rbf”选择径向基函数、传入“sigmoid”选择Logistics函数作为核函数，以及设置“precomputed”使用预设核值矩阵。默认以径向基函数作为核函数。
• SVR类：可选择多种核函数的支持向量机回归算法。
• NuSVC类：与SVC类非常相似，但可通过参数“nu”设置支持向量的数量。
• NuSVR类：与SVR类非常相似，但可通过参数“nu”设置支持向量的数量。
• OneClassSVM类：用支持向量机算法解决无监督学习的异常点检测问题。

支持向量机分类算法可以通过SVC类调用使用，用法如下：

from sklearn.datasets import load_iris
from sklearn.svm import SVC
import warnings

warnings.filterwarnings("ignore")
X, y = load_iris(return_X_y=True)
clf = SVC().fit(X, y)
# 默认为径向基rbf，可通过kernel查看
print(clf.kernel)
print(clf.predict(X))
print(clf.score(X, y))
===============================================
rbf
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 2 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]
0.9866666666666667

四、支持向量机分类算法的使用场景

算法使用案例

国内安全软件厂商360推出的使用面很广的安全软件360杀毒和360安全卫士中都包含了一款名为“QVM人工智能引擎”的杀毒引擎，官方宣称QVM引擎无须频繁升级病毒库，就可以自主查杀各类变种木马病毒。QVM全名“Qihoo SupportVector Machine”，其实已明确表示用的就是支持向量机，推测原理为首先通过海量的病毒库训练支持向量机模型，然后再在用户本地对当前进程/文件是否有害进行分类判别。