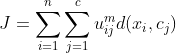mysql聚类函数排序_聚类算法大盘点 - 如鱼饮水，冷暖自知 - OSCHINA - 中文开源技术交流社区...

最近在关注聚类分析,了解了之后才发现,原来聚类分析里已经有这么丰富的成果,因此希望对其做个较全面的总结.

本文涉及到的聚类算法较多,请允许我慢慢更新.

1 层次聚类 (Agglomerative Clustering)

层次聚类也叫系统聚类,和K-means一起是最常用的聚类方式.

聚类效果如下:

 

它的实现方法有两种:

凝聚法

自下而上.从点作为个体簇开始.迭代时每一步合并两个最接近的簇,直到所有样本合并为一簇.

分裂法

自上而下.从包含所有样本点的某个簇开始.迭代时每一步分裂一个个体簇,直到所有簇都为个体簇.

1.1 凝聚层次聚类

凝聚法的关键是合并两个最接近的簇.合并的依据就是簇间的距离.不同的距离通常会得到不同的聚类结果.常用的有如下几种:

簇间最小距离

簇间最大距离

簇间平均距离

簇间质心距离

Ward方法

两个簇合的临近度定义为两个簇合并时导致的平方误离差平方和的增量.每次选取增量最小的两簇进行合并.该思想来源于方差分析:若分类正确,同类样平的离差平方和应该小,类与类之间的离差平方和应该大

我们可以看到,除Ward方法之外,簇间距离也依赖于不同簇中的点间距离.

点间距离可以采用欧氏距离,马氏距离,闵氏距离等等.

更多的点间距离可以看这篇文章 传送门

1.2 分裂层次聚类

分裂法与凝聚法刚好相反.每次分裂出一个个体簇.其判断标准有很多,例如”二分-kmeans”,”最小生成树聚类”等等.在这里先放着不讲.感兴趣的不妨转跳到对应位置看(目录有).

层次聚类的优缺点

优点:

1. 聚类质量较高.

缺点:

1. 算法复杂度

,空间复杂度

.这都相当昂贵.不利于其大规模运用. 

2. 缺乏全局目标函数.

2 基于原型的聚类 (Agglomerative Clustering)

基于原型的定义是每个对象到该簇的原型的距离比到其他簇的原型的距离更近。其中,原型指样本空间中具有代表性的点.

通俗地讲，就是对象离哪个簇近，这个对象就属于哪个簇。因此这种聚类的核心是如何确定簇的原型.

2.1 K-均值 (K-means)

取原型为样本均值.即样本质心.K-means中的K指簇的个数.

目标函数函数为:

 

其中,

 

是第j个中心质心;

是第i个样本 

可以认为,

是 

所属簇的特征函数; 也可认为是样本 

隶属于簇的隶属度.隶属为1,不隶属为0.

算法流程如下:

 

下图展示了对n个样本点进行K-Means聚类的效果，这里K取2。

K-means的优缺点

优点:

1. 计算速度快(算法复杂度

),原理简单. 

缺点:

1. K难以确定.

2. 受初始质心影响较大.

3. 对异常值非常敏感(平均确定质心).

2.2 二分K-均值 (bisecting K-means)

为克服 K-均值 算法收敛于局部最小值的问题,有人提出了另一个称为 二分K-均值 的算法.该算法首先将所有点作为一个簇,然后利用 K-means(K=2) 将该簇一分为二。之后选择其中一个簇继续进行划分,选择哪一个簇进行划分取决于对其划分是否可以最大程度降低总SSE的值。上述基于SSE的划分过程不断重复,直到得到用户指定的簇数目为止。

算法流程如下:

2.3 K-中心 (K-mediods)

从K-means中我们可以看到,它对异常点非常敏感.造成这个缺点的原因在于,每轮更新质点的时候是取簇中样本的平均.

要解决这个问题可以改变质点的更新方法.

K-mediods的核心思想

在 K-medoids中，我们将从当前簇中选取这样一个点作为中心点,使它到簇中其他所有点的距离之和最小。

其他步骤和K-means一致.

K-mediods的优缺点

优点:

1. 解决K-means对异常点敏感的问题

缺点:

1. 由于要对每个簇中样本点进行遍历来寻找中心点,因此计算复杂度

较K-means大.因此只适用于较小的样本.

2.4 模糊C均值 (FCM)

上面提到的K-均值聚类,其实它有另一个名字,C-均值聚类(HCM).要讲模糊C-均值,我们先从C-均值,也就是K-均值这个角度谈起.

HCM

从上面对K-均值算法的介绍中,我们已经知道了,K-均值的目标函数是:

 

其中,

 

这也是为什么叫H(Hard)CM.要么隶属该簇,要么不隶属该簇.太硬了.

引入模糊数学的观点,使得每个给定数据点用值在0，1间的隶度来确定其属于各个组的程度,便得到FCM的核心思想.

FCM

FCM的目标函数是

 

其中

介于0,1之间;也就是说,每个样本对各个簇都有一个隶属度,不再像HCM那样要么属于,要么不属于.更”模糊” 

)为控制算法模糊程度的参数. 

而且,对任意样本

满足: 

 

借助拉格朗日乘子,我们将限制条件整合到目标函数中得到新的目标函数

 

即在每一轮迭代中,要寻找

使得目标函数最小. 

下面我们对其进行求解:

当

为欧氏距离,

对中心

求偏导并令其为0,有 

 

对变量

求偏导并令其为0,有: 

 

 

为了使公式(4)满足条件

,我们将公式(4)代入条件,得到: 

 

 

 

看,我们得到了公式(5),即

所需满足的条件.接下来将公式(5)代回到公式(4),我们得到: 

 

 

 

数学推导到这里就结束了,我们关键再看一下公式(2)与公式(6).这两个公式分别决定了簇中心与隶属矩阵的更新.

 

模糊C均值的算法流程如下:

 

当算法收敛,就可以得到聚类中心和各个样本对于各簇的隶属度值,从而完成了模糊聚类划分.如果有需要,还可以将模糊聚类结果进行去模糊化.即用一定规则把模糊聚类划分为确定性分类.

3 基于密度的聚类

基于密度的聚类寻找被低密度区域分离的高密度区域.

对密度的不同定义衍生出不同的聚类方式

3.1 DBSCAN

DBSCAN,全称为 Density-Based Spatial Clustering of Applications with Noise.从名字可以看出,它能识别噪声.当然,噪声不属于任何一类.

DBSCAN用基于中心的方法定义密度.基于中心,指根据中心邻域内样点的数量衡量密度.

DBSCAN的预备知识.

核心点(core point): 给定邻域半径Eps(

),样本点个数MinPts.若该点的Eps邻域内包含的样本点数>MinPts,则认为该点为核心点.

边界点(border point): 该点不是核心点,但其在某个核心点的Eps邻域内.

噪声点(noise point): 该点既非核心点,也非边界点.

直接密度可达:若p在q的Eps邻域内,且q为核心点,则认为,p从q出发是直接密度可达的.

密度可达: 若存在某一样本链

.

从

出发是直接密度可达的,则认为

从

密度可达.

密度相连: 若p,q都是从某点O密度可达的,则认为p,q密度相连.

DBSCAN的核心思想:

寻找最大的密度相连集合,并标记其为同一类.Eps(邻域半径)与Minpts(最少点数)由经验确定.

 

图中A为核心点; B,C为边界点；N为噪声点;

B从A出发密度可达; C从A出发密度可达；A,B,C,红点密度相连.因此该图中{A,B,C,红点}为一簇

DBSCAN的算法流程

聚类效果:

DBSCAN算法优缺点:

优点:

1. 多次运行产生同样结果

2. 自动确定簇的个数,不需设置初始化质心

3. 可发现不同形状的簇

缺点:

1. 复杂度

,较K-means大.使用距离索引可降低复杂度到

. 

2. 当簇具有不同密度时,表现不佳(只能设置一组Eps和Minpts)

3. 与K-means相比,DBSCAN会合并重叠的簇;而K-means可以发现重叠的簇

3.2 OPTICS

讲DBSCAN时,我们说它有一个缺点:当簇具有不同密度时,表现不佳(只能设置一组Eps和Minpts).如下图所示:

 

图中显示了隐藏在噪声中的4个簇.簇和噪声的密度由明暗度表示.左方框内的噪声密度与簇C,簇D相等.这时候.若设置高密度为阈值,可以识别出簇A与簇B,但簇C与簇D会被认为是噪声.若设置低密度为阈值,可以识别出簇C与簇D,但左方框内所有样本点会被认为是同一簇(包括噪声)

为了解决DBSCAN这个弊端,有人提出了OPTICS(Ordering Points To Identify the CluStering)算法.

为了更细致地刻画样本密度情况,我们在DBSCAN的基础上多定义两个概念.

核心距离(core-distance):

 

即,给定MinPts,核心距离指使一个点成为核心点的最小邻域半径.

可达距离(reachability-distance):

 

即,从p直接密度可达o的最小邻域半径.(隐含前提是,p为核心点).显然,空间密度越大,p与相邻点的可达距离就越小

OPTICS算法的核心思想:

对样本点朝着尽量稠密的空间进行遍历,记录每次迭代中样本点的可达距离,得到可达图.

由于我们是沿着尽量稠密的方向进行遍历,因此可达距离在逼近密度中心之前必然是递减的;而远离密度中心时必然是递增的.因此,可根据可达图判断出密度中心(极小值点),从而进行簇的划分.

算法流程

聚类效果:

算法优缺点:

优点:

可识别具有不同密度的簇.

缺点:

算法复杂度为

3.3 DENCLUE

DENCLUE (DENsity CLUstering). 它用与每个点相关联的影响函数之和对点集的总密度建模.结果总密度函数将具有局部尖峰(即局部密度最大值),以这些局部尖峰进行定簇.

具体地说,每个尖峰为簇的中心.对于每个样本点,通过爬山过程,寻找其最近的尖峰,认为其与该尖峰相关联,并标记为对应簇.这与K-means有点类似.只不过K-means通过初始化随机中心并迭代得到最后的簇中心.而DENCLUE则根据核函数局部尖峰定义簇中心.

同时,可以对核密度峰值加一个阈值限制.小于阈值的局部尖峰与其相关联的样本点都将认为是噪声,可以丢弃.

下面用图来作直观解释.

 

如图所示,根据局部尖峰将这一维数据划分为A,B,C,D,E五簇(虚线为界)

加上阈值

后,簇C(虚线为界)认为是噪声点,可以舍弃. 

这里值得注意的是,与簇D相关联但小于阈值的样本点依然保留.类似于DBSCAN中的边界点.

由于簇D与簇E相连接的山谷依然大于阈值,因此可以将簇D与簇E合并为一簇;而簇A与簇B之间相连接的山谷小于阈值,因此簇A与簇B依然各自为一簇.

因此,添加阈值限制后可将数据集划分为三簇.

核密度估计(density estimation)

从上面的过程我们也可以看到,怎样估计核密度成为该算法的核心.

核密度估计这种技术的目标是通过函数描述数据的分布.对于核密度估计,每个点对总核密度的贡献用一个影响(influence)或核函数(kernel function)表示.总的核密度是与每个点相关联的影响函数之和.

通常,核函数是对称的,而且它的值随到点的距离增加而减少.例如,高斯核函数就是一个典型例子.

高斯核函数(对于某个点p):

 

其实就是高斯分布的核.其中x为网格中某一点.

该函数显示了样本点p对定义域中某点x的影响.

因此,x的总核密度为:

 

下图给出了高斯核总密度函数的计算例子

算法流程

算法优缺点

优点:

1. 核密度的引入给出了密度的一个精确定义.较DBSCAN更具理论依据

缺点:

1. 密度的精确定义带来了算法复杂度的增加.定义域网格中每个点都要遍历所有样本点以计算总核密度.网格大小确定了计算开销:网格大,计算量小,精度降低;网格小,计算量大,精度提高.

4 基于网格的聚类

基于网格的聚类,其基本思想是:

将每个属性的可能值分割成许多相邻的区间,创建网格单元的集合(类似于对各维特征进行等宽或等深分箱).将每个样本映射到网格单元中,同时统计每个网格单元的信息,如样本数,均值,中位数,最大最小值,分布等.之后所有处理的基本单位都是网格单元.

删除密度低于某个指定阈值

的网格单元.

由稠密的单元组形成簇

ps:可以看到,基于网格的聚类或多或少与密度有关系

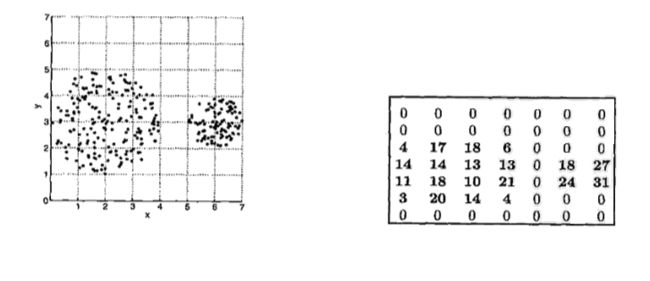
举个二维例子

 

若取阈值为8,则按单元格密度可划分为两类:

4.1 STING

STING (STatistical INformation Grid)算法本用于查询.但稍微修改一下便可用于聚类.

下面先介绍STING查询算法.

 

如图,我们将样本映射到不同分辨率的网格中.

其中,高层的每个单元被划分为多个低一层的单元,如下图:

STING查询算法流程

首先，在层次结构中选定一层作为查询处理的开始层。

对当前层次的每个单元，我们根据其统计信息，考察该单元与给定查询的关联程度。不相关的单元就不再考虑,低一层的处理就只检查剩余的相关单元。

这个处理过程反复进行，直到达到最底层。此时，如果查询要求被满足，那么返回相关单元的区域。否则，检索和进一步的处理落在相关单元中的数据，直到它们满足查询要求.

这样查询的优点是每层的查询都可以过滤大量不相关的样本,从而缩小查询范围.

STING聚类算法 将STING查询算法稍微修改一下就可以将其用于聚类.

其流程如下:

首先，在层次结构中选定一层作为聚类的开始层。

对当前层次的每个单元，我们根据其统计信息(如样本数,样本数百分比等)与设定的阈值，考察该单元是否为噪声单元.噪声单元内所有点认为是噪声点,不参与聚类.低一层的处理就只检查剩余的非噪声单元。

这个处理过程反复进行，直到达到最底层。最底层稠密的单元组形成簇.

STING聚类算法优缺点

优点:

1. 效率高.顺序扫描一次样本即可获得所有网格统计信息,时间复杂度

,n为样本数; 层次结构建立后,聚类时间是

,g为层数. 

缺点:

1. 非常依赖阈值选取.阈值太高,簇可能丢失; 阈值太低,本应分离的簇可能被合并,这也是基于网格的聚类通病.

2. 聚类的质量取决于网格结构的最底层的粒度.如果粒度比较细，处理的代价会显著增加；但是，如果网格结构最底层的粒度太粗，将会降低聚类分析的质量.

3. 聚类边界或者是水平的，或者是竖直的，没有斜的分界线.因此也不能识别圆形区域.这可能降低簇的质量和精确性.

4.2 CLIQUE

CLIQUE (CLustering In QUEst)是综合运用基于密度和网格方法优点所构造的聚类方法.其核心思想是利用先验原理,找出在高维数据空间中存在的低维簇.在讲该算法之前,我们先了解一下”子空间聚类”

子空间聚类

用特征的子集进行聚类.这可能会与特征全空间聚类的到的结果很不一样.有如下两个理由:

数据中关于少数属性的集合可能可以聚类,而关于其他的属性是随机分布的.

某些情况下,在不同的维集合中存在不同的簇.

举个例子:

 

全空间中,样本被分成了三个簇,分别用”菱形”,”正方形”,”三角形”.噪声用”圆形”标记.

这个图解释了两个事实:

圆点集在全空间中不形成簇,但在子空间中却可能成簇.

存在于高维空间中的簇在低维空间中也将成簇(其投影成簇).

但是我们会发现,要寻找所有子空间并寻找其中的簇,子空间的数量是指数级的.这显然不现实的.需要剪枝来去掉不必要的寻找.CLIQUE就是为了完成这个工作.

先验原理

从上面的第二个事实,我们可引出定理:如果一个网格单元在全特征空间中稠密,那在其子空间中也稠密.

我们称之为先验原理(与Apriori算法中的先验原理一致)

CLIQUE算法

利用先验原理,我们可以减小需要判断的子空间范围.

CLIQUE算法对子空间的簇的搜索,与Apriori算法中频繁项集的搜索一致.

先贴出算法流程:

用上面先验原理的图示来解释:

(一维子空间) a,b,c,d,e五维中 c,d,e三维根据网格密度判断,可以成簇,因此一维子空间候选集{c,d,e}

(二维子空间) 在一维子空间候选集的基础上进行元素组合,得到二维子空间集{cd,ce,de},判断集中每个子空间是否可以成簇.

例如,若cd空间中网格单元密度均小于阈值,则cd子空间不可以成簇.我们将cd剔除,后续不再考虑以其为子空间的高维空间;同理若判断{ce,de}成簇,则二维子空间候选集为{ce,de}

(三维子空间) 在二维子空间候选集的基础上增加一维(该维来自一维子空间候选集),得到三维子空间集{cde}.若cde成簇,则得到三维子空间候选集{cde};若不成簇,因为不存在三维稠密单元,算法结束.

如果还有不清楚的建议看一下Apriori算法.

算法优缺点

缺点:

1. 与所有基于网格的聚类算法一致,阈值与网格较难确定.

5 基于图的聚类

将数据集转化成图需要一个稀疏化的过程.

大家可以想,样本两两之间都会有一个邻近度.这个邻近度就是他们之间无向边的权重.这样就把数据集映射到一张完全图上.

但显然,这张图太复杂.完全图中看不出那些样本更相近.因此我们需要一个稀疏化的过程.

主要实现的方法两种:

把权重(邻近度)小于指定阈值的边去掉.

对每个样本点,仅保留k个最近邻的边.得到的称为K-最近邻图(k-nearest neighbor graph)

 

稀疏化后,我们在此图(稀疏邻近度图)基础上进行簇的划分.

5.1 最小生成树(MST)聚类

这个算法很简单直接:

根据图得到最小生成树(MST).

按邻近度从大到小依次断开一条边,得到一个新的簇.

直到所有样本都是一簇.

显然这是”分裂的层次聚类算法”的一种.

算法流程

5.2 OPOSSUM

OPOSSUM (Optimal Partitioning Of Sparse Similarities Using METIS) 从名字可以看出,这是一个”使用METIS算法对稀疏邻近度图进行最优划分” 的算法.

这里面有两个关键点:

METIS算法

最优划分

遗憾的是到现在为止我还没找到METIS算法的具体时间步骤.希望大家能补充.我自己也会留意查找资料,希望尽快完善.

算法流程

5.3 Chameleon

Chameleon算法的主要思想是:先对图进行划分,得到多个小簇,再利用自相似性概念对簇进行合并.

 

从上面的介绍可以看到,Chameleon算法的核心有两个

图的划分

自相似性的定义

图的划分. 从之前介绍的OPOSSUM算法我们可以看到,它对图的划分用的是METIS算法.因此在这里,对图的划分当然也可以用METIS算法.其他图的划分算法也是可以的.

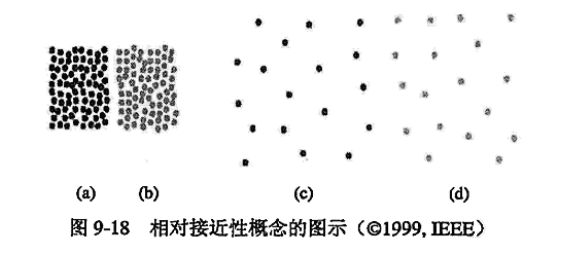
自相似性 (self-similarity)的定义 可以看到,算法后面对簇的合并有点类似凝聚的层次聚类算法.其实工作的过程也是一样的.我们回想凝聚的层次聚类算法,它用的相似度定义有:簇间最小距离,簇间质心距离等.

这可能会导致错误的合并.例如下图中,左方(a),(b)有少量间隔,右方(a),(b)几乎没有间隔.那么按照簇间最小距离的标准,应该合并右方的两簇.但显然,左方两簇更相似.

 

而且,包括k-means,DBSCAN等算法在内,都是全局静态的簇模型.静态指合并簇的标准都是不变的,事先指定的.这导致算法不能处理大小,形状,密度等簇特性在簇间变化很大的情况.如k-means假定了所有簇都是球形;DBSCAN则假定所有簇的密度都一致.

因此希望能够提出动态的簇模型,能解决上面提到的不足.

何谓”动态”?静态指全局都该满足某个特定参数标准;那么对应的,动态就是指不须全局满足,只要簇与簇之间满足该标准即可.

这也就是Chameleon算法合并簇的关键思想:仅当合并后的结果簇类似原来的两簇时,这两个簇才应当合并.(注意,不一定非要合并某两簇,这与凝聚层次聚类最后会合并到一簇有区别)

下面我们介绍一下”自相关性”(self-similarity).

1. 边割集

一个无向连通图，去掉一个边集可以使其变成两个连通分量(两分量间不连通).则这个边集就是边割集.权重和最小的边割集为最小边割集.

边割集的平均权重衡量了两分量的距离.平均权重越大,两分量相距越远.

边割集的权重之和衡量了两分量的联系程度.在平均权重差不多的情况下,边数越多,联系就越紧密.

“簇间边割集”指的是连接两簇的边(K-最近邻图中)的集合.

“簇内边割集”指的是二分该簇(分成两个大致相等分量)的边(K-最近邻图中)的集合.

2. 相对接近度 (Relative Closeness, RC)

相对接近度是”簇间边割集平均权重”与”簇内边割集平均权重”的比值,用于衡量”簇间距离”与”簇内距离”.

其数学定义为:

 

其中

指簇i,j间边割集的平均权重; 

指簇i内边割集的平均权重; 

指簇i的样本数; 

如下图:

 

右方两簇相对接近度比左方更大.因此右方更应当合并.

3. 相对互连度 (Relative Interconnectivity, RI)

相对互联度是”簇间边割集权和”与”簇内边割集权和”的比值,用于衡量了”簇间联系紧密程度”与”簇内联系紧密程度”.

其数学定义为:

 

其中

指簇i,j间边割集的权和; 

指簇i内边割集的最小权和; 

如下图:

 

上方两簇的相对互连度比下方两簇更大.因此上方两簇更应当合并.

4. 自相似性 (self-similarity)

RI与RC的不同组合方式产生了自相似性.一种方式是取最大化

.

为指定参数,一般大于1.即合并自相似度最大的两簇.当然若自相似度小于某个阈值,可以不合并.

算法流程:

算法优缺点

优点:

1. 动态簇模型,可很好地处理簇的大小,形状,密度不同的情况.

缺点:

1. 该算法以图的稀疏化与图的划分为基础.若该部分出问题,算法在后面步骤中是不能纠正的,只能合并.这在高维数据中是常常出现的.

6 基于神经网络的聚类

6.1 SOM

一种可用于聚类的神经网络模型.现在还没系统地学习神经网络,因此先挖个坑,日后再填.

The End

断断续续写了半个月,终于是将这篇关于聚类的总结写完了.写的过程中查找资料,发现里也有比较系统的论述,因此文中的图很多都来自.也加上了很多自己的理解和其他资料的补充.

各位读者如果发现哪里有批漏,请一定联系我(文章最下方有我的邮箱).能得到大家的指点是我的荣幸!

如有需要转载的也请告知我,并注明出处.