【数据压缩】DPCM编码实验

一.DPCM编码原理

在一个DPCM系统中，需要设计预测器和量化器两部分。

在本次实验中，我们采取左向预测和8bit均匀量化。

左向预测：

即将当前像素的左边像素作为预测，两像素值相减即为当前像素的预测误差值。

对于第一列像素，默认取其预测值均为128.

8bit均匀量化：

图像本身是8bit（灰度值为0-255），所以如果相减值就会变为-255——+255

为了进行8bit量化，要将预测误差值（即像素相减的差）/2+128，使其范围为0-255。（量化插值b=a/2）。之后需要进行反量化值c，将量化插值b乘2（c=b*2）。之后再将反量化值c与左侧像素预测值相加得到本像素预测值。

二.实验过程内容分析

1.本次实验需要三个文件

一个输入文件，一个预测误差图像文件，一个重建图像文件

    char* orifilename = NULL;
	char* prefilename = NULL;
	char* recfilename = NULL;

	orifilename = argv[1];
	prefilename = argv[2];
	recfilename = argv[3];

	FILE* fp1 = fopen(orifilename, "rb");
	FILE* fp2 = fopen(prefilename, "wb");
	FILE* fp3 = fopen(recfilename, "wb");

2.分配三个主要缓冲区

（1）oribuffer是原灰度图像的缓冲区

（2）prebuffer是预测误差图像的缓冲区

（3）recbuffer是重建图像的缓冲区

    for (int i = 0; i < height; i++)
	{
		for (int j = 0; j < width; j++)
		{
			if (j == 0)
			{
				*(recbuffer + i * width + j) = 128;
				*(prebuffer + i * width + j) = *(oribuffer + i * width + j) - 128;
			}
			else
			{
				p1 = *(oribuffer + i * width + j) - *(oribuffer + i * width + j - 1);//误差
				if (p1 % 2 == 0)
					p2 = p1 / 2 + 128;//8bit量化
				else
					p2 = (p1 - 1) / 2 + 128;//8bit量化
				*(prebuffer + i * width + j) = unsigned char(p2);
				p3 = unsigned char(p2 * 2);//反量化
				*(recbuffer + i * width + j) = *(oribuffer + i * width + j - 1) + p3;
			}
		}
	}

三.实验结果分析

原图像	预测误差图像	重建图像

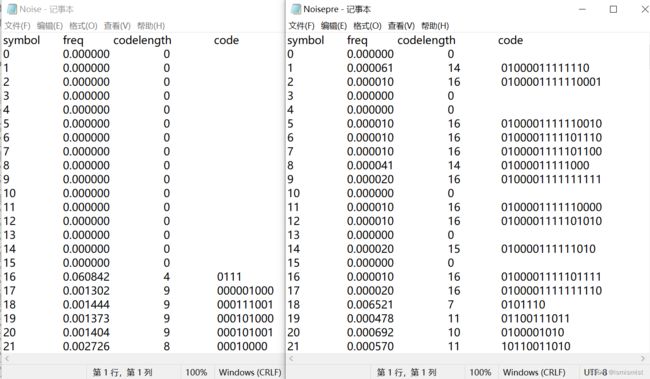
输出码流：

原图概率分布图	预测误差图像概率分布图

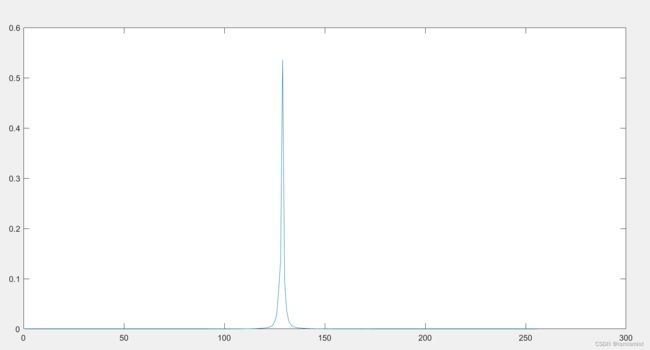压缩比：DPCM+熵编码：32.47%；仅进行熵编码：90.28%

压缩质量（PSNR）： 42.7887

原图像	预测误差图像	重建图像

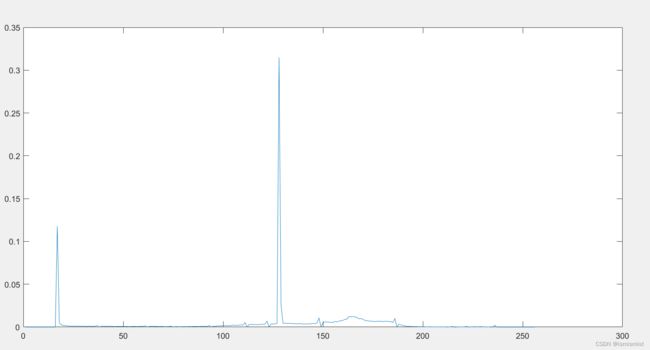
 输出码流：

原图像概率分布图	预测误差图像概率分布图

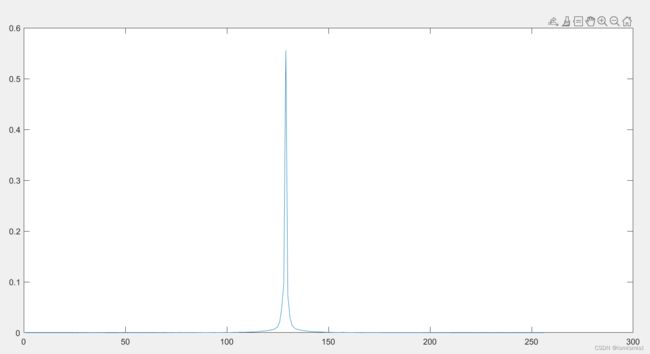压缩比：DPCM+熵编码：39.58%；仅进行熵编码：67.71%

压缩质量（PSNR）：42.595

原图像	预测误差图像	重建图像

 输出码流：

原图像概率分布图	预测误差图像概率分布图

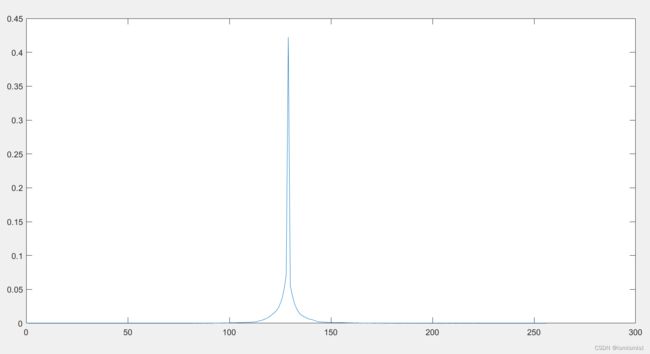压缩比：DPCM+熵编码：48.96%；仅进行熵编码：77.08%

压缩质量（PSNR）：34.9135

原图像	预测误差图像	重建图像

输出码流：

原图像概率分布图	预测误差图像概率分布图

压缩比：DPCM+熵编码：42.71%；仅进行熵编码：76.04%

压缩质量（PSNR）：34.894

原图像	预测误差图像	重建图像

输出码流：

原图像概率分布图	预测误差图像概率分布图

压缩比：DPCM+熵编码：46.88%；仅进行熵编码：71.88%

压缩质量（PSNR）：34.9002

原图像	预测误差图像	重建图像

输出码流：

原图像概率分布图	预测误差图像概率分布图

压缩比：DPCM+熵编码：75%；仅进行熵编码：70.83%

压缩质量（PSNR）：35.1973

原图像	预测误差图像	重建图像

输出码流：

原图像概率分布图	预测误差图像概率分布图

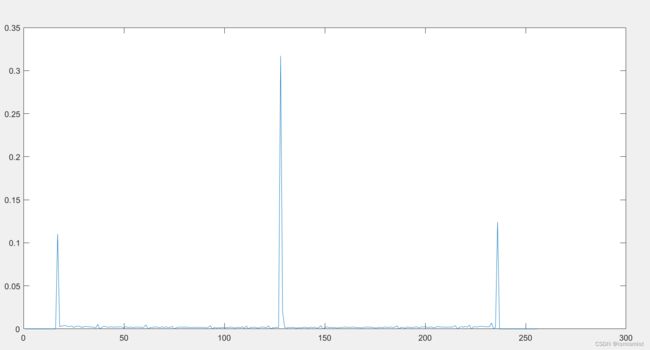压缩比：DPCM+熵编码：72.92%；仅进行熵编码：65.625%

压缩质量（PSNR）：33.5387

总结：

随机噪声（Noise）图像，像素间相关性不强，预测误差图中像素分布无规律，DPCM+熵编码压缩比反而不如直接熵编码的压缩比大。

zone图像，边缘变化很快，0-255交替出现，DPCM+熵编码的压缩比比直接熵编码的压缩比更大。

其它图像DPCM+熵编码的压缩比显然更好。

由PSNR的值可见（全部大于30），图片压缩质量很好。

四.完整代码

#include
#include
#include
using namespace std;

int main(int argc, char** argv)
{
	char* orifilename = NULL;
	char* prefilename = NULL;
	char* recfilename = NULL;

	orifilename = argv[1];
	prefilename = argv[2];
	recfilename = argv[3];

	FILE* fp1 = fopen(orifilename, "rb");
	FILE* fp2 = fopen(prefilename, "wb");
	FILE* fp3 = fopen(recfilename, "wb");

	if (fp1 == NULL)
		cout << "cannot find oriyuv" << endl;
	if (fp2 == NULL)
		cout << "cannot find preyuv" << endl;
	if (fp3 == NULL)
		cout << "cannot find recyubv" << endl;

	unsigned char* oribuffer;
	unsigned char* prebuffer;
	unsigned char* recbuffer;
	unsigned char* u_buffer;
	unsigned char* v_buffer;

	int width = atoi(argv[4]);
	int height = atoi(argv[5]);

	oribuffer = (unsigned char*)malloc(width * height * 1.5);
	prebuffer = (unsigned char*)malloc(width * height * 1.5);
	recbuffer = (unsigned char*)malloc(width * height);
	u_buffer = (unsigned char*)malloc(width * height * 1 / 4);
	v_buffer = (unsigned char*)malloc(width * height * 1 / 4);

	fread(oribuffer, sizeof(unsigned char), width * height, fp1);

	int p1;
	int p2;
	unsigned char p3;

	for (int i = 0; i < height; i++)
	{
		for (int j = 0; j < width; j++)
		{
			if (j == 0)
			{
				*(recbuffer + i * width + j) = 128;
				*(prebuffer + i * width + j) = *(oribuffer + i * width + j) - 128;
			}
			else
			{
				p1 = *(oribuffer + i * width + j) - *(oribuffer + i * width + j - 1);//误差
				if (p1 % 2 == 0)
					p2 = p1 / 2 + 128;//8bit量化
				else
					p2 = (p1 - 1) / 2 + 128;//8bit量化
				*(prebuffer + i * width + j) = unsigned char(p2);
				p3 = unsigned char(p2 * 2);//反量化
				*(recbuffer + i * width + j) = *(oribuffer + i * width + j - 1) + p3;
			}
		}
	}

	for (int i = 0; i < height / 2; i++)
	{
		for (int j = 0; j < width / 2; j++)
		{
			*(u_buffer + i * width / 2 + j) = 128;
			*(v_buffer + i * width / 2 + j) = 128;
		}
	}


	fwrite(recbuffer, 1, width * height, fp3);
	fwrite(u_buffer, 1, width * height / 4, fp3);
	fwrite(v_buffer, 1, width * height / 4, fp3);

	fwrite(prebuffer, 1, width * height, fp2);
	fwrite(u_buffer, 1, width * height / 4, fp2);
	fwrite(v_buffer, 1, width * height / 4, fp2);

	int max = 255;
	double mse = 0;
	for (int i = 0; i < width * height; i++)
	{
		mse += (double(oribuffer[i]) - double(recbuffer[i])) * (double(oribuffer[i]) - double(recbuffer[i]));  //分子
	}
	mse = (double)mse / (double)(width * height);
	double psnr = 10 * log10((double)(max * max) / mse);
	cout << "PSNR = " << psnr;

	return 0;
}