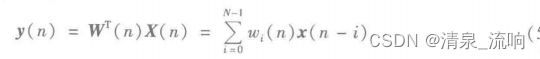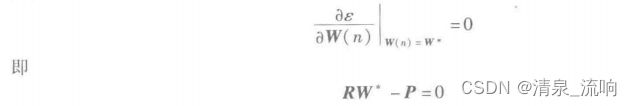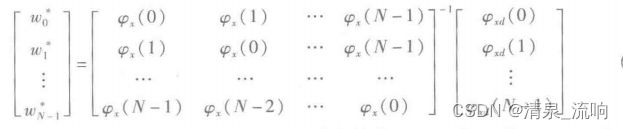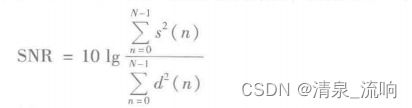传统语音增强——最小均方(LMS)自适应滤波算法
一、语音降噪的意义
语音降噪主要研究如何利用信号处理技术消除信号中的强噪声干扰,从而提高输出信噪比以提取出有用信号的技术。消除信号中噪声污染的通常方法是让受污染的信号通过一个能抑制噪声而让信号相对不变的滤波器,此滤波器从信号不可检测的噪声场中取得输入,将此输入加以滤波,抵消其中的原始噪声,从而达到提高信噪比的目的。
然而,由于干扰通常都是随机的,从带噪语音中提取完全纯净的语音几乎不可能。在这种情况下,语音增强的目的主要有两个:一是改进语音质量,消除背景噪声,使听者乐于接受,不感觉疲劳,这是一种主观度量;二是提高语音可懂度,这是一种客观度量。这两个目的往往不能兼得,所以实际应用中总是视具体情况而有所侧重的。
根据语音和噪声的特点,出现了很多种语音增强算法。比较常用的有谱减法、维纳滤波法、卡尔曼滤波法、自适应滤波法等。此外,随着科学技术的发展又出现了一些新的增强技术,如基于神经网络的语音增强、基于HMM的语音增强、基于听觉感知的语音增强、基于多分辨率分析的语音增强、基于语音产生模型的线性滤波法、基于小波变换的语音增强方法、梳状滤波法、自相关法、基于语音模型的语音增强方法等。
二、LMS自适应滤波器原理
在信号处理中,对一个受到加性噪声污染的信号通常采用自适应滤波器进行降噪。自适应滤波器具有自动调节自身参数的能力,故它的设计要求,或对信号和噪声的先验知识需求较少。
所谓自适应滤波器就是利用前一时刻已获得的滤波器参数等结果,自动地调节现时刻的滤波器参数,以适应信号和噪声未知的随机变化的统计特性,从而实现最优滤波。因此,无论在信噪比(Signal to Noise Ratio,SNR)方面还是在语音可懂度方面,自适应滤波器都能获得较大的提高。
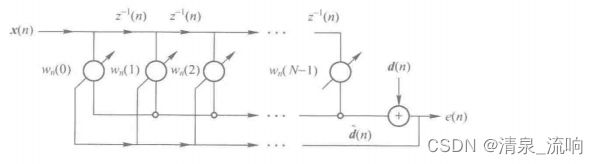
最小均方(LMS)自适应算法就是以已知期望响应和滤波器输出信号之间误差的方均值最小为准的,依据输入信号在迭代过程中估计梯度矢量,并更新权系数以达到最优的自适应迭代算法。LMS算法是一种梯度最速下降方法,其显著的优点是它的简单性,这种算法不需要计算相应的相关函数,也不需要进行矩阵运算。最简单的LMS滤波器结构下图所示,该结构最简单且易于实现而应用广泛。
滤波器的输出y(n)表示为
其中,X(n)为输入矢量,X(n)=[x(n),x(n-1),…,x(n-N+1)]^T,T为转置符,n为时间序列,W(n)为权系数矢量,W(n)=[w0(n),w1(n-1),…wN-1(n)]^T,N为滤波器阶数。
因此,对于LMS滤波结构,其误差为e(n)=d(n)-y(n)
方均误差ε表示为e=E[e^2(n)]=E[d(n)-y(n)]^2
代入y(n)到上式,有ε=E[d^2(n)]+W^T(n)RW(n)-2PW(n)
其中,R(n)=E[X(n)+X^T(n)]是NxN的自相关矩阵,它是输入信号采样值间的自相关矩阵;P=E[d(n)X^T(n)]为互相关矢量,代表理想信号d(n)与输入矢量X(n)的相关性。
在均方误差e达到最小时,得到最佳权系数W*=[w0*,w1*,…,wN-1*]T。它满足下列方程
如果矩阵R是满秩的,R^(-1)存在,可得到权系数的最佳值满足W*=R^(-1)P
其完整的矩阵表示式为
显然,φx(m)=E[x(n)x(n-m)]是x(n)的自相关值,φxd(R)=E[x(n)(n-k)]是x(n)与d(n)的互相关值。R和P的计算,要求出期望值E[·],在实际运算中不易实现。为此,对于一些在线或实时应用场合,多使用迭代算法,对每次采样值求出较佳权系数,称为采样值对采样值迭代算法。迭代算法可以避免复杂的R^(-1)和P的运算,又能实时求得近似解,因而切实可行。
LMS算法的基本设置
三、语音质量的性能指标
语音质量包括两方面内容:可懂度和自然度。前者对应语音的辨识水平。而后者则是衡量语音中字、单词和句的自然流畅程度。总体上看可以将语音质量评价分为两大类:主观评价和客观评价。
(1)主观评价
主观评价以人为主体来评价语音的质量。主观评价方法的优点是符合人类听话时对语音质量的感觉,目前得到了广泛的应用。常用的方法有平均意见得分(Mean Opinion Score,MOS)、诊断韵字测试(Diagnostic Rhyme Test,DRT)、诊断满意度测量(Diagnostic Acceptability Measure,DAM)等。语音质量的主观评价要求大量的人、大量次数的测听实验,以便能得到普遍接受的结果。但是由于主观评价耗费大、经历时间长,因此语音质量的主观评价不容易实现。
为了克服主观评价缺点,人们寻求一种能够方便、快捷地给出语音质量评价的客观评价方法。不过值得注意的是,研究语音客观评价的目的不是要用客观评价来完全替代主观评价,而是使客观评价成为一种既方便快捷又能够准确预测出主观评价价值的语音质量评价手段。尽管客观评价具有省时省力等优点,但它还不能反映人对语音质量的全部感觉,而且当前的大多客观评价方法都是以语音信号的时域、频域及变换域等特征参量作为评价依据,没有涉及语义、语法、语调等影响语音质量主观评价的重要因素。
(2)客观评价
语音质量客观评价方法采用某个特定的参数去表征语音通过增强或编码系统后的失真程度,并以此来评估处理系统的性能优劣。
1)信噪比(Signal-to-Noise Ratio,SNR)
SNR一直是衡量针对宽带噪声失真的语音增强计算的常规方法,其定义如下:
![]() 但要计算信噪比必须知道纯净语音信号,但在实际应用中这是不可能的。因此,SNR
但要计算信噪比必须知道纯净语音信号,但在实际应用中这是不可能的。因此,SNR
主要用于纯净语音信号和噪声信号都是已知的算法的仿真中。信噪比计算整个时间轴上的语
音信号与噪声信号的平均功率之比。由于语音信号是一种缓慢变化的短时平稳信号,因而在
不同时间段上的信噪比也应不一样。为了改善上面的问题,可以采用分段信噪比。
2) PESQ (Perceptual Evaluation of Speech Quality)
2001年2月,ITU-T推出了P.862标准《窄带电话网络端到端语音质量和话音编解码器质量的客观评价方法》,推荐使用语音质量感知评价(PESQ)算法,该建议是基于输入-输出方式的典型算法,效果良好。
PESQ算法需要带噪的衰减信号和一个原始的参考信号。开始时将两个待比较的语音信号经过电平调整、输入滤波器滤波、时间对准和补偿、听觉变换之后,分别提取两路信号的参数,综合其时频特性,得到PESQ分数,最终将这个分数映射到主观平均意见分(MOS)。PESQ得分范围在-0.5~4.5之间。得分越高表示语音质量越好。
四、LMS语音增强实验
信噪比计算函数SNR_Calc
名称:SNR_Calc
功能:计算信噪比。
调用格式:
snr=SNR_Calc(x,xn)
说明:输入信号x是输入的纯净语音信号;xn是输入的含噪信号。输出参数snr是计算的信噪比。
函数程序如下:
function snr=SNR_Calc(I,In)
% 计算带噪语音信号的信噪比
% I 是纯语音信号
% In 是带噪的语音信号
% 信噪比计算公式是
% snr=10*log10(Esignal/Enoise)
I=I(:)'; % 把数据转为一列
In=In(:)';
Ps=sum((I-mean(I)).^2); % 信号的能量
Pn=sum((I-In).^2); % 噪声的能量
snr=10*log10(Ps/Pn); % 信号的能量与噪声的能量之比,再求分贝值自适应滤波函数LMS
名称:LMS 函数程序如下: 案例、用LMS自适应算法给语音减噪 程序如下: 运行结果如下: 实验使用到的语音数据下载链接如下: https://mp.csdn.net/mp_download/manage/download/UpDetailed 参考文献:语音信号处理实验教程;梁瑞宇、赵力、魏昕(编著)
功能:自适应滤波器。
调用格式:
[yn,W,en] =LMS(xn,dn,M,mu,itr)
说明:输入参数xn是输入的含噪语音信号;dn是期望的语音信号;M是滤波器的阶数;mu是LMS滤波器步长;itr是迭代次数,默认为xn的长度(Mfunction [yn,W,en]=LMS(xn,dn,M,mu,itr)
% LMS(Least Mean Squre)算法
% 输入参数:
% xn 输入的信号序列 (列向量)
% dn 所期望的响应序列 (列向量)
% M 滤波器的阶数 (标量)
% mu 收敛因子(步长) (标量) 要求大于0,小于xn的相关矩阵最大特征值的倒数
% itr 迭代次数 (标量) 默认为xn的长度,Mclose all;clear all; clc;
[s, fs] = audioread('C5_1_y.wav'); % 读入数据文件
s=s-mean(s); % 消除直流分量
s=s/max(abs(s)); % 幅值归一
N=length(s); % 语音长度
time=(0:N-1)/fs; % 设置时间刻度
SNR=5; % 设置信噪比
r1=awgn(s,SNR,'measured','db');
M=64; % 设置M和mu
mu=0.001;
itr=length(r1);
snr1=SNR_Calc(s,r1); % 计算初始信噪比
[y,W,e]=LMS(r1,s,M,mu,itr);
output=e/max(abs(e)); % LMS滤波输出
snr2=SNR_Calc(s,output); % 计算滤波后的信噪比
snr=snr2-snr1;
SN1=snr1; SN2=snr2; SN3=snr;
fprintf('snr1=%5.4f snr2=%5.4f snr=%5.4f\n',snr1,snr2,snr);
% 作图
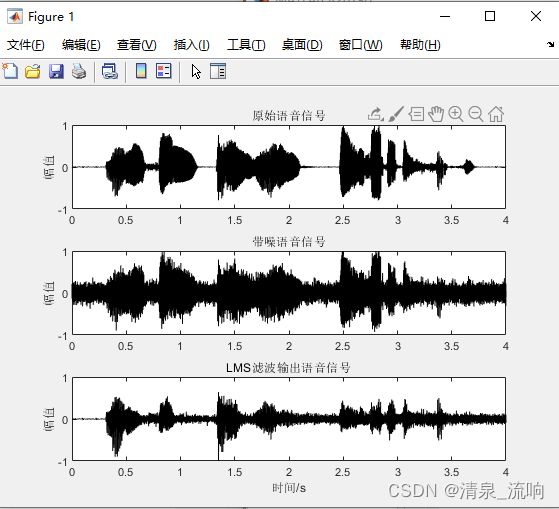
subplot 311; plot(time,s,'k'); ylabel('幅值')
ylim([-1 1 ]); title('原始语音信号');
subplot 312; plot(time,r1,'k'); ylabel('幅值')
ylim([-1 1 ]); title('带噪语音信号');
subplot 313; plot(time,output,'k');
ylim([-1 1 ]); title('LMS滤波输出语音信号');
xlabel('时间/s'); ylabel('幅值')