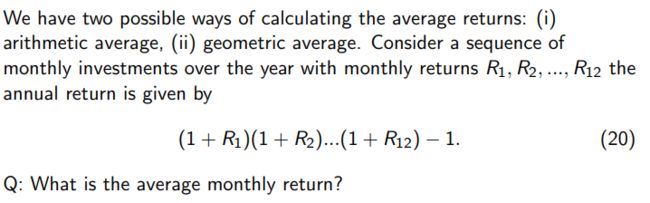【金融量化分析】#Financial Computation(利率、债券、期权相关数理知识与代码实现)
本篇文章涉及到的金融衍生品的计算,主要分为一下几个大类。flow chart
子:Bond债券相关计算
在此之前先回顾一下金融衍生品相关利率的知识。点这里上车
一:rates的计算
1:Effective return
two ways to calculate the average of return
1)arithmetic average
2) geometric average
Head:
Tom and Amy both bought a 20-year pension with different return schemes. Tom’s pension has first year interest rate of 3% and will increase by 0.5% every year whilst Amy’s pension has a continuous interest rate of 7%. Both pension pays the interest annually. Compare the benefits of the two pensions by computing their effective rates of return.
%% Solution:
InterestR_Tom=[3:0.5:12.5]/100;
EffectiveR_Tom=(prod(1+[3:0.5:12.5]/100))^(1/20)-1;% 用平均来算
EffectiveR_Tom=prod(
EffectiveR_AMY=exp(0.07)-1;
if EffectiveR_Tom>EffectiveR_AMY
disp('The pension of Tom has higher effective rate')
elseif EffectiveR_Tom<EffectiveR_AMY
disp('The pension of Amy has higher effective rate')
else
disp('The effective rates are equal')
end
二:Bondprice; Duration and convexity
编程思路:
首先wirte a user_defined matlab-code and call it 来计算Price,duration,convexity
then根据portifolio的性质进行编程
function [Price,duration,convexity] = DurationConvexity(Face,Coupon,Maturity,yield)
% BondPrice, Duration and Convexity
Time=0.5:0.5:Maturity; % time for payments
C = 0.5*Coupon*Face; % one coupon payment
Price = sum(C*exp(-yield*Time)) + Face*exp(-yield*Maturity);
duration= sum( (C* Time.* exp(-yield*Time) )/ Price )+Face*Maturity*exp(-yield*Maturity)/Price;
convexity = sum( (C.* (Time.^2).* exp(-yield*Time) )./ Price )+Face*(Maturity^2)*exp(-yield*Maturity)/Price;
end
Head:
Suppose you have two bonds in your portfolio, i.e. bond A and bond B, where both bonds have semi-annual coupon payments with annual coupon rates 4% and 5%, the maturities are 2 and 3 years, respectively. Both bonds have face value of 100 and the yields of these two bonds are given as 5% and 6.5%.
1、Calculate the value of your bond portfolio.
2、Calculate the duration of your bond portfolio.
3、Calculate the convexity of your bond portfolio.
4、Using the first order approximation and second order approximations calculate the relative change in the value of your bond portfolio if the yields go up with 25 basis points (25 basis points means 0.25%).
%% (a)
[price_A,duration_A,convexity_A] = DurationConvexity(100,0.04,2,0.05);
[price_B,duration_B,convexity_B] = DurationConvexity(100,0.05,3,0.065);
price_Portfolio=price_A+price_B
%% (b)
w_A=price_A/price_Portfolio;
w_B=price_B/price_Portfolio;
duration_Portfolio=w_A*duration_A+w_B*duration_B
%% calculate the weight of each asset multiply duration respectively
%% (c)
convexity_Portfolio=w_A*convexity_A+w_B*convexity_B
%% (d)
% first order approximation % 1st taylor expansion
PriceChange1=-0.0025*duration_Portfolio;
% second order approximation
PriceChange2=-0.0025*duration_Portfolio+0.5*(0.0025)^2*convexity_Portfolio;
#https://www.docin.com/p-35161143.html 一个问题
三:bootstrap 法 and related rates的计算
1:bootstrapping method
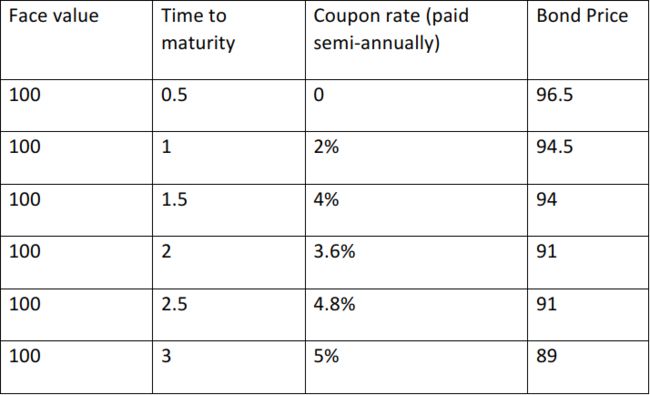
(a) Use Table 1 to calculate the zero rates using the bootstrapping method. Note that coupon rates are annual rates with semi-annual payments. For example, 2% per annum coupon rate means 1 dollar payment every six months for the face value of 100 dollars.
2:implied forward rates
(b) Calculate the implied forward rates using the zero rates obtained from 1 to 2 years and from 2 to 3 years time periods.
3:par yields
(c ) Calculate the par yields for the 1, 2, and 3 year maturities using the zero rates obtained.
4:duration and convexity
(d) Calculate the duration and convexity of the 3-year bond using the definition of duration and convexity.
5: approximation
(e) Suppose that the yields increase by 25 basis points (i.e. increase by 0.25%), then use the duration to approximate the change in the relative value of the 3-year bond. Second, use the duration and convexity to approximate the change in the relative value of the 3- year bond.
6:price change
(f) Now using your first order and second order approximations obtained in the previous part compare the approximations with the exact relative change in the value of the bond.
%% Solution A:
F=100
M=[0.5:0.5:3]
Cr=[0 2 4 3.6 4.8 5]/100
Coupon=Cr.*F/2;
BP=[96.5 94.5 94 91 91 89];
ZeroRate=[]
for i=1:length(Cr);
PaymentTime2=M(1:i); %t are the points of cash flows
ZeroRate(i)=(log(F+Coupon(i))-log(BP(i)-sum(Coupon(i)*exp(-ZeroRate(1:i-1).*PaymentTime2(1:end-1)))))/M(i);
end
Time_grid=[0.05:0.05:3];
R_spline=interp1(M,ZeroRate,Time_grid,'spline');
plot(M,ZeroRate,'o',Time_grid,R_spline,'r'),xlabel('Time'),ylabel('Zero rates'),title('Spline interpolation')
%% Solution B:
ForwardRate1=2*ZeroRate(4)-1*ZeroRate(2)
ForwardRate2=3*ZeroRate(6)-2*ZeroRate(4)
%% Solution C:
Discount1=exp(-1.*ZeroRate(2));
Discount2=exp(-2*ZeroRate(4));
Discount3=exp(-3*ZeroRate(6));
ParY1=(1-Discount1)/Discount1
ParY2=(1-Discount2)/sum([Discount1,Discount2])
ParY3=(1-Discount3)/sum([Discount1,Discount2,Discount3])
%% Solution (d)
[price_3,duration_3,convexity_3] = DurationConvexity(100,0.05,3,ZeroRate(6));
%% Solution (e)
% first order approximation
PriceChange1=-0.0025*duration_3
% second order approximation
PriceChange2=-0.0025*duration_3+0.5*(0.0025)^2*convexity_3
%% Solution (f)
[price_3b,duration_3b,convexity_3b] = DurationConvexity(100,0.05,3,(ZeroRate(6)+0.0025))
PriceChange3= (price_3b-price_3)/price_3b
四:The minimum variance portfolios
编程思路:首先编写一个计算出minvar的程序
在根据题目要求进行解答
function [w, minvar] = MinVarPortfolio(target, R, VCV)
% Tranpose R if R is a row vector
[row,col]=size(R);
if row<col
R=R';
end
L = length(R);
% Define and solve the linear system
A = [2.*VCV , R, ones(L,1) ; ...
R' , 0 , 0; ...
ones(1,L) , 0, 0];
b0 = [zeros(L,1); target; 1];
Sol= A \ b0; % analytical solution by gaussian elimination
w = Sol(1:end-2);
minvar= sqrt(w' * VCV * w);
end
Head:
Consider the following expected returns and covariance matrix given by
E=[0.05, 0.09, 0.10, 0.12]; % expected return
sigma=[0.09 0.1 -0.05 -0.03;0.10 0.16 0.02 0.04…
-0.05 0.02 0.25 0; -0.03 0.04 0 0.39]; %cov
Write the MATLAB script that will calculate the minimum variance portfolios for target returns within the range of 0.01 to 0.25 with increments of 0.005. Your goal is to obtain the expected returns and variances by solving the portfolio minimization with respect to each target return and combine them in a plot together with the expected return and volatility of the existing three stocks. This gives you the efficient frontier portfolios for given the set of three stocks. Finally, plot the efficient frontier using the appropriate MATLAB code.
R=[0.05, 0.09, 0.10, 0.12]; %expected return
VCV=[0.09 0.1 -0.05 -0.03; 0.10 0.16 0.02 0.04;...
-0.05 0.02 0.25 0; -0.03 0.04 0 0.39];% cov
TargetR=[0.01:0.005:0.25];
n=length(TargetR);
sigma=zeros(1,n);
for i=1:n
[w,sigma(i)]=MinVarPortfolio(TargetR(i),R,VCV);
end
plot(sigma,TargetR),xlabel('porfolio standard deviation'),ylabel('porfolio return'), title('efficient frontier')
丑:Option相关计算
一:Option中Implied Vol 计算
Impvol 是用市场已知的期权价格根据定价公式(option pricing 方法的不同)逆推得到的。
隐含波动率本身就是一个结果。
如果你想计算场外期权的价格,那用的那个参数就不叫隐含波动率。
一般认为,期权的隐含波动率代表市场交易者对未来标的资产波动率的预判给出的风险定价,也就是说,隐含波动率高代表未来标的资产的价格波动可能会比较大,标的资产的不确定性高;而隐含波动率低则表示市场对于标的资产的波动率预期较低,标的资产的不确定性低。
Head: Suppose you are given the market price of a European call option as 3.68 dollars and the current underlying stock price is 40 dollars, strike price is 41 dollars, risk free rate is 3%, and maturity is 0.75 years. Given these parameters use the Matlab’s “fzero(…)” function, the bisection method, and the Newton’s method to find the implied volatility of the option.
1:fzero;bisection method and Newton’s method
%% Solution
Call=3.68;
S=40;
K=41;
r=0.03;
T=0.75;
% using fzero
F = @(x) blsprice(S,K,r,T,x) - Call;
impvol1 = fzero(F,0.2)
% solving implied volatility using the bisection method
a = 0.01; b = 0.99; M=40; epsilon = 0.0001; delta = 0.0001;
u = blsprice(S,K,r,T,a) - Call; % F(a)
v = blsprice(S,K,r,T,b) - Call; % F(b)
e = b-a;
if ( sign(u) == sign(v) )
disp('Change the interval [a,b]')
else
for k=1:M
e = e/2;
c = a + e;
w = blsprice(S,K,r,T,c) - Call; % F(midpoint)
if (abs(e)< delta) || (abs(w)< epsilon)
break
end
if(sign(w) ~= sign(u) )
b = c;
v = w;
else
a = c;
u = w;
end
end
end
impvol2=c
%using Newton's method to find the implied volatility of the option
x0=0.4;
M=10;
delta = 0.0001;
epsilon = 0.0001;
v = blsprice(S,K,r,T,x0) -Call;
flag = 0;
for i=1:M
x1 = x0 - v/ blsvega(S,K,r,T,x0);
v = blsprice(S,K,r,T,x1) - Call;
if (abs(x1-x0)<delta) || (abs(v)<epsilon)
flag =1;
break
end
x0 = x1;
end
impvol3=x1
对1:bisection的补充
The current stock price is 132 RMB. The risk-free rate is 3.5%. Use the bisection method to plot the implied volatility surface given the European call option prices with different strike level K and expiration time T
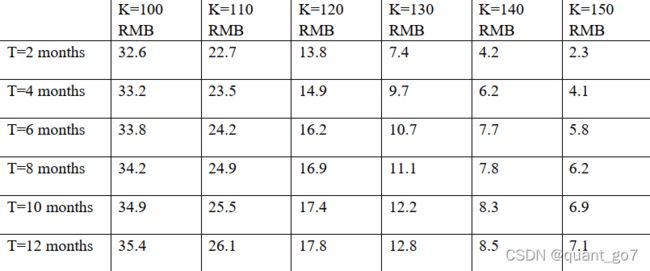
call the ImpliedVol function before
function IVol = ImpliedVol(Price,S,K,r,T)
% bisection method -- solving non-linear equations
a = -0.01;
b = 0.99;
M = 40;
delta = 0.0001;
epsilon = 0.0001;
u = blsprice(S,K,r,T,a) - Price; % F(a)
v = blsprice(S,K,r,T,b) - Price;
e = b-a;
if ( sign(u) == sign(v) )
disp('Change the interval [a,b]')
else
for k=1:M
e = e/2;
c = a + e;
w = blsprice(S,K,r,T,c) - Price;
if (abs(e)< delta) || (abs(w)< epsilon)
break
end
if(sign(w) ~= sign(u) )
b = c;
v = w;
else
a = c;
u = w;
end
end
end
IVol =c;
end
clear all;
S0=132;r=0.035;strikes=[100:10:150];time=[1/6:1/6:1];
Op=[32.6 22.7 13.8 7.4 4.2 2.3;...
33.2 23.5 14.9 9.7 6.2 4.1;...
33.8 24.2 16.2 10.7 7.7 5.8;...
34.2 24.9 16.9 11.1 7.8 6.2;...
34.9 25.5 17.4 12.2 8.3 6.9;...
35.4 26.1 17.8 12.8 8.5 7.1];
[t k]=size(Op);
impvol = zeros(t,k);
for i=1:t
for j=1:k
T=time(i);
K=strikes(j);
impvol(i,j) = ImpliedVol(Op(i,j),S0,K,r,T);% bisection method ,the"c" needs to change to -0.01 to narrow for the satisfied expression
end
end
figure
[X,Y]=meshgrid(time,strikes);
surf(X,Y,impvol);
figure
T_grid=[1/6:1/600:1];
S_grid=[100:0.1:150];
[X_grid Y_grid]=meshgrid(T_grid,S_grid);
impvolP=interp2(time,strikes,impvol,X_grid,Y_grid,'Spline');
surf(X_grid,Y_grid,impvolP);
二:Option valuation期权的定价
1:蒙卡模拟思想
蒙特卡洛数值思想为option定价的思路:

首先,根据股价服从Geometric BM, 对到期日S进行大量的采样,
then 得到大量的S_T ,计算max(S_T-K,0), 得到一组期权的payoffs。
最后,求出payoffs的均值,并折现,得到call option 的价值。
蒙卡定价的代码实现:
Head: Write a Matlab programme to verify put-call parity using the Monte Carlo Simulation.
%% Solution
function [call put parity] = MCPutCallParity(S0,K,r,sigma,T,M,N)
% M is the number of time step and N is the number of paths
% M主要是模拟大量的dt对应的epsilon,相当于迭代M次得到一个S_T,; N模拟不同的路径,得到N个S_T;.
dt = T/M;
call=0;
put=0;
for j=1:N % one stock price paths is generated in each iteration
Price(1) = S0;
for i=1:M
Price(i+1) = Price(i) * exp((r -sigma^2/2)*dt + sigma*sqrt(dt)*normrnd(0,1));
end
call = call + exp(-r*T)*max(Price(end) - K,0)/N;
put = put + exp(-r*T)*max(K - Price(end),0)/N;
end
right=call+K*exp(-r*T) %看跌-看涨平价关系式
left=put+S0;
parity=(abs(left-right)<1);
对1:(蒙特卡洛的补充)
Head: Assume that the stock price follows the following Geometric Brownian Motion with risk free rate 3.7%, volatility 32%, and current stock price 42USD. Implement the Monte Carlo simulation to find the price of an 1-year exotic option with the payoff function.
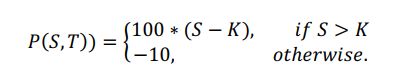
Where 0 is the current stock price, is the risk-free rate, and is the time to expiry. The strike level K is the norm of all daily stock prices before the expiry over T:
= ( ∈[1,])/
%% Solution
d = 250;
S0 = 42; r = 0.037; sigma=0.32; T = d/250;
dt = 1/250;
N = 1000;
E=0
for i=1:N
S(1) = S0;
for j=1:d
S(j+1) = S(j)* exp( (r-sigma^2/2)* dt + sigma*sqrt(dt)*normrnd(0,1) );
end
K = norm(S,2)/250;
if S(end)>K
E = E + 100*(S(end)-K)/N;
else
E = E -10/N;
end
end
2:BS公式进行定价
利用BS公式进行期权定价,需要注意call and put 对应的期权计算规则有差异。
另外思考一个问题
具体的公式可以看这篇blog☞
function Call = blsprice(S,K,r,T,sigma)
% BS formula for European call pricing
d1 = (1./(sigma.*sqrt(T))).*( log(S/K) + (r+sigma.^2/2).*T);
d2 = d1 - sigma.*sqrt(T);
Z1 = normcdf(d1,0,1);
Z2 = normcdf(d2,0,1);
Call = Z1*S - Z2*K*exp(-r*T);
end
function Put = blsprice(S,K,r,T,sigma)
% BS formula for European put pricing
d1 = (1./(sigma.*sqrt(T))).*( log(S/K) + (r+sigma.^2/2).*T);
d2 = d1 - sigma.*sqrt(T);
Z1 = normcdf(d1,0,1);
Z2 = normcdf(d2,0,1);
Put = (1-Z2)*K*exp(-r*T)-(1-Z1)*S;
end
对2:BS公式进行定价的补充
Head: Write a user-defined function EuropeanCallPrice(S0, r, sigma, T, K) to compute the European call option prices, where inputs r and sigma are vectors.
%% Solution
function call = EuropeanCallPrice(S,r,sigma,T,K)
if length(r)>1 & length(sigma>1)
[r1 c1]=size(r);
[r2 c2]=size(sigma);
if r1==r2|c1==c2
r=r';
end
end
d1 = (1./(sigma.*sqrt(T))).*( log(S/K) + (r+sigma.^2/2).*T);
d2 = d1 - sigma.*sqrt(T);
Z1 = normcdf(d1,0,1);
Z2 = normcdf(d2,0,1);
call = Z1*S - Z2*K.*exp(-r*T);
end
3:二叉树期权定价法 (二叉树需要Monte Carlo的思想)
课堂上还提到一种JRtree,可以思考一下。
具体的算法实现可以参考stochastic 计算中的第一题,上车
编程思路:
Step1 : 计算步长∆t=t/step ,计算上涨概率 u= e^σ∆t , 计算下跌概率 u= e^(-σ∆t)。
Step2 : 计算风险中性概率 p=(e^(-r∆t)-d)/(u-d),如果标的是期货,则风险中性概率修改为p=(1-d)/(u-d) 。
Step3 : 从左至右形成标的价格树,节点0的价格为S, 则假设至当前步v,标的价格共上升i 步,下降j步, 则步v标的价格 S_(i,j)=S_0uidj , 其中 i+j=v 。
Step4: 从右至左形成期权价格树,从最后一步的价格开始,同一步相邻节点(例如S_(i,j+1)和S_(i+1,j))的价格可推导出两相邻节点父节点S_(i,j)期权贴现价格为 〖DV〗(i,j)=(C(i,j+1)(1-p)+C_(i+1,j)*p)e^(-r∆t) ,最外层的贴现价值为零。 该节点看涨的行权价值为 E_(i,j)=max(S_(i,j+1)-K,0) ,看跌期权的行权价值为E_(i,j)=max(〖K-S〗(i,j+1),0) , 该节点的期权价值为 C(i,j) =max(〖DV〗(i,j), E(i,j) ) 。当步骤进行到根节点时,即为期权价格。
Head: Calculate the price of a European call option with initial stock price S0=100, K=97, r=0.03, T=0.75, σ =0.35, M=30 using the CRR binomial tree. Re-calculate the European call option price with M = 100 steps and compare with the Black-Scholes price, check the difference between two binomial tree prices.
S0=16;r=0.05;T=1;K=20;sigma=0.3;M=200;
[ call, put ] = BinomialEur_CRR( S0,K,r,T,sigma,M )
%% Solution
%BinomilEur_CRR.m
function [ call, put ] = BinomialEur_CRR( S0,K,r,T,sigma,M )
deltat = T/M;
discount = exp(-r*deltat);
A = 0.5*(exp(-r*deltat) + exp(r*deltat + sigma*sigma*deltat) );
u = A + sqrt(A*A - 1);
% u = exp(sigma.*sqrt(deltat)); %或者直接这样
d = 1/u;
p = (exp(r*deltat)-d)/(u-d); % risk neutral probability 风险定价原理
lattice = zeros(M+1,M+1);
for i=0:M
lattice(i+1,M+1)=max(0,S0*(u^i)*(d^(M-i))-K);% 历遍最后的股票价值(期权价值)
end
for j=M-1:-1:0
for i=0:j
lattice(i+1,j+1) = discount*...
(p*lattice(i+2,j+2) + (1-p)*lattice(i+1,j+2));
end
end
call = lattice(1,1);
put = call - S0 + K*exp(-r*T); %无套利原理
end
4:(CrankNicholson method 有限差分法)
想要了解 ?FDM 的背后原理?先看这个
Head: Given the Black-Scholes write the MATLAB code to solve the CrankNicholson method and price the European put option with the following parameters S0 = 100 (initial stock price), K = 101 (strike price), σ = 0.28 (volatility of the stock), rf = 0.03 (risk free rate), T = 0.75 (maturity). You can set ∆t = 0.01 and ∆S = 1.
CrankNicolson 其实是有限差分法的一种,来为期权定价。
编程思路:
首先设置一个远大于K的Smax,
function price = EuropeanCallCrankNicolson(S0, K, r, T, sigma, Smax, dS, dt)
% set up the grid and adjust the increments if necessary
M = round(Smax/dS);
dS = Smax/M;
N = round(T/dt);
dt = T/N;
Value = zeros(M+1,N+1);
vecS = linspace(0,Smax,M+1)';
vecI = 0:M;%股票价格
vecJ = 0:N;%时间
% set up boundary conditions:put
% Value(:,N+1) = max(K-VecS,0); % terminal condition , consider other payoffs
% Value(1,:) = K*exp(-r*dt*(N-VecJ)); % boundary condition
% Value(M+1,:) = 0; % boundary condition
% set up the terminal condition:call
Value(:,N+1) = max(vecS-K,0);
% set up the boundary conditions
Value(1,:) = 0;
Value(M+1,:) = Smax*exp(-r*dt*(N-vecJ));
% set up tridiagonal coeffients matrix 根据PDF的近似表达
alpha = 0.25*dt*(sigma^2*(vecI.^2) - r*vecI );
beta = -dt*0.5*(sigma^2*(vecI.^2) + r);
gamma= 0.25*dt*(sigma^2*(vecI.^2) + r*vecI);
M1 = -diag(alpha(3:M),-1) + diag(1-beta(2:M)) - diag(gamma(2:M-1),1);
[L,U] = lu(M1);
M2 = diag(alpha(3:M),-1) + diag(1+beta(2:M)) + diag(gamma(2:M-1),1);
% solve the sequence of linear systems
aux = zeros(M-1,1);
for j=N:-1:1
aux(1) = alpha(2) * (Value(1,j+1) + Value(1,j)) ; % other term from the boundary condition is zero
Value(2:M,j) = U \ ( L \ (M2*Value(2:M,j+1) + aux) );
end
impliedFDMprice = interp1(vecS, Value(:,1),S0);
end
5:美式期权 LSM(最小二乘蒙特卡洛)
https://blog.csdn.net/xiaowu1997/article/details/121921841
三:期权价格作图
Use a 200-step CRR binomial tree to compute the European call option prices given that:
0 = 16;
= [0: 0.0001: 0.05];
= 1;
= 20;
= [0: 0.01: 0.3].
Plot the option price surface with regards to the risk-free rate and the volatility.
clear all
S0=16;r=[0:0.0001:0.05];T=1;K=20;sigma=[0:0.01:0.3];M=200;
deltat = T/M;
call = zeros(length(r),length(sigma));
for k=1:length(r)
discount = exp(-r(k)*deltat);
for l=1:length(sigma)
A = 0.5*(exp(-r(k)*deltat) + exp(r(k)*deltat + sigma(l)*sigma(l)*deltat) );
u = A + sqrt(A*A - 1);
d = 1/u;
p = (exp(r(k)*deltat)-d)/(u-d);
lattice = zeros(M+1,M+1);
for i=0:M
lattice(i+1,M+1)=max(0,S0*(u^i)*(d^(M-i))-K);
end
for j=M-1:-1:0
for i=0:j
lattice(i+1,j+1) = discount*...
(p*lattice(i+2,j+2) + (1-p)*lattice(i+1,j+2));
end
end
call(k,l) = lattice(1,1);
end
end
figure
[X,Y]=meshgrid(sigma,r);
surf(X,Y,call);