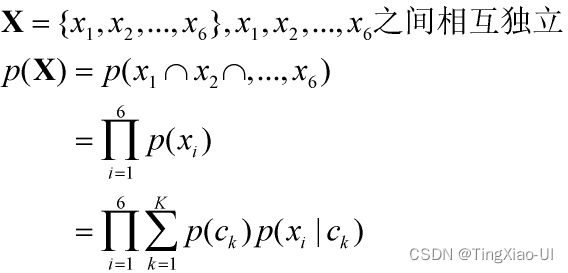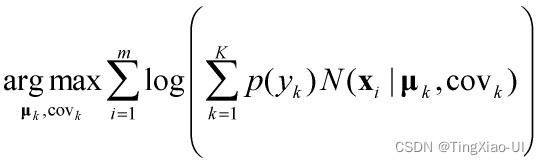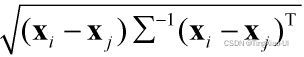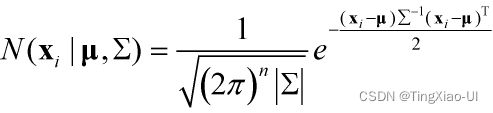机器学习中的高斯分布

• 高斯分布与数据预处理：数据分布转换
• 高斯分布与聚类：GMM
• 高斯分布与异常检测
• 高斯分布与马氏距离

高斯分布与数据预处理：数据分布转换

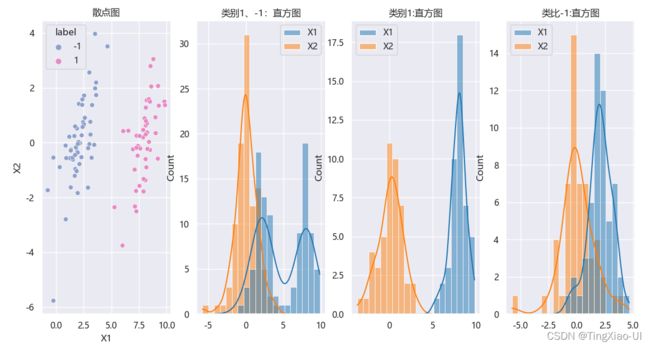
        当我们上手一个数据集时，往往第一件事就是了解每个特征是如何分布的。特征分布指的就是某个特征在整个数据集上的分布情况。如下图所示，为数据集的散点图、数据集的特征X1和特征X2的分布情况以及类别1和类别-1的特征分布情况

 代码如下

import pandas as pd
import matplotlib.pylot as plt
import seaborn as sea

def draw(inX):
    #筛选数据
    data1 = inX[inX['label']>0].iloc[:,:-1]
    data2 = inX[inX['label']<0].iloc[:,:-1]
    #设置主题
    sea.set_theme(style="darkgrid",palette=sea.color_palette("tab10"))
    fig, ax_arr = plt.subplots(1, 4, figsize=(10, 5))
    #显示分布情况
    #样本分布情况
    sea.scatterplot(data=inX, x='X1', y='X2', hue="label",ax=ax_arr[0], palette=sea.color_palette("Set2", 10)[2:4], sizes=(10, 200))
    ax_arr[0].set_title('散点图')
    #特征分布情况 
    sea.histplot(data=inX.iloc[:,:-1],bins=20,kde=True, ax=ax_arr[1])
    sea.histplot(data=data1, bins=20,kde=True, ax=ax_arr[2])
    sea.histplot(data=data2,bins=20,kde=True, ax=ax_arr[3])
    #标题
    ax_arr[1].set_title('类别1、-1：直方图')
    ax_arr[2].set_title('类别1:直方图')
    ax_arr[3].set_title('类比-1:直方图')

    plt.show()

if __name__=='__main__':
    # ******加载数据集**********
    trainData = 'testSet.txt'  # testSet.txt/secom.data/ex00.txt,ex0~9.txt
    baseData = pd.read_csv('./Data/'+trainData,sep='\t',names=['X1','X2','label'])
    #可视化数据
    draw(baseData)

为什么机器学习中很多分布都采用高斯分布？

        机器学习中许多模型都是基于数据服从高斯分布(不是严格服从高斯分布，近似也可以)的假设，很多以概率分布为核心的机器学习模型大部分也假设数据是高斯分布，比如生成模型：朴素贝叶斯分类、GMM。在高斯分布的情况下，我们使用相应的模型得到的结果才是稳健的。如果数据特征不是高斯分布，有时需要找到一个数学变换来把特征按照高斯分布进行变换。

        根据概率论中的中心极限定理，当样本容量无穷大时，许多分布的极限就是高斯分布(正态分布)，现实中的很多随机变量是由大量相互独立的随机因素的综合影响所形成的，而其中每一个因素在总的影响中所起的作用都是微小的，这种随机变量往往近似服从高斯分布（中心极限定理的客观背景）。

        从熵的角度来看，在已知数据的均值和方差的情况下(原数据分布类型未知)，高斯分布的熵是所有其他分布中最大的。按照熵标准，“最大熵”约等价于“同约束下最接近均匀分布”，即更符合实际。可以这样理解，“熵最大”是为了使理想更接近实际，让特殊逼近一般，从而使模型更具一般性。注意高斯分布的熵其实是由方差决定的，“高斯变量最大熵”是在方差固定的背景下的结论。不同的方差显然会带来不同的高斯分布，而熵越大的高斯分布方差越大——在实轴上也越接近“均匀”

熵：用来度量信息混乱程度

哪些模型假设数据服从高斯分布：

1. 涉及极大似然、EM的模型：逻辑回归、GMM、朴素贝叶斯......
2. 涉及计算方差最大的模型(最大熵分布)：PCA、LDA......
3. 一些文章说线性回归需要数据服从高斯分布，这种说法并不准确，应该是人们希望线性回归的残差分布服从高斯分布，若残差不符合高斯分布，说明模型性能差

如何检验特征是否服从高斯分布

        我们可以可视化数据来观察特征的分布情况，但是仅靠肉眼并不能确定特征的具体分布类型。可以使用Q-Q图(分位数图)来进行检验。

        用Q-Q图进行检验特征分布，简单讲就是把两个分布(待检验分布和已知分布)的分位数放在一起作比较，来检验待检验数据的特征分布情况。若两个分布(待检验分布和已知分布)相似，

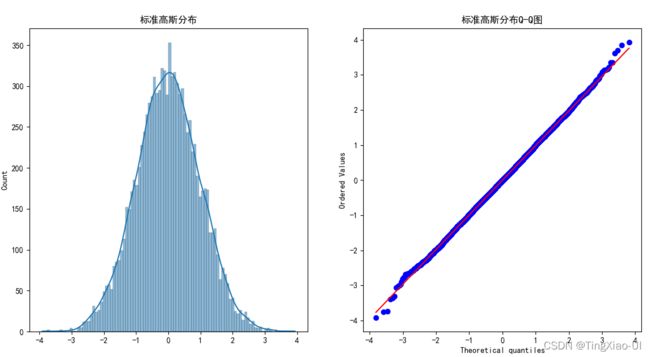
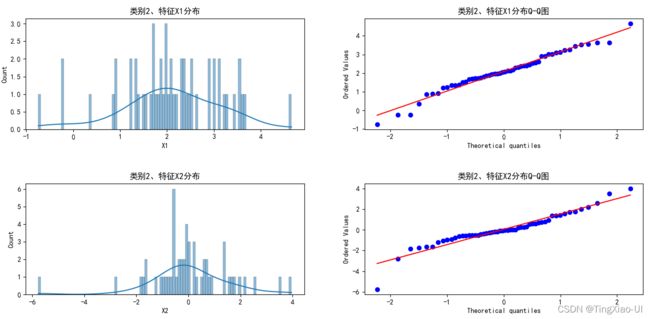
标准高斯分布图及其Q-Q图如下图所示

直方图表示连续型变量的频数分布，Q-Q图(分位数图)反映了待检验特征的实际分布与理论分布的符合程度，若特征服从高斯分布，则数据点与理论直线(图中红线)基本重合。

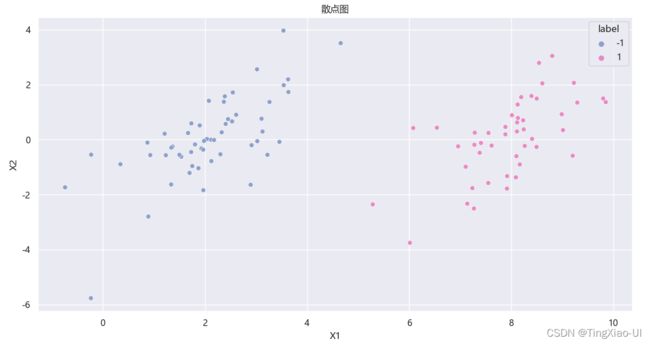
现有数据集样本散点图如下所示，具有两种类别

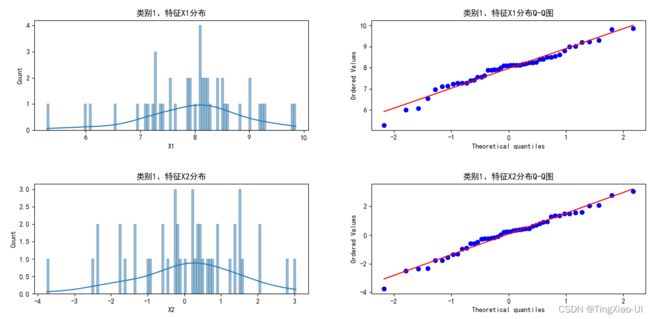
 分别绘制每个类别的每个特征的分布图

类别1：

 类别2：

 如上图所示，通过Q-Q图可以直观观察特征分布是否遵循高斯分布。

 偏度和峰度

        偏度（Skewness）可以反映倾斜的程度和方向（偏离水平对称），峰度（Kurtosis）可以反映相对于标准钟形曲线的中心峰的高度和尖锐程度。        

上述的特征分布检验方法比较主观，也可以通过非参数检验方法检验特征是否遵循高斯分布，如非参数检验：S-W检验、K-S检验。

非参数检验局限性：

• 当样本量较少的时候，检验结果不够敏感，即使数据分布有一定的偏离也不一定能检验出来
• 当样本量较大的时候，检验结果又会太多敏感，只要数据稍微有一点偏离，P值就会<0.05，检验结果倾向于拒绝原假设，认为数据不服从高斯分布

S-W检验：适用于小样本数据集，样本量≤5000

K-S检验：适用于大样本数据集，样本量>5000

做数据特征分析的时候，每个特征是否需要分别做正态性检验？

待补充

检验数据是否服从高斯分布策略：

        检验数据是否服从高斯分布方法有图示法(直方图、Q-Q图)和S-W检验、K-S检验。首选方法是图示法，即利用直方图、Q-Q图进行观察，如果分布严重偏态(左偏/右偏)和尖峰分布则建议进行假设检验。在样本量较小的时候优先选择S-W检验，反之使用K-S检验。统计学上一般P值大于0.05我们可认为该组数据是符合高斯分布。

import pandas as pd
from scipy import stats
#分布检验
def check(inX):
    results = []
    for j in range(inX.shape[1]):
        if inX.shape[0]<=5000:#S-W检验：小样本：≤5000
            statistics, p = stats.shapiro(inX.iloc[:,j])
        else:#K-S检验：大样本：>5000
            statistics, p = stats.kstest(inX.iloc[:,j], 'norm')
        results.append([statistics, p])
    print('shapiro, 统计量：%s，P值：%s' % (statistics, p))
    return results

if __name__=='__main__':
    # ******加载数据集**********
    trainData = 'testSet.txt'  # testSet.txt/secom.data/ex00.txt,ex0~9.txt
    baseData = pd.read_csv('./Data/'+trainData,sep='\t',names=['X1','X2','label'])
    #数据预处理


    # draw(baseData)
    QQfig(baseData)

    data1 = baseData[baseData['label'] > 0].iloc[:, :-1]
    data2 = baseData[baseData['label'] <0].iloc[:, :-1]
    check(data1)

非高斯分布转换为高斯分布

        为了使我们的数据趋向高斯分布，我们首先需要使数据对称，即消除偏度。为了消除偏度，我们要对数据进行转换：

       以下总结摘自博客机器学习中的特征分布_TianCMCC的博客-CSDN博客_特征分布

1. 对数变换： 对于高度偏态（如Skewness为其标准误差的3倍以上）的数据分布，我们则可以对其取对数处理。其中又可分为自然对数和以10为基数的对数，其中以10为基数的对数处理纠偏力度最强，但有时会矫枉过正，将正偏态转换成负偏态。

   

2. 平方根变换：平方根变换使服从泊松（Poisson）分布的样本或具有轻度偏态的样本正态化，或者是当各样本的方差与均数呈正相关时，使用平方根变换可使其达到方差齐性。

   

3. 倒数变换：常用于分布两端波动较大的数据，倒数变换可使极端值的影响减小

   

4. 平方根反正旋变换：常用于服从二项分布 或 百分比的数据。一般认为等总体率较小（如＜30%时）或较大（如＞70%时），偏离正态较为明显，通过样本率的平方根反正玄变换，可使数据接近正态分布，达到方差齐性的要求。

   

5. BOX-COX变换：通常用于连续的响应变量不满足正态分布的情况。在一些情况下（特征分布的P值<0.003）上述方法（平方变换等）很难实现正态化处理，所以可以考虑使用Box-Cox转换，但是当P值>0.003时，使用两种方法均可，优先考虑普通的平方变换。（其中 λ \lambdaλ 为待定变换参数）
    

高斯分布与聚类之GMM

        高斯混合混合模型(GMM)是一种概率生成模型，模型通过学习先验分布后推导后验分布来实现聚类。当我们做聚类任务的时候，可以根据距离最近原则，将样本聚类到距离其最近的聚类中心，如k-means算法，或者将样本聚类到距离某个簇边缘最近的簇，如DBSCAN算法，而GMM是假设样本每个类的特征分布遵循高斯分布，即整个数据集可由不同参数的高斯分布线性组合来描述，GMM算法可以计算出每个样本属于各个簇的概率值并将其聚类到概率值最大的簇。

GMM如何实现？

        GMM是以假设数据各个类别的特征分布是高斯分布为基础，所以首要步骤就是先得到各个类别的概率分布密度函数参数，对于一元变量，需要计算各个类别的均值和期望，而对于多元变量，则需要计算均值和协方差矩阵。有如下数据集X，共有m个样本，n项特征，k个类别

 高斯概率分布密度函数公式如下：

 一元变量：n=1

  多元变量：n>1

 式中，表示协方差矩阵，n行n列矩阵，表示计算第k个类别的协方差矩阵的行列式。注意，多元高斯概率分布密度函数涉及求逆过程，当协方差矩阵为奇异矩阵时，不可求逆。出现不可求逆的情况一般有两种：

1. 样本数量m<特征数量n
2. 样本存在冗余特征(线性相关)

现有如下数据集，如何使用GMM聚类？

在学习GMM聚类算法前，先从大学概率论课本上的一个例子入手。

例如：投掷一颗骰子，实验的样本空间为：S={1,2,3,4,5,6}。

存在以下事件

• 事件X={投掷一个骰子出现i点}，
• 事件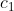={投掷一个骰子出现偶数点}，
• 事件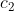= {投掷一个骰子出现奇数点}，

是样本空间S的一个划分，每做一次实验时，事件必有一个且仅有一个发生。则有

证明过程如下：

则事件X={投掷一个骰子出现i点}的概率p(X)为

  式中的称为先验概率，进一步得到以下公式：贝叶斯公式 

综上我们可以得到，投掷一颗骰子后，发生事件的概率为 

回到聚类任务中，上述 事件X={投掷一个骰子出现i点}其实就是我们的训练集对应X，事件

就是类别，对应y。如下所示：

p(X)是训练集样本出现的概率，公式如下：

GMM代价函数

         GMM首先需要计算每个类别的分布函数的参数，如何估计参数呢？可以采用极大似然估计方法。

        极大似然估计，就是利用已知的样本信息，反推最具有可能(最大概率)导致这些样本出现的模型参数值。换句话说，极大似然估计提供了一种通过给定观察数据来估计模型参数的方法，即：模型已定，参数未知。可以这样理解，既然事情(样本)已经发生了，为什么不让这个结果出现的可能性最大呢？这也就是极大似然估计核心。

        通过极大似然估计方法来使样本出现的概率p(X)最大从而得到分布函数参数，这样我们可以得到代价函数

 由于连乘可能会导致下溢，所以需要取对数。对数函数是一个严格递增的函数，取对数后不会改变数据的相对关系，即对数化后，我们仍然可以获得具有相同临界点的最优化函数，代价函数如下所示

 已知多元变量的高斯分布公式如下

可以得到

注意，式中  ，这里直接用概率分布密度函数表示概率分布可能有一定误导性。为什么这样表达呢？如下

 是每个类的一个常量乘法因子，在之后的对后验概率进行规范化的时候就抵消掉了。因此可以直接使用来估计类条件概率。

 综上，GMM代价函数的最终公式如下

           通过求解代价函数，就可以得到各个类别的高斯分布函数参数，进而能计算样本属于某个类别的概率，从而实现聚类，公式如下

 以上过程其实就是一个建模过程，建模过程包括如下

1. 分析业务类型(聚类问题)，√
2. 确定模型类型(参数+概率+生成模型)，√
3. 确定代价函数，√
4. 目标函数：超参数
5. 优化模型：调参

        在得到代价函数后，我们还要确定这个代价函数是否具有凸性，因为凸函数有一个好性质，若代价函数是凸函数，则其局部最优解也是全局最优解。若无法得到凸代价函数，则尝试更换模型或者使用迭代算法来逼近全局最优解。

目标函数一般是代价函数+正则项，用来确定超参数，防止过拟合，使结构风险最小，来提高模型泛化能力。本文这里先跳过这一步，直接讲如何计算参数。

使用EM算法计算GMM参数

        EM(期望最大)算法是一个迭代算法，其思想就是多次迭代来估计参数，直到算法收敛。EM算法就是一个迭代逼近过程，若目标函数为非凸函数，则EM算法不能保证收敛至全局最优解，且EM算法的求解结果与初值的选择有较大关系，该算法对初值敏感。

        EM算法求解参数思路可以将其理解为对两个未知变量的方程求解。首先固定其中一个未知数，求另一个未知数的偏导数，之后再反过来固定后者，求前者的偏导数，反复迭代直到目标函数值不变、收敛。EM算法就是相互迭代，求出一个稳定值，用于在无法直接找到参数的情况下寻找模型的最大似然估计(MLE)。它包括两个步骤:期望步骤和最大化步骤。在聚类问题中，步骤如下

1. 初始化参数：混合高斯分布函数参数
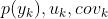
2. 根据估计的参数计算簇成员后验概率：
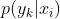
3. 最大化步骤：代价函数代入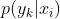，求参数偏导，更新每一个参数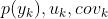
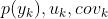   (分别可以只用一个未知量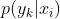来表达)
4. 重复1、2步骤直到对数似然值收敛。 

 具体步骤如下

1、初始化参数，根据估计参数计算给定数据点属于类别的概率(后验概率)：

2、最大化步骤：根据第一步得到的，对代价函数求偏导来更新每一个参数,

 3、重复1、2步骤，直到算法收敛。

参数推导过程 

        可通过对代价函数求偏导得到，过程比较复杂，所以本文从另一个角度来解释参数的计算过程。

关于均值μ：

 

 

 关于协方差矩阵如何计算：给定如下训练集X:m*2，假设有k个类别，则

        GMM的代价函数是最大化数据X出现的概率p(X)。若多次迭代后的p(X)保持不变，则说明程序已收敛。在得到参数，即得到数据集每个类别的概率分布函数，就可以计算每个样本属于各个类别的概率，样本选择最大的概率值对应的聚类中心，从而实现聚类。

GMM算法优缺点

优点：

        GMM假设生成数据的是一种混合的高斯分布，为模型找到最大似然估计。与将数据点硬分配到聚类的K-means方法（假设围绕质心的数据呈圆形分布）相比，它使用了将数据点软分配到聚类的方法（即概率性，因此更好）。速度：它是混合模型学习算法中的最快算法;无偏差性：由于此算法仅最大化可能性，因此不会使均值趋于零，也不会使聚类大小具有可能适用或不适用的特定结构。
（A）通过使用软分配捕获属于不同聚类的数据点的不确定性，

（B）对圆形聚类没有偏见。即使是非线性数据分布，它也能很好地工作，具有较强的鲁棒性

缺点：

• 奇异性：当每个混合模型的点数不足时，估计协方差矩阵将变得困难，并且除非对协方差进行人为正则化，否则该算法会发散并寻找无穷大似然函数值的解。GMM:需要求逆

• 适合聚类球状类簇，不能发现一些混合度较高，非球状类簇

• 需要指定簇个数

高斯分布与异常检测

        数据集中的异常数据一般包括异常点、离群点，特点时这些数据的特征与大多数数据不一致，呈现出"异常"的特点，检测这些数据的方法称为异常检测。异常检测也可看成是不平衡类数据下的分类问题。检测异常值对于几乎所有定量学科（即：物理、经济、金融、机器学习、网络安全）都非常重要。在机器学习和任何定量学科中，数据质量与预测或分类模型的质量一样重要。

异常检测算法使用场景

什么时候我们需要异常点检测算法呢？常见的有三种情况。 

1. 在做特征工程的时候需要对异常的数据做过滤，防止对归一化等处理的结果产生影响
2. 对没有标记输出的特征数据做筛选，找出异常的数据
3. 有标记输出的特征数据做二分类时，由于某些类别的训练样本非常少，类别严重不平衡，此时也可以考虑用非监督的异常点检测算法来做

异常点检测算法常见类别

异常点检测的目的是找出数据集中和大多数数据不同的数据，常用的异常点检测算法一般分为三类

• 基于统计学的方法来处理异常数据：这种方法一般会构建一个概率分布模型，并计算对象符合该模型的概率，把具有低概率的对象视为异常点。
• 基于聚类的方法来做异常点检测：由于大部分聚类算法是基于数据特征的分布来做的，通常如果我们聚类后发现某些聚类簇的数据样本量比其他簇少很多，而且这个簇里数据的特征均值分布之类的值和其他簇也差异很大，这些簇里的样本点大部分时候都是异常点。例如：DBSCAN
• ......

基于高斯分布的异常检测

        使用高斯分布来开发异常检测算法，需要假设数据是高斯分布的(这个假设不能适用于所有数据集)。

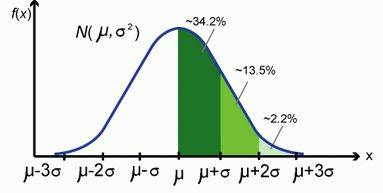
高斯分布3σ原则

        假设原数据服从某个分布(如高斯分布)，然后计算均值和方差，再计算[μ-3σ,μ-3σ]的区间，最后落在区间之外的数据点就被认为是异常值，即落在尾部分布的数据概率很小了，几乎不可能出现；但是出现了，所以是异常的。

多元高斯分布异常检测思路

        给定一个m*n维训练集，将训练集转换为n维的高斯分布，通过对m个训练样例的分布分析，得出训练集的概率密度函数，即得出训练集在各个维度上的数学期望μ和方差σ^2，并且利用少量的验证集来确定一个阈值ε。当给定一个新的点，我们根据其在高斯分布上算出的概率，及阈值ε，判断当p<ε判定为异常，当p>ε判定为非异常。

关于ε的确定，我们需要部分已知结果的训练样例作为验证集。在训练过程中，尝试多种ε的值，然后根据F1 Score来选择ε的值。

存在问题

•  均值和方差都对异常值很敏感，在实际计算的时候，异常值也被包含在全部数据集里。
• 对于存量数据，通过统计假设检验可以一次性找出其中的高风险交易。但是对于风控从业人员来讲，业务和指标上并不允许你有足够的时间和容忍度直到高风险金额累积到显著之后再进行判别，除非你KPI不想要了: )

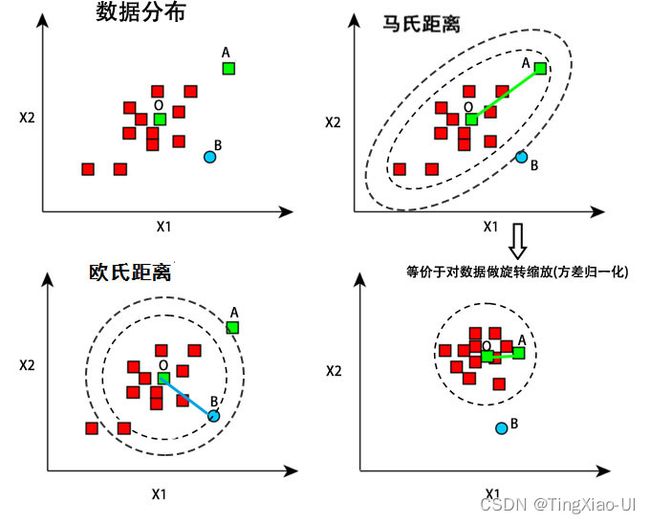
高斯分布与马氏距离

现有如下数据集，计算某两个样本之间的距离

​欧式距离:

​马氏距离:

​  ​是协方差矩阵求逆。当​为单位矩阵时，马氏距离==欧式距离。

欧氏距离与马氏距离的不同点在于欧式距离没有考虑

1. 特征尺度(量纲)不同
2. 特征分布情况
3. 特征线性相关情况

针对第一种情况，可以在训练模型前对数据做归一化处理，把各维特征都缩放到同一个标准时，使各维具有可比性。然后在使用欧式距离计算。

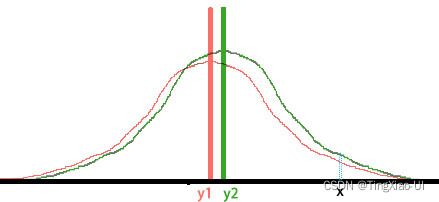
至于第二情况下，如下图所示，各维特征同分布但方差不同，如果用欧式距离计算，会认为x到y2和的距离比到y1更近，然后把x归类到y2中，但如果我们结合数据分布情况和如高斯分布的3σ原则的话，x更应该归类到y1才合理。

​

至于第三情况下，如下图所示，各维度分布相同但不独立，线性相关，如果如果用欧式距离计算，很难将x准确归类

​

而马氏距离主要做两个操作

• 解决维度分布差异(方差不同)和量纲不同的问题：方差归一化，对应于​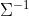矩阵的对角元素
• 解决维度存在的线性相关问题：旋转变换，对应于​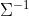矩阵的非对角元素

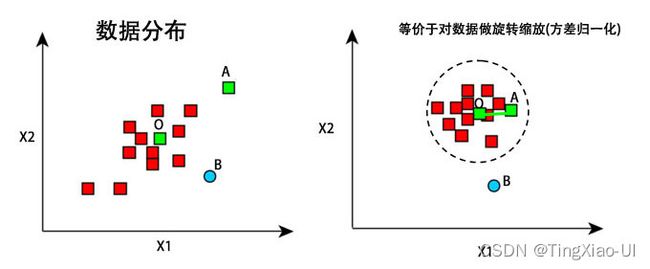
 如下图所示

​

​

         可以看到在考虑各维度特征的分布情况以及特征之间线性相关情况下，A点与O点的距离更近，这样也更合理。

        也这样直观理解，马氏距离策略是从椭圆中心到椭圆上各点的距离相同，而欧氏距离的策略是圆心到圆各点的距离相同。

​

欧式距离是假设各维特征间分布情况相同、独立且尺度相同。马氏距离是欧氏距离的泛化，马氏距离就是对数据做旋转缩放变换，相当于做了方差归一化后在计算欧氏距离。

 协方差的作用

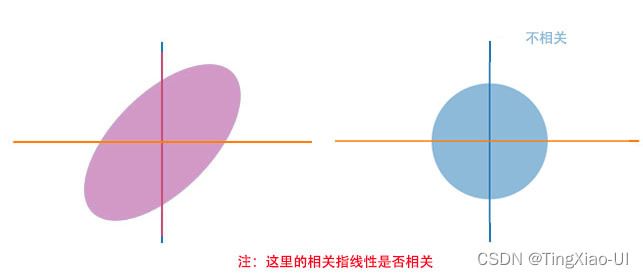
假设数据集是二维变量X，Y，数据分布如下图所示，反映了变量X与变量Y之间的线性相关关系。

​

一般情况下，如果想知道两个随机变量之间的关系，可以利用协方差矩阵，计算相关矩阵系数来得出它们之间的关系，若相关矩阵系数为0，则它们之间的线性不相关的，若相关矩阵系数>0，则它们呈正相关的关系，若相关矩阵系数<0，则它们呈负相关系数。

当数据集是多维变量时，用协方差矩阵衡量变量之间的线性相关性，协方差矩阵可以表示为如下

​

多元高斯分布与马氏距离的关系

 多元高斯分布公式：

​

 马氏距离公式：

​

待补充