傅里叶变换、短时傅里叶变换和小波变换的概述
这篇文章首先介绍点的概念,从简单的点到复杂的点,讲解如何用基表示这些点。然后再从复杂的点到函数,引出傅里叶分析,并介绍了傅里叶变换的优缺点,根据其缺点提出改进措施。
文章目录
-
- 一、点的概念
-
- 1.1 一个简单的点
- 1.2 基
- 1.3 函数
- 二、傅里叶分析
- 三、短时傅里叶变换STFT
- 四、小波变换
-
- 4.1 小波变换的应用
一、点的概念
1.1 一个简单的点
点在一个直线上可以表示为一个数,在二维平面上可以表示为 x + j y = α e j φ x + jy = \alpha {e^{j\varphi }} x+jy=αejφ。在实数的n维空间中,可以表示为 [ x 1 , x 2 , … , x n ] T {[{x_1},{x_2}, \ldots ,{x_n}]^T} [x1,x2,…,xn]T。当有很多点的时候,用上述方式就不太可行了。我们希望用少量的资源,表示出所有的点。那么,如何做呢?
1.2 基
大家应该都听过基这个名字。那为什么要有基的概念呢?
基:就是用更少的资源,表示全部。
平凡基(一般坐标系): p 1 = [ 1 , 0 , … , 0 ] T , p 2 = [ 0 , 1 , … , 0 ] T , ⋯ , p n = [ 0 , 0 , … , 1 ] T p_{1}=[1,0, \ldots, 0]^{T},p_{2}=[0,1, \ldots, 0]^{T}, \cdots, p_{n}=[0,0, \ldots, 1]^{T} p1=[1,0,…,0]T,p2=[0,1,…,0]T,⋯,pn=[0,0,…,1]T 空间中任意点,都可以用这个坐标表示。
举个栗子,现有一点的坐标是 [ 1 , 2 , 3 ] T [1,2,3]^{T} [1,2,3]T,这个就是又上面 n = 3 n=3 n=3的平凡基构成的。如果,我想要用更少的资源去表示这个点,我只需要将平凡基换成 p 1 = 1 14 [ 1 , 2 , 3 ] T , p 2 = 1 5 [ − 2 , 1 , 0 ] T , p 3 = 1 47 [ 3 , 6 , − 5 ] T p_{1}=\frac{1}{\sqrt{14}}[1,2,3]^{T}, \quad p_{2}=\frac{1}{\sqrt{5}}[-2,1,0]^{T}, \quad p_{3}=\frac{1}{\sqrt{47}}[3,6,-5]^{T} p1=141[1,2,3]T,p2=51[−2,1,0]T,p3=471[3,6,−5]T(其中 p 1 , p 2 , p 3 p_{1},p_{2},p_{3} p1,p2,p3是正交的,改变的基不唯一哦)。因此,在这个新基下,同一空间中的点可以表示为 [ 14 , 0 , 0 ] T [\sqrt{14},0,0]^{T} [14,0,0]T。这样,我们就将3个数表示的点变成了1个数。看下图,可以更加直观的感受。
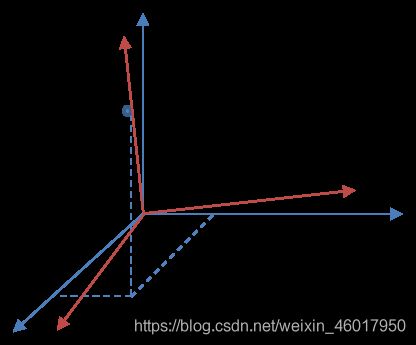
(蓝色是平凡基,红色是修改后的基)
1.3 函数
这里给出另一个角度来理解函数。将上面介绍的有限维的点 p ( x 1 , x 2 , … , x n ) p(x_{1},x_{2},\ldots,x_{n}) p(x1,x2,…,xn)左右延伸,变成 p ( … , x − 1 , x 0 , x 1 , … ) p(\ldots,x_{-1},x_{0},x_{1},\ldots) p(…,x−1,x0,x1,…)无限维,这时无数点联合起来就变成了一个函数。函数又分为周期函数和非周期函数。
二、傅里叶分析
从函数的角度出发,如何用上面谈到的基来表示任意复杂函数呢?Fourier在1807年提出傅里叶级数。 f ( t ) = ∑ k = − ∞ + ∞ α k e i k t f(t)=\sum_{k=-\infty}^{+\infty} \alpha_{k} e^{i k t} f(t)=∑k=−∞+∞αkeikt,只有确定系数 α k {\alpha _k} αk,该函数就可以表达出来了。
意义:
1)不同函数的差异就体现在系数 α k {\alpha _k} αk上。
2)对不同特点的函数的分析,可以选择不同的基。
缺点:
对于随着时间变换的非平稳信号,它没法区分频谱。只能获取一段信号总体上包含哪些频率的成分,但是对各成分出现的时刻并无所知。因此时域相差很大的两个信号,可能频谱图一样。
解决办法:
所以,这里提出两种解决办法。①加入局部参数,比如加窗。②换基。
关于傅里叶级数和傅里叶变换的具体公式推导总结,见https://blog.csdn.net/weixin_46017950/article/details/114691667。
三、短时傅里叶变换STFT
方法一:加窗。
STFT在傅里叶变换的基础上加窗,分段做FFT变换,假定认为信号在窗宽度的时间内是平稳的。但是,窗宽度太窄,信号太短信息少,频率分析不准确,频率分辨率差;窗太宽时间分辨率差。对于时变的非稳态信号,高频适合小窗口,低频适合大窗口。(高频,顾名思义就是信号变化很快,所以,在时域中,需要小窗口,时间分辨率高。)然而STFT的窗口是固定的,在一次STFT中宽度不会变化,所以STFT还是无法满足非稳态信号变化的频率的需求。不采用可变窗的STFT,是因为这样做冗余会太严重,STFT做不到正交化,这也是它的一大缺陷。
四、小波变换
方法二:换基。
何为小波呢?“小”是指衰减性,比如有些小波基只有局部是非零,这也称为紧支性。“波”是指波动性。
小波变换直接把傅里叶变换的基给换了——将无限长的三角函数基换成了有限长的会衰减的小波基。这样不仅能够获取频率,还可以定位到时间,获取时频分析。目标:时间分辨率和频率分辨率可以随着本身信号特变进行自适应调整。这里的“自适应”是很难的。
W T ( a , b ) = 1 a ∫ − ∞ ∞ f ( t ) ∗ ψ ( t − b a ) d t W T(a, b)=\frac{1}{\sqrt{a}} \int_{-\infty}^{\infty} f(t) * \psi\left(\frac{t-b}{a}\right) d t WT(a,b)=a1∫−∞∞f(t)∗ψ(at−b)dt
小波还有一些好处,比如,我们知道对于突变信号,傅里叶变换存在吉布斯效应,我们用有限长的频率信号是怎么也拟合不好突变信号的。
JPEG2000压缩就是用正交小波变换。比如典型的正交基:二维笛卡尔坐标系的(1,0)、(0,1),用它们表达一个信号显然非常高效,计算简单。而如果用三个互成120°的向量表达,则会有信息冗余,有重复表达。但是并不意味着正交一定优于不正交。比如,如果是做图像增强,有时候反而希望能有一些冗余信息,更利于对噪声的抑制和对某些特征的增强。
4.1 小波变换的应用
1、数据压缩。目前许多应用领域(如卫星监测、地震勘探、天气预报)都存在海量数据传输或存储问题,如果不对数据进行压缩,数量巨大的数据就很难存储、处理和传输。因此,伴随小波分析的诞生,数据压缩一直是小波分析的重要应用领域之一,并由此带来巨大的经济效益和社会效益。
2、语音分析与处理。小波理论应用于语音分析与处理的主要内容包括:清/浊音分割;基音检测与声门开启时刻定位;去噪、压缩、重建几个方面。
3、瞬态信号或图像的突变点常包含有很重要的故障信息,例如,机械故障、电力系统故障、脑电图、心电图中的异常、地下目标的位置及形状等,都对应于测试信号的突变点。因此,小波分析在故障检测和信号的多尺度边缘特征提取方面的应用具有广泛的应用前景。
4、神经网络与小波分析相结合,分形几何与小波分析相结合是国际上研究的热点之一。基于神经网络的智能处理技术,模糊计算、进化计算与神经网络结合的研究,没有小波理论的嵌入很难取得突破。非线性科学的研究正呼唤小波分析,也许非线性小波分析是解决非线性科学问题的理性工具。
下一篇文章写一写小波变换在图像方面的分析与应用(Matlab代码)。