层次分析法(AHP)的Python实现方式
层次分析法是数学建模最基础的模型之一,主要用于解决评价类问题。
解决评价类问题,应首先考虑以下三个问题:①我们评价的目标是什么②我们达到目标有哪几种具体方案③评价的准则或者是指标是什么
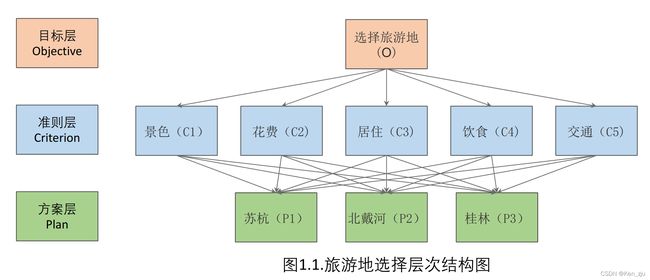
引一例题:小明想要去旅游(评价目标),初步选择苏杭、北戴河、桂林三地(具体方案),第三个问题则经常通过题目中的背景材料、常识or相关文献整理而来,这里假定小明选择了五个评判指标(如景色、消费水平等五种)。
第一步,我们绘制层次结构图,可以利用PPT的SmartArt或者亿图图示来生成。
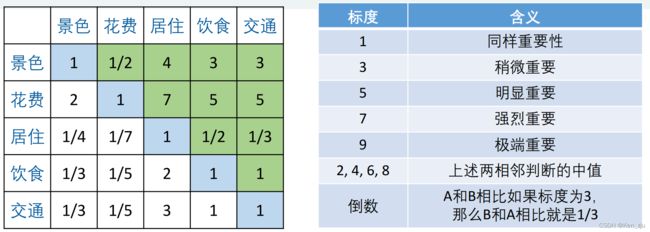
第二步,对于整个准则层以及单个准则对应下的方案层进行两两比较,形成判断矩阵。(严格意义中应该由专家进行填写)
同理,对于每个准则下的所有具体方案进行两两比较评判。
第三步,判断矩阵由于主观性,往往会出现A>B,B>C,按理说应满足A>C却在表格中出现C>A的情况,因此所有判断矩阵需要进行一致性检验(即各行or各列应该是满足等比例的)。下面直接进入代码实现部分。
import numpy as np
# 一致性检验函数
def consistency_test(A):
eigen = np.linalg.eig(A)[0] #eig函数返回矩阵的特征值和特征向量
n = A.shape[0]
CI = (max(eigen) - n) / (n - 1)
RI = [0,0, 0.52, 0.89, 1.12, 1.26, 1.36, 1.41, 1.46, 1.49, 1.52, 1.54, 1.56, 1.58, 1.59]
CR = CI / RI[n - 1]
CI = float(CI)
CR = float(CR)
print('The CI is:{}'.format(CI))
print('The CR is:{}'.format(CR))
if CR < 0.1:
print('一致性检验通过')
return 1
else:
print('一致性检验未通过')
return 0 # 对CR进行判断,用于下面计算权重函数。第四步,通过判断矩阵计算权重,主要有算术平均、几何平均、特征值三种方法。为了保证结果的稳健性,建议在论文中使用三种方法分别计算。代码部分如下:
# 计算权重函数
def count(A):
q = consistency_test(A)
n = A.shape[0]
while q: #一致性检验通过
weight1 = (np.sum(A / np.sum(A, axis=0), axis=1)) / n # 算术平均权重
weight2 = pow(np.prod(A, axis=1), 1 / n) / np.sum(pow(np.prod(A, axis=1), 1 / n)) # 几何平均权重
eigen, F_vector = np.linalg.eig(A) #返回特征向量和特征值
for i in range(n):
if eigen[i] == np.max(eigen):
index_e = i
best = F_vector[:, index_e]
weight3 = best / np.sum(best) # 特征值权重
print(weight1, '\n', weight2, '\n', weight3, '\n')
return weight1, weight2, weight3
else:
print('请调整判断矩阵')第五步,根据权重矩阵计算得分,也可以利用Excel表中的函数orpython快速计算,最后进行排序得出。让我们来看看结果吧:
# 数据获取与处理
tx = open('data.txt').readlines()
tx得到六行,六个矩阵的ravel版(当然用pd.read也行啦):
把每行的矩阵进行重组,形成正常的六个矩阵:
for i in range(len(tx)):
tx[i] = np.array(list(eval(tx[i])))
n0 = int((np.size(tx[i])) ** 0.5)
tx[i] = tx[i].reshape(n0, n0)接下来就是代入函数去实现,得出结果。读者可以自行去尝试实现。
代码不足:n=1或者2的时候除数会出现0,如何处理?
python小数点的计算误差如何处理?
AHP只适用于特征值不多的评价问题,比如十来个,多了怎么处理?
本文主体思路借鉴某视频,侵权即删。