《剑指offer》题解——week1(持续更新)
❤ 作者主页:Java技术一点通的博客
❀ 个人介绍:大家好,我是Java技术一点通!( ̄▽ ̄)~*
❀ 微信公众号:Java技术一点通
记得点赞、收藏、评论⭐️⭐️⭐️
认真学习!!!
《剑指offer》题解——week1
- 一、剑指 Offer 03. 数组中重复的数字
-
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 二、剑指 Offer 04. 二维数组中的查找
-
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 三、 剑指 Offer 05. 替换空格
-
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 四、剑指 Offer 06. 从尾到头打印链表
-
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 五、剑指 Offer 07. 重建二叉树
-
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 六、剑指 Offer 09. 用两个栈实现队列
-
- 1.题目描述
- 2. 思路分析
- 3. 代码实现
- 七、剑指 Offer 10- I. 斐波那契数列
-
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 八、剑指 Offer 10- II. 青蛙跳台阶问题
-
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 九、剑指 Offer 11. 旋转数组的最小数字
-
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 十、剑指 Offer 12. 矩阵中的路径
-
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
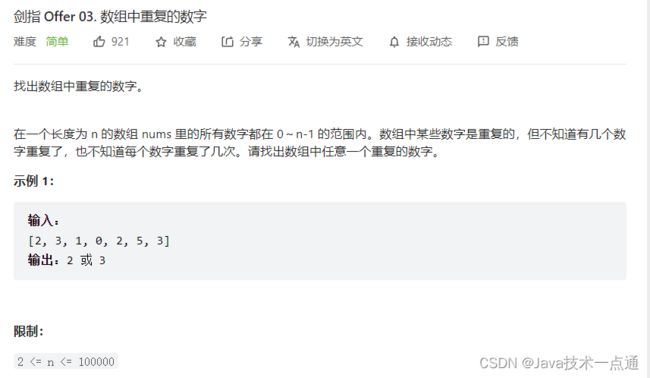
一、剑指 Offer 03. 数组中重复的数字
1. 题目描述
2. 思路分析
方法一:哈希表
思路:定义一个哈希表,遍历一次数组,利用哈希表对每个元素进行标记。若当前元素被标记过了,则该元素重复。
时间复杂度:O(n)
方法二:原地交换
主要思想是把每个数放到对应的位置上,即让 nums[i] = i。
前往后遍历数组中的所有数,假设当前遍历到的数是 nums[i]=x,那么:
- 如果
x != i && nums[x] == x,则说明x出现了多次,直接返回x即可; - 如果
nums[x] != x,那我们就把x交换到正确的位置上,即swap(nums[x], nums[i]),交换完之后如果nums[i] != i,则重复进行该操作。由于每次交换都会将一个数放在正确的位置上,所以swap操作最多会进行n次,不会发生死循环。
循环结束后,如果没有找到任何重复的数,则返回-1。
时间复杂度:
每次swap操作都会将一个数放在正确的位置上,最后一次swap会将两个数同时放到正确位置上,一共只有n个数和n个位置,所以swap最多会进行n−1次。所以总时间复杂度是O(n)。
3. 代码实现
方法一:
class Solution {
public:
int findRepeatNumber(vector& nums) {
for (auto x : nums)
if (x < 0 || x >= n)
return -1;
unordered_map mp;
for (int num : nums) {
if (mp[num]) return num;
mp[num] = true;
}
return -1;
}
};
方法二:
class Solution {
public:
int duplicateInArray(vector& nums) {
int n = nums.size();
for (auto x : nums)
if (x < 0 || x >= n)
return -1;
for (int i = 0; i < n; i ++ ) {
while (nums[nums[i]] != nums[i]) swap(nums[i], nums[nums[i]]);
if (nums[i] != i) return nums[i];
}
return -1;
}
};
二、剑指 Offer 04. 二维数组中的查找
1. 题目描述
2. 思路分析
利用矩阵 “从上到下递增、从左到右递增” 的特点。
- 从矩阵 matrix 左下角元素(索引设为 (i, j) )开始遍历,并与目标值对比:
- 当
matrix[i][j] > target时,执行i--,即消去第i行元素; - 当
matrix[i][j] < target时,执行j ++,即消去第j列元素; - 当
matrix[i][j] = target时,返回true,代表找到目标值。
- 若行索引或列索引越界,则代表矩阵中无目标值,返回
false。
时间复杂度O(M+N):其中,N和M分别为矩阵行数和列数,此算法最多循环M+N次。
3. 代码实现
class Solution {
public:
bool findNumberIn2DArray(vector>& matrix, int target) {
int i = matrix.size() - 1, j = 0;
while (i >= 0 && j target) i --;
else if (matrix[i][j] < target) j ++;
else return true;
}
return false;
}
};
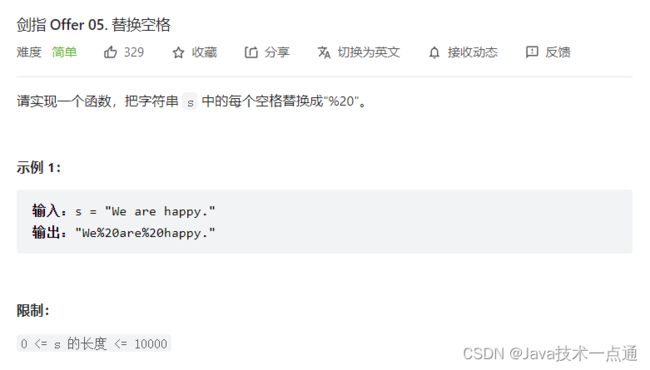
三、 剑指 Offer 05. 替换空格
1. 题目描述
2. 思路分析
从前往后依次枚举原字符串:
- 如果遇到空格,则在
string类型的答案res中添加"%20"; - 如果遇到其他字符,则直接将它添加在答案中;
时间复杂度:O(n)
3. 代码实现
class Solution {
public:
string replaceSpace(string s) {
string res;
for (auto c : s) {
if (c == ' ') res += "%20";
else res += c;
}
return res;
}
};
四、剑指 Offer 06. 从尾到头打印链表
1. 题目描述
2. 思路分析
单链表只能从前往后遍历,不能从后往前遍历。
因此我们先从前往后遍历一遍输入的链表,将结果记录在答案数组中。
最后再将得到的数组逆序即可。
时间复杂度:链表和答案数组仅被遍历了常数次,所以总时间复杂度是 O(n)。
3. 代码实现
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
vector reversePrint(ListNode* head) {
vector res;
while (head) {
res.push_back(head->val);
head = head->next;
}
return vector(res.rbegin(), res.rend());
}
};
五、剑指 Offer 07. 重建二叉树
1. 题目描述
2. 思路分析
重构一颗二叉树:(pl,pr,il,ir)
含义:这棵树的先序遍历结果为(pl, pr)(preorder中下边位置),中序遍历结果为(il, ir)。
- 先序遍历的第一个结果就是“树根”;
- 在对应的中序遍历中找到该树根所在的位置下标:
i(左右子树中序遍历结果的分界点); - 根的左子树的节点数目为:
nl(i - il); - 剩余结点为右子树;
- 递归调用左右子树。
3. 代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector preorder, inorder;
map mp;
TreeNode* buildTree(vector& _preorder, vector& _inorder) {
preorder = _preorder, inorder = _inorder;
for(int i = 0; i < inorder.size(); i ++ ) mp[inorder[i]] = i;
return dfs(0, preorder.size() - 1, 0, inorder.size() - 1);
}
TreeNode* dfs(int pl, int pr, int il, int ir){
if(pl > pr) return NULL;
TreeNode* root = new TreeNode(preorder[pl]);
int p = mp[preorder[pl]];
root->left = dfs(pl + 1, pl + 1 + p - il - 1, il, p - 1);
root->right = dfs(pl + 1 + p - il - 1 + 1, pr, p + 1, ir);
return root;
}
};
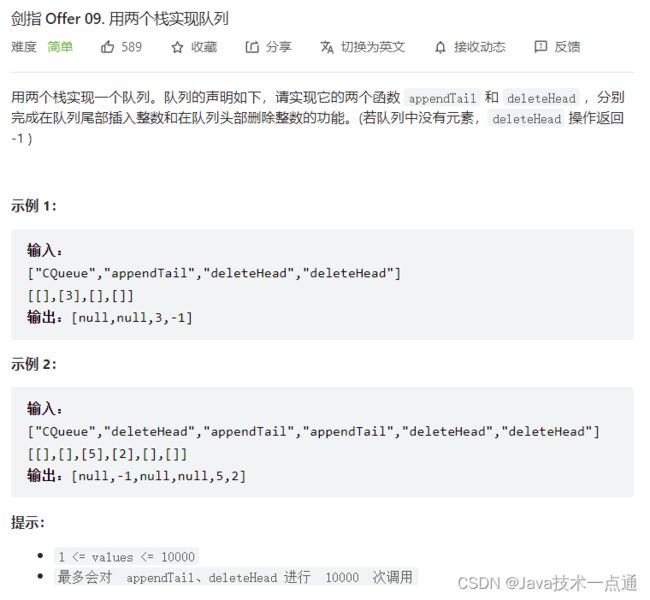
六、剑指 Offer 09. 用两个栈实现队列
1.题目描述
2. 思路分析
只使用一个栈stack1当作队列,另一个栈stack2用来辅助操作。
要想将stack1栈底的元素删除,需要将stack1的元素全部移到stack2,然后弹出stack2栈顶元素,最后将stack2的元素全部回到stack1。
3. 代码实现
class CQueue {
public:
stack stack1;
stack stack2;
CQueue() {
}
void appendTail(int value) {
stack1.push(value);
}
int deleteHead() {
if (stack1.empty()) return -1;
while (!stack1.empty()) {
int tmp = stack1.top();
stack1.pop();
stack2.push(tmp);
}
int res = stack2.top();
stack2.pop();
while (!stack2.empty()) {
int tmp = stack2.top();
stack2.pop();
stack1.push(tmp);
}
return res;
}
};
/**
* Your CQueue object will be instantiated and called as such:
* CQueue* obj = new CQueue();
* obj->appendTail(value);
* int param_2 = obj->deleteHead();
*/
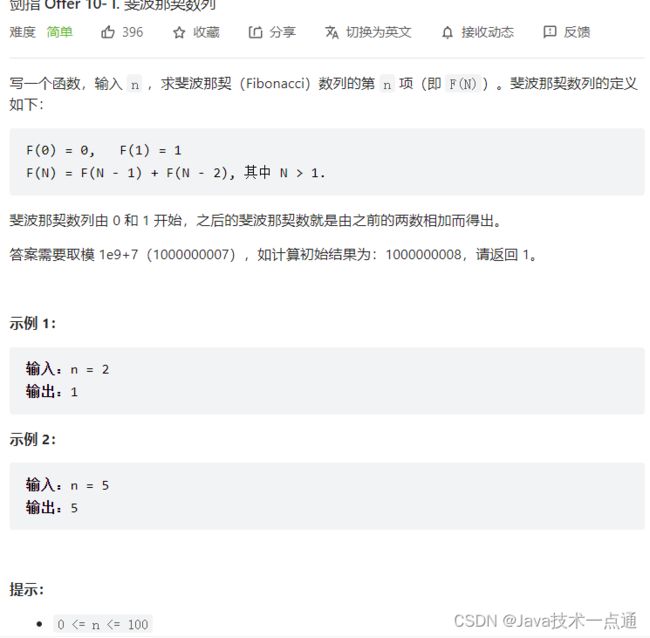
七、剑指 Offer 10- I. 斐波那契数列
1. 题目描述
2. 思路分析
动态规划是本题的最佳解法。
以斐波那契的性质f(n) = f(n - 1) + f(n - 2)作为转移方程。
3. 代码实现
class Solution {
public:
int fib(int n) {
if (n < 2) return n;
int f[n + 1];
f[0] = 0, f[1] = 1;
for (int i = 2; i <= n; i ++ ) {
f[i] = f[i - 1] + f[i - 2];
f[i] %= 1000000007;
}
return f[n];
}
};
八、剑指 Offer 10- II. 青蛙跳台阶问题
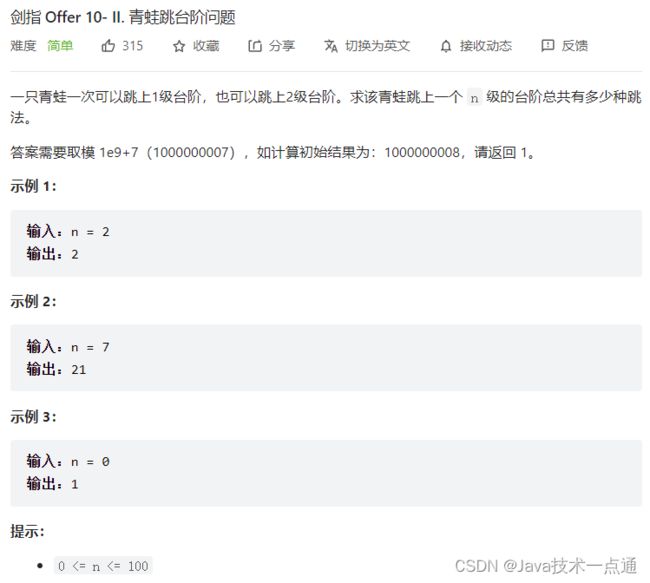
1. 题目描述
2. 思路分析
动态规划: f[i]表示上i级台阶的方案数,枚举最后一步是上1级台阶,还是上2级台阶,所以有: f[i]=f[i−1]+f[i−2]。
3. 代码实现
class Solution {
public:
int numWays(int n) {
if (n == 0) return 1;
vector f(n + 1);
f[0] = 1;
f[1] = 1;
for (int i = 2; i <= n; i ++ ) {
f[i] = (f[i - 1] + f[i - 2]) % 1000000007;
}
return f[n];
}
};
九、剑指 Offer 11. 旋转数组的最小数字
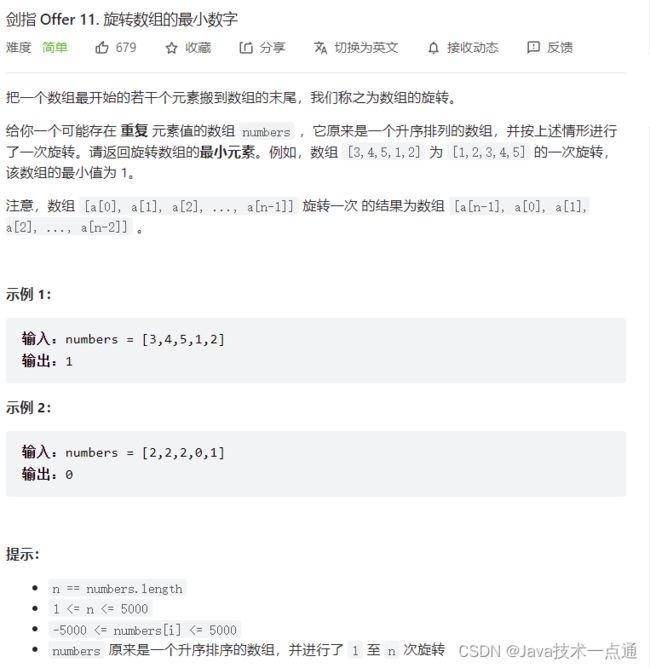
1. 题目描述
2. 思路分析
二分查找:
定义l,r两个指针,分别指向nums数组的左右两端。
令mid = (l + r) / 2,然后循环二分:
- 当
nums[mid] > nums[r]时:则mid一定指向旋转数组的左半部分,最小值一定在[mid + 1, r]闭区间中,因此执行l = mid + 1; - 当
nums[mid] < nums[r]时:则mid一定指向旋转数组的右半部分,最小值一定在[l, mid]闭区间中,因此执行r = mid; - 其余情况,可以通过
r = r - 1进行缩小范围。
3. 代码实现
class Solution {
public:
int minArray(vector& numbers) {
int l = 0, r = numbers.size() - 1;
while (l < r) {
int mid = (l + r) / 2;
if (numbers[mid] > numbers[r]) {
l = mid + 1;
} else if (numbers[mid] < numbers[r]) {
r = mid;
} else {
r --;
}
}
return numbers[l];
}
};
十、剑指 Offer 12. 矩阵中的路径
1. 题目描述
2. 思路分析
dfs:
在深度优先搜索中,最重要的就是考虑好搜索顺序。
我们先枚举单词的起点,然后依次枚举单词的每个字母。
过程中需要将已经使用过的字母改成一个特殊字母,以避免重复使用字符。
实现步骤:
- 如果
board[x][y] != word[k], 当前字符不匹配,直接返回false; - 如果当前已经访问到字符串的末尾,且对应字符依然匹配,此时直接返回
true。 - 否则,遍历当前位置的所有相邻位置。如果从某个相邻位置出发,能够搜索到子串
word[k + 1...],则返回true,否则返回false。
3. 代码实现
class Solution {
public:
bool exist(vector>& board, string word) {
for (int i = 0; i < board.size(); i ++ ) {
for (int j = 0; j < board[i].size(); j ++ ) {
if (dfs(board, word, 0, i, j)) return true;
}
}
return false;
}
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
bool dfs(vector>& board, string& word, int u, int x, int y) {
if (board[x][y] != word[u]) return false;
if (u == word.size() - 1) return true;
char t = board[x][y];
board[x][y] = '.';
for (int i = 0; i < 4; i ++ ) {
int a = x + dx[i], b = y + dy[i];
if (a < 0 || a >= board.size() || b < 0 || b >= board[0].size() || board[a][b] == '.') continue;
if (dfs(board, word, u + 1, a, b)) return true;
}
board[x][y] = t;
return false;
}
};
创作不易,如果有帮助到你,请给题解点个赞和收藏,让更多的人看到!!!
关注博主不迷路,内容持续更新中。