剑指Offer week 1
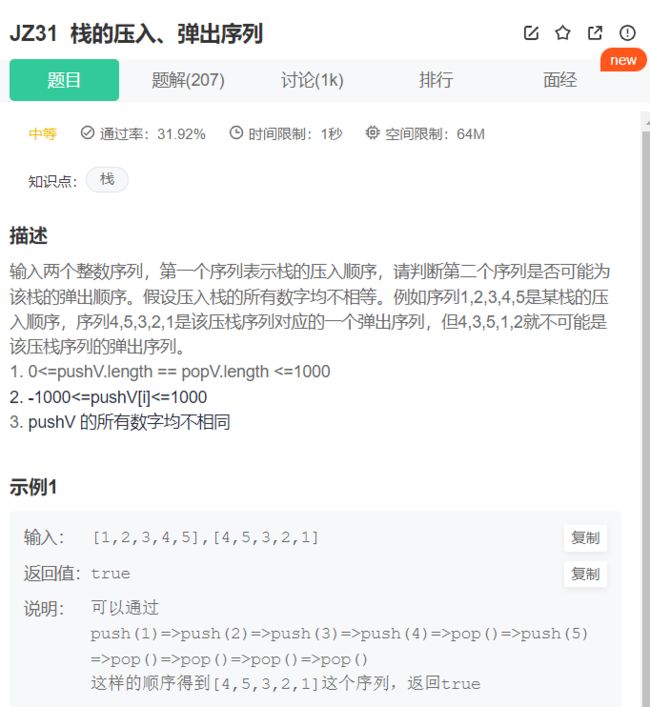
21.栈的压入、弹出序列
class Solution {
public:
bool IsPopOrder(vector<int> pushV,vector<int> popV) {
// 特判
if (pushV.empty() || popV.empty() || pushV.size() != popV.size()) return false;
stack<int> sk;
int len = pushV.size();
int popIndex = 0;
for (int i = 0; i < len; i++) {
sk.push(pushV[i]);
while (!sk.empty() && sk.top() == popV[popIndex]) {
sk.pop();
popIndex++;
}
}
if (sk.empty()) {
return true;
}
return false;
}
};
22.从上往下打印二叉树
正常思路,使用队列即可
class Solution {
public:
vector<int> PrintFromTopToBottom(TreeNode* root) {
if (!root) return vector<int>();
queue<TreeNode*> q;
q.push(root);
vector<int> ans;
TreeNode* node = nullptr;
while (!q.empty()) {
node = q.front();
q.pop();
ans.push_back(node->val);
if (node->left) q.push(node->left);
if (node->right) q.push(node->right);
}
return ans;
}
};
23.二叉搜索树的后序遍历序列
如果不会的话,画一个较大的二叉搜索树,后序遍历,跟着代码走一遍
class Solution {
public:
// 后序遍历二叉搜索树,可以通过大小来判断左右子树
bool VerifySquenceOfBST(vector<int> sequence) {
if (0 == sequence.size()) return false;
if (1 == sequence.size()) return true;
return check(sequence, 0, sequence.size() - 1);
}
bool check(vector<int>& sequence, int start, int end) {
if (start >= end) return true; // 若当前子树只有一个节点
int root = sequence[end]; // 当前子树根节点
// 排除右子树
int high = end - 1;
while (high >= 0 && sequence[high] > root) high--;
for (int i = 0; i <= high; i++) {
if (sequence[i] > root) return false;
}
// 分治 左右子树
return check(sequence, start, high) && check(sequence, high + 1, end - 1);
}
};
24.二叉树中和为某一值的路径(二)
class Solution {
public:
void FindPathCore(TreeNode* root, vector<vector<int>> &result, vector<int> tmp, int sumNum) {
if (!root) return;
tmp.push_back(root->val);
if (root->left == nullptr && root->right == nullptr && sumNum == root->val) {
result.push_back(tmp);
} else {
if (root->left) {
FindPathCore(root->left, result, tmp, sumNum - root->val);
}
if (root->right) {
FindPathCore(root->right, result, tmp, sumNum - root->val);
}
}
tmp.pop_back();
}
vector<vector<int>> FindPath(TreeNode* root,int expectNumber) {
if (!root) return vector<vector<int>> ();
vector<vector<int>> result;
vector<int> tmp;
FindPathCore(root, result, tmp, expectNumber);
return result;
}
};
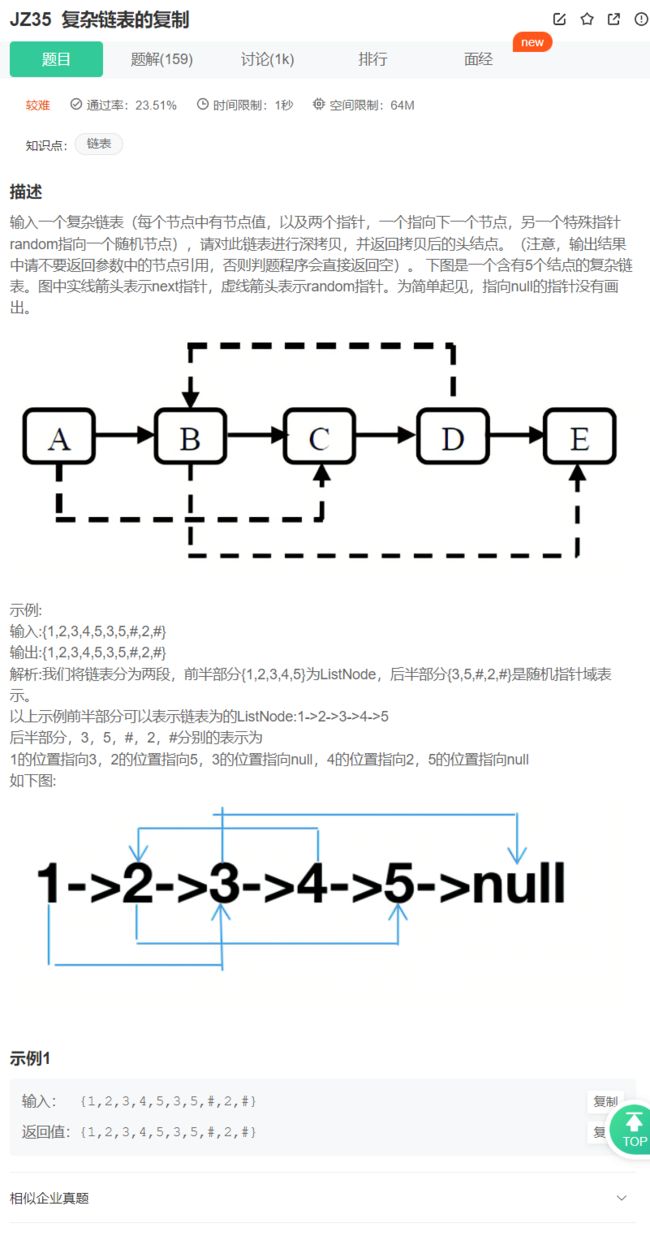
25.复杂链表的复制
刚一上眼,嚯,困难,是我能做的么?然后抱着心态试了试,想简单了,还是有很多地方没有注意到
class Solution { // 错误思路
public:
RandomListNode* Clone(RandomListNode* pHead) {
if (!pHead) return nullptr;
RandomListNode* root = new RandomListNode(pHead->label);
RandomListNode* tmp = pHead;
while (tmp) {
root->next = new RandomListNode(tmp->next->label);
if (tmp->random) {
root->random = new RandomListNode(tmp->random->label);
} else {
root->random = nullptr;
}
root = root->next;
tmp = tmp->next;
}
return root;
}
};
还是看大神的题解吧,这种哈希做法,很赞
class Solution {
public:
RandomListNode* Clone(RandomListNode* pHead) {
if (!pHead) return nullptr;
unordered_map<RandomListNode* , RandomListNode*> umap;
for (auto p = pHead; p != nullptr; p = p->next) {
umap[p] = new RandomListNode(p->label);
}
for (auto p = pHead; p != nullptr; p = p->next) {
umap[p]->next = umap[p->next];
umap[p]->random = umap[p->random];
}
return umap[pHead];
}
};
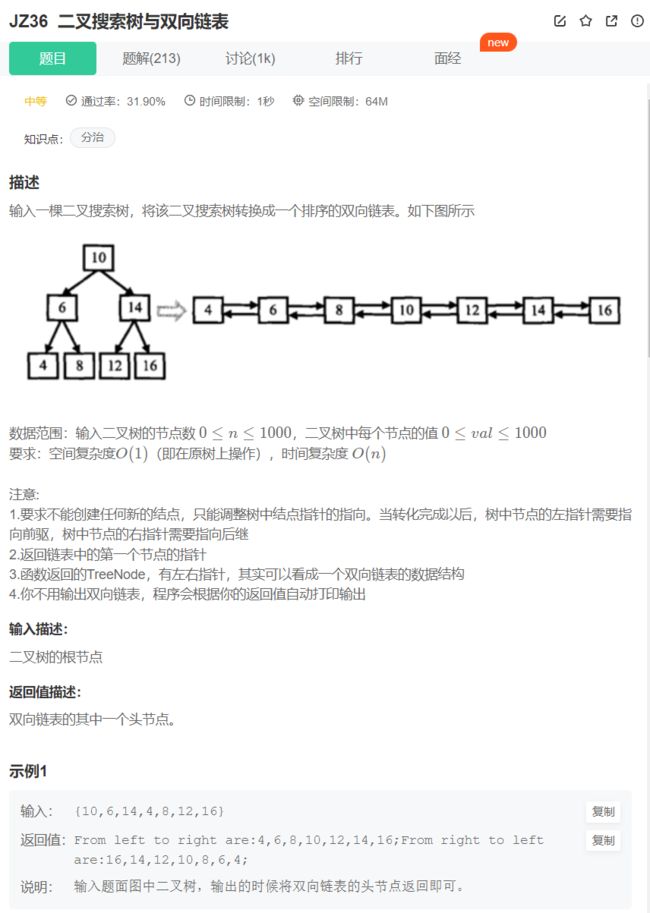
26.二叉搜索树与双向链表
中序遍历二叉树,存放在数组中,然后修改指针指向
class Solution {
public:
TreeNode* Convert(TreeNode* pRootOfTree) {
if (!pRootOfTree) return pRootOfTree;
vector<TreeNode*> result;
LDR(pRootOfTree, result);
for (int i = 0; i < result.size() - 1; i++) {
result[i]->right = result[i + 1];
result[i + 1]->left = result[i];
}
return result[0];
}
void LDR(TreeNode* root, vector<TreeNode*>& result) {
if (!root) return;
if (root->left) {
LDR(root->left, result);
}
result.push_back(root);
if (root->right) {
LDR(root->right, result);
}
}
};
思路与前面一样,先中序遍历到数组中,再改变指向
class Solution {
public:
TreeNode* Convert(TreeNode* pRootOfTree) {
if (!pRootOfTree) return pRootOfTree;
vector<TreeNode*> result;
stack<TreeNode*> sk;
// 利用栈形成中序遍历添加到数组中
while(!sk.empty() || pRootOfTree) {
if (pRootOfTree) {
sk.push(pRootOfTree);
pRootOfTree = pRootOfTree->left;
} else {
pRootOfTree = sk.top();
sk.pop();
result.push_back(pRootOfTree);
pRootOfTree = pRootOfTree->right;
}
}
// 修改链表指针指向。
for (int i = 0; i < result.size() - 1; ++i) {
result[i + 1]->left = result[i];
result[i]->right = result[i+1];
}
return result[0];
}
};
利用栈来进行原地修改,这种很好
class Solution {
public:
TreeNode* Convert(TreeNode* pRootOfTree) {
if (!pRootOfTree) return pRootOfTree;
TreeNode* head = nullptr; // 输出
TreeNode* pre = nullptr; // 记录上一次的出栈值
stack<TreeNode*> sk;
while(!sk.empty() || pRootOfTree) {
while (pRootOfTree) {
sk.push(pRootOfTree);
pRootOfTree = pRootOfTree->left;
}
if (!sk.empty()) {
pRootOfTree = sk.top();
sk.pop();
if (pre != nullptr) {
pre->right = pRootOfTree;
pRootOfTree->left = pre;
} else { // pre 为空,表示sk第一次出栈,第一次出栈值为最左值,即输出值
head = pRootOfTree;
}
pre = pRootOfTree;
pRootOfTree = pRootOfTree->right;
}
}
return head;
}
};
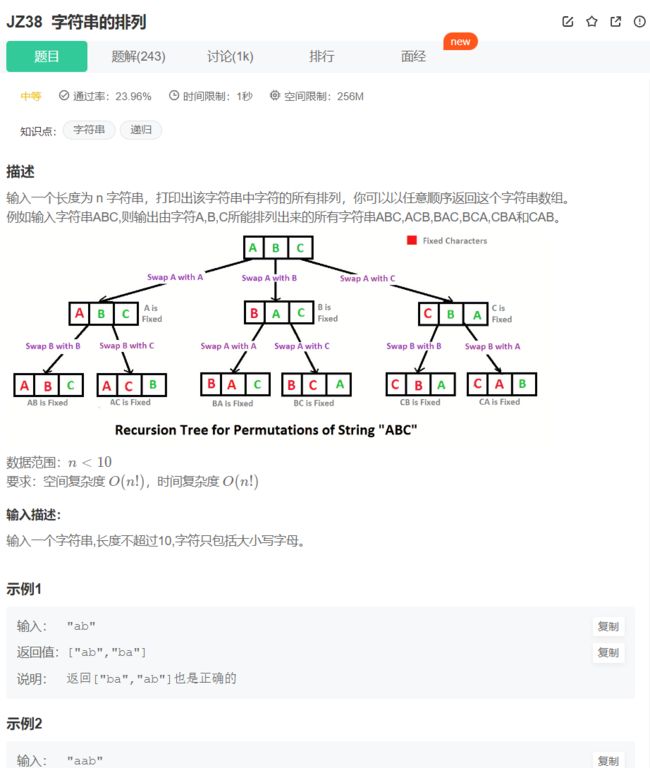
27.字符串的排列
class Solution {
public:
vector<string> Permutation(string str) {
if (0 == str.size()) return vector<string>();
vector<string> res;
sort(str.begin(), str.end());
do {
res.push_back(str);
} while (next_permutation(str.begin(), str.end()));
// next_permutation()是按字典顺序,求当前排列的下一个排列,所以要先排序
return res;
}
};
思路是递归,将字符串分为两部分,第一个字符和后面的字符,通过DFS+回溯,
(1) 遍历出所有可能出现在第一个位置的字符(依次将第一个字符同后面所有字符交换);
(2) 固定第一个字符,求后面字符的排列
这样就实现了将大问题划分为小问题
class Solution {
public:
vector<string> res;
void DFS(string& s, vector<string>& res, int begin) {
if (begin == s.size()) {
res.push_back(s);
return;
}
unordered_map<int, int> visited;
for (int i = begin; i < s.size(); i++) {
if (visited[s[i]] == 1) continue;
swap(s[i], s[begin]);
DFS(s, res, begin + 1);
swap(s[i], s[begin]);
visited[s[i]] = 1;
}
}
vector<string> Permutation(string str) {
if (str.empty()) return res;
sort(str.begin(), str.end());
DFS(str, res, 0);
return res;
}
};
28.数组中出现次数超过一半的数字
哈希做法,很常规
class Solution {
public:
int MoreThanHalfNum_Solution(vector<int> numbers) {
unordered_map<int, int> umap(0);
int len = numbers.size();
for (int i = 0; i < len; i++) {
umap[numbers[i]]++;
if (umap[numbers[i]] > len / 2) return numbers[i];
}
return 0;
}
};
摩尔投票法
思路是,数组中有一个数字出现的次数超过数组长度的一半
那么它出现的次数比其他数字出现次数的和还要多,最后次数不为0的数字即为所求
class Solution {
public:
int MoreThanHalfNum_Solution(vector<int> numbers) {
int num = numbers[0]; // 从第一个数字开始
int times = 1; // 目前出现次数为 1
for (int i = 1; i < numbers.size(); i++) {
if (0 == times) { // 为0,说明当前数字出现的次数小于其他数字出现的次数和,不满足
num = numbers[i]; // 再比较新的数字出现次数
times = 1;
} else {
num == numbers[i] ? times++ : times--; // 比较,相等+1,不相等-1
}
}
return num; // 返回最后times不为0的num,即出现次数最多的num
}
};
29.最小的K个数
第一眼,看到,就想到这样写,然后就AC了,
class Solution {
public:
vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {
sort(input.begin(), input.end());
return vector<int>(input.begin(), input.begin() + k);
}
};
接着看了眼题解,好么,大佬的做法就是不一样,基本上都是排序,快排,堆排;不过,排序还是要会的…
快排,quickSort()的作用不是排序整个数组,而是搜索并返回最小的 k 个数。
class Solution {
public:
vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {
if (k >= input.size()) return input;
return quickSort(input, k, 0, input.size() - 1);
}
vector<int> quickSort(vector<int>& input, int k, int left, int right) {
int i = left, j = right;
while (i < j) { // 哨兵划分为左右子数组
while (i < j && input[j] >= input[left]) j--;
while (i < j && input[i] <= input[left]) i++;
swap(input[i], input[j]);
}
swap(input[i], input[left]);
// 如果i < k,说明第 k + 1小的数字在右子数组中,则递归右子数组
if (i < k) quickSort(input, k, i + 1, right);
// 如果i > k,说明第k + 1小的数字在左子数组中,则递归左子数组
if (i > k) quickSort(input, k, left, i - 1);
// 如果k == i,说明此时arr[k]即为第k + 1小的数字,则直接返回数组前k个数字即可
vector<int> res;
res.assign(input.begin(), input.begin() + k);
return res;
}
};
通过优先队列,内置了堆排序
class Solution {
public:
vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {
if (k >= input.size()) return input;
// 升序队列,这里是小顶堆
priority_queue<int, vector<int>, greater<int>> pq;
for (auto num : input) {
pq.push(num);
}
vector<int> res;
while (k--) {
res.push_back(pq.top());
pq.pop();
}
return res;
}
};
30.连续子数组的最大和
总的来说就是dp,
dp数组的含义就是,当前位置出现的连续子数组和
初态,dp[0] = array[0]
状态改变,dp[i] = max(array[i], dp[i - 1] + array[i])
class Solution {
public:
int FindGreatestSumOfSubArray(vector<int> array) {
int len = array.size();
vector<int> dp(len, 0);
dp[0] = array[0];
int maxNum = array[0];
for (int i = 1; i <len; i++) {
dp[i] = max(array[i], dp[i - 1] + array[i]);
maxNum = max(maxNum, dp[i]);
}
return maxNum;
}
};
可以对空间进行优化
class Solution {
public:
int FindGreatestSumOfSubArray(vector<int> array) {
int maxNum = array[0];
for (int i = 1; i < array.size(); i++) {
array[i] = max(0, array[i - 1]) + array[i];
maxNum = max(maxNum, array[i]);
}
return maxNum;
}
};
31.整数中1出现的次数
class Solution {
public:
int NumberOf1Between1AndN_Solution(int n) {
if (n <= 0) return 0;
if (n < 10) return 1;
int high = n, pow = 1;
while (high >= 10) { // 取出 最高位,最高位对应的权重
high /= 10;
pow *= 10;
}
int last = n - high * pow; // 取出除最高位剩余部分
int cnt = high == 1 ? last + 1 : pow;
return cnt + high * NumberOf1Between1AndN_Solution(pow - 1) + NumberOf1Between1AndN_Solution(last);
}
};
32.把数组排成最小的数
若 a+b < b + a 则 a 排在 b 前
如 2 21 因为 212 < 221 所以 排序后为 21 2
to_string() 可以将int 转化为string
class Solution {
public:
string PrintMinNumber(vector<int> numbers) {
vector<string> tmp;
for (auto i : numbers) {
// 将一个左值强制转化为右值引用
tmp.push_back(std::move(to_string(i)));
}
sort(tmp.begin(), tmp.end(), [](const string& a, const string& b) {return a + b < b + a; });
string ans;
for (auto s : tmp) {
ans += std::move(s);
}
return ans;
}
};
33.丑数
根据丑数特性,只能被2, 3, 5整除,所以一个丑数可以由另一个丑数乘以2, 3, 5得到,
从1开始,依次找到后面最小的丑数,加入容器中
class Solution {
public:
int GetUglyNumber_Solution(int index) {
if (index < 7) return index;
vector<int> res(index, 0);
res[0] = 1; // 1为丑数
int indexTwo = 0, indexThree = 0, indexFive = 0;
for (int i = 1; i < index; i++) {
// 找到下一个最小的丑数
int minNum = (min(res[indexTwo] * 2, res[indexThree] * 3), res[indexFive] * 5);
if (minNum == res[indexTwo] * 2) indexTwo++;
if (minNum == res[indexThree] * 3) indexThree++;
if (minNum == res[indexFive] * 5) indexFive++;
res[i] = minNum;
}
return res[index - 1];
}
};
34.第一个只出现一次的字符
class Solution {
public:
int FirstNotRepeatingChar(string str) {
unordered_map<char, int> umap;
for (int i = 0; i < str.size(); i++) {
umap[str[i]]++;
}
for (int i = 0; i < str.size(); i++) {
if (umap[str[i]] == 1) return i;
}
return -1;
}
};
35.数组中的逆序对
class Solution {
public:
int mergeSort(vector<int>& data, vector<int>& tmp, int start, int end) {
if (start >= end) return 0;
int mid = start + (end - start) / 2;
int res = mergeSort(data, tmp, start, mid) + mergeSort(data, tmp, mid + 1, end);
int low1 = start, high1 = mid;
int low2 = mid + 1, high2 = end;
int tmpIndex = low1;
while (low1 <= high1 && low2 <= high2) {
if (data[low1] <= data[low2]) {
tmp[tmpIndex++] = data[low1++];
} else {
tmp[tmpIndex++] = data[low2++];
res += high1 - low1 + 1;
res %= 1000000007;
}
}
while (low1 <= high1) {
tmp[tmpIndex++] = data[low1++];
}
while (low2 <= high2) {
tmp[tmpIndex++] = data[low2++];
}
copy(tmp.begin() + start, tmp.begin() + end + 1, data.begin() + start);
return res % 1000000007;
}
int InversePairs(vector<int> data) {
if (data.size() == 0) return 0;
vector<int> tmp(data.size());
return mergeSort(data, tmp, 0, data.size() - 1);
}
};
36.两个链表的第一个公共结点
两根指针,走相同的路程(pHead1 + pHead2),会同时到达终点
也就是说,这两根指针最后会同时到达第一个公共的结点,然后一起到达终点
class Solution {
public:
ListNode* FindFirstCommonNode( ListNode* pHead1, ListNode* pHead2) {
ListNode* p1 = pHead1;
ListNode* p2 = pHead2;
while (p1 != p2) {
p1 = (p1 == nullptr ? pHead2 : p1->next);
p2 = (p2 == nullptr ? pHead1 : p2->next);
}
return p1;
}
};
37.数字在升序数组中出现的次数
二分,当查找到目标数组后,向前后扩展搜索
class Solution {
public:
int GetNumberOfK(vector<int> data ,int k) {
if (0 == data.size()) return 0;
int low = 0, high = data.size() - 1;
while (low <= high) {
int mid = low + (high - low) / 2;
if (data[mid] > k) high = mid - 1;
else if (data[mid] < k) low = mid + 1;
else {
int cnt = 1;
int index = mid - 1;
while (index >= 0 && data[index] == k) {
cnt++;
index--;
}
index = mid + 1;
while (index <= data.size() - 1 && data[index] == k) {
cnt++;
index++;
}
return cnt;
}
}
return 0;
}
};
38.二叉树的深度
迭代版本
class Solution {
public:
int TreeDepth(TreeNode* pRoot) {
if (!pRoot) return 0;
queue<pair<TreeNode*, int>> q;
q.push(make_pair(pRoot, 1));
int maxDepth = 1;
while (!q.empty()) {
TreeNode* curNode = q.front().first;
int curDepth = q.front().second;
q.pop();
if (curNode) {
maxDepth = max(maxDepth, curDepth);
q.push({curNode->left, curDepth + 1});
q.push({curNode->right, curDepth + 1});
}
}
return maxDepth;
}
};
递归版本
class Solution {
public:
int TreeDepth(TreeNode* pRoot) {
if (!pRoot) return 0;
int leftDepth = TreeDepth(pRoot->left);
int rightDepth = TreeDepth(pRoot->right);
return 1 + max(leftDepth, rightDepth);
}
};
39.判断是不是平衡二叉树
自顶向下
class Solution {
public:
int getDepth(TreeNode * node){
if(node == nullptr) return 0;
return 1 + max(getDepth(node->left), getDepth(node->right));
}
bool IsBalanced_Solution(TreeNode* pRoot) {
if(pRoot == nullptr) return true;
return abs(getDepth(pRoot->left) - getDepth(pRoot->right)) <= 1 &&
IsBalanced_Solution(pRoot->left) && IsBalanced_Solution(pRoot->right);
}
};
上面做法,出现个问题就是会重复遍历
自底向上
class Solution {
public:
int getDepth(TreeNode* node) {
if (!node) return 0;
int leftDepth = getDepth(node->left);
if (leftDepth == -1) return -1;
int rightDepth = getDepth(node->right);
if (rightDepth == -1) return -1;
if (abs(leftDepth - rightDepth) > 1) {
return -1;
} else {
return 1 + max(leftDepth, rightDepth);
}
}
bool IsBalanced_Solution(TreeNode* pRoot) {
if (!pRoot) return true;
return getDepth(pRoot) != -1;
}
};
40.数组中只出现一次的数字
使用异或,根据异或特性,两个相同的值异或值为0,0异或任何数值为其本身
思路是,
通过异或,将数组中成对的值都抵消,求出两个不相同数的异或的值
从右边找到第一个1的位的位置,可以根据这个位,将数组分为两个子数 组,这样就将两个不同的值分开
然后再分别异或两个子数组求出两个值
class Solution {
public:
bool isBit_1(int num, int sign) {
num >>= sign;
return (num & 1);
}
void FindNumsAppearOnce(vector<int> data,int* num1,int *num2) {
int num = 0;
// 找到不同的两个数字异或的值
for (int i = 0; i < data.size(); i++) {
num ^= data[i];
}
// 从右边找到第一个1的位的位置
int sign = 0;
while ((num & 1) == 0 && sign < 32) {
num >>= 1;
sign++;
}
*num1 = 0, *num2 = 0;
for (int i = 0; i < data.size(); i++) {
if (isBit_1(data[i], sign)) { // 分组,为1的一组,为0的一组
*num1 ^= data[i];
} else {
*num2 ^= data[i];
}
}
}
};