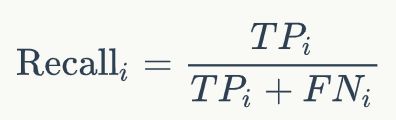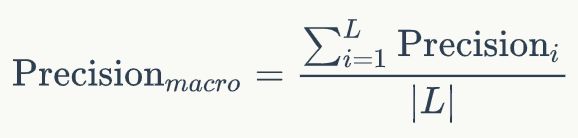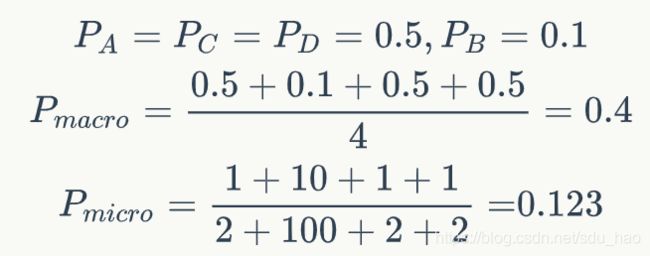深度学习 | (5) 2分类、多分类问题评价指标以及在sklearn中的使用

目录

1. 二分类评价指标

2. 多分类评价指标

3. 总结

---

1. 二分类评价指标

常用的二分类评价指标包括准确率、精确率、召回率、F1-score、AUC、ROC、P-R曲线、MCC等

• 混淆矩阵

2分类问题的混淆矩阵是2*2的，通常以关注的类为正类，另一个类为负类，分类器在数据集上的预测或者正确或者不正确，我们有4种情况：

1）TP:True Positive，实际为正类并预测为正类

2）FP：False Positve，实际为负类但预测为正类

3）TN：True Negative，实际为负类并预测为负类

4）FN：False Negative，实际为正类但预测为负类

第一个字母表示分类正确与否， T 表示分类正确， F表示分类错误； 第二个字母表示分类器判定结果， P表示判定为正例， N表示判定为负例。

2分类混淆矩阵表示如下：

• 准确率（Accuracy）

评价分类问题的性能指标一般是分类准确率，即对于给定的数据，分类正确的样本数占总样本数的比例。

注意：准确率这一指标在Unbalanced数据集上的表现很差，因为如果我们的正负样本数目差别很大，比如正样本100个，负样本9900个，那么直接把所有的样本都预测为负， 准确率为99%，但是此分类模型实际性能是非常差的，因为它把所有正样本都分错了。

• 精确率（Precision）

精确率是指在预测为正类的样本中真正类所占的比例。即预测为正类的样本中，真正为正类的样本占多少。

• 查全率(召回率，Recall)

召回率是指在真实为正类的样本中被预测为正类的比例。即真实为正类的样本中，预测为正类的样本占多少。

• F1-score

精确率高，意味着分类器要尽量在 “更有把握” 的情况下才将样本预测为正样本， 这意味着精确率能够很好的体现模型对于负样本的区分能力，精确率越高，则模型对负样本区分能力越强。如，假币预测，就需要很高的精确率，我需要你给我的预测数据具有很高的准确性。

召回率高，意味着分类器尽可能将所有有可能为正样本的样本预测为正样本，这意味着召回率能够很好的体现模型对于正样本的区分能力，召回率越高，则模型对正样本的区分能力越强。如，肿瘤预测，需要很高的召回率，“宁可错杀三千，不可放过一个”。

F1-Score: 精确率和召回率的调和平均(2/F1 = 1/P + 1/R)。 即：

因为Precision和Recall是一对相互矛盾的量，当P高时，R往往相对较低，当R高时， P往往相对较低，所以为了更好的评价分类器的性能，一般使用F1-Score作为评价标准来衡量分类器的综合性能。

而更一般的有 F_beta:

其实，  Beta本质上是Recall， Precision 权重比， 当 Beta=2时，  F2表明 Recall 的权重要比Precision高，Recall影响更大 （更侧重于Recall）； 当Beta=0.5时，  F0.5表明Recall 的权重要比Precision低， 对应的影响更小（更侧重于Precision）.

• MCC

MCC 主要用于衡量二分类问题，其综合考虑了 TP TN, FP , FN， 是一个比较均衡的指标， 对于样本不均衡情况下也可以使用。MCC的取值范围在 [-1, 1]， 取值为1 表示预测与实际完全一致， 取值为0表示预测的结果还不如随机预测的结果， -1 表示预测结果与实际的结果完全不一致。因此我们看到， MCC 本质上描述了预测结果与实际结果之间的相关系数。

值得注意的是，对于两个2分类器而言，可能其中一个分类器的 F1 值较高，而其 MCC 值较低， 这表示单一的指标是无法衡量分类器的所有优点与缺点的。

• ROC

TPR：True Positive Rate，真正率， TPR代表能将正例分对的概率（真实为正类的所有样本中，预测为正类的占多少/Recall）

FPR: False Positive Rate， 假正率， FPR代表将负例错分为正例的概率（真实为负类的所有样本中，预测（错分）为正类的占多少）

使用FPR作为横坐标，TPR作为纵坐标得到ROC曲线如下：

ROC曲线中的四个点和一条线：

1）(0,1):FN=0,FP=0(错分为负类或正类的样本数都为0)，表示所有样本都正确分类，这是一个完美的分类器；

2）(1,0):TN=0,TP=0(正确分类为负类或正类的样本数都为0)，表示所有样本都分类错误，这是一个最糟糕的分类器；

3）(0,0):FP=0,TP=0(错分、正确分类为正类的样本数都为0)，表示所有样本都分类为负；

4）(1,1):TN=0,FN=0(正确分类、错分为负类的样本数都为0)，表示所有样本都分类为正；

5）上图虚线 y = x，该对角线实际上表示一个随机猜测的分类器的结果。

经过以上分析，ROC曲线越靠近左上角，该分类器的性能越好。（多个2分类器，每个2分类器都会有一个ROC曲线，选择ROC曲线靠近左上角的2分类器）。

ROC曲线画法：在二分类问题中，测试/验证部分通常是获得一个概率表示当前样本属于正例的概率， 我们往往会采取一个阈值，大于该阈值的为正例， 小于该阈值的为负例。 当该阈值为0时，也就是把所有样本预测为正类，此时FPR、TPR=1最大； 当该阈值为1时，也就是把所有样本预测为负类，此时FPR、TPR=0最小；当增大阈值时，预测为正类（正确预测为正类）和错分为正类的样本都减少，即TP、FP都减小，FPR、TPR减小。每次选取一个不同的threshold，就可以得到一组FPR和TPR,即ROC曲线上的一点（选取的阈值越多，ROC曲线越平滑）。

 

• AUC

很多时候， ROC 曲线并不能清晰的说明哪个分类器的效果更好， 而 AUC 恰恰能够对分类器做出直观的评价。AUC 为ROC 曲线下的面积， 这个面积的数值介于0到1之间， 能够直观的评价出分类器的好坏， AUC的值越大， 分类器效果越好（ROC曲线越接近左上角）。

1）AUC=1: 完美分类器， 采用该模型，不管设定什么阈值都能得出完美预测（绝大多数时候不存在）

2）0.5

3）AUC=0.5（y=x下的面积）： 跟随机猜测一样，模型没有预测价值。

4）AUC<0.5:比随机猜测还差，但是如果反着预测，就优于随机猜测。

值得一提的是，两个模型(两个2分类器)的AUC 相等并不代表模型的效果相同， 比如这样：

• P-R曲线

P-R 曲线其横坐标为 Recall， 纵坐标为 Precision， 其能帮助我们很好的做出权衡。

 在上图中，我们发现， A 完全包住了C， 着意味着A 的Precision 与 Recall 都高于C， A优于C。 而对比 A,B， 二者存在交叉的情况，此时采用曲线下面积大小衡量性能，面积越大，性能越好，此处的A优于B。

P-R曲线于ROC曲线的对比：

ROC曲线特性：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡（class imbalance）现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化。）

下图是ROC曲线和Precision-Recall曲线的对比：

a,c为ROC曲线，b,d为P-R曲线；a,b 为在原始测试集(balanced)上的结果（两个2分类器的ROC曲线和P-R曲线），c,d为把原始数据集的负样本增加10倍后的结果。很明显，ROC曲线基本保持不变，P-R曲线变化较大。 

为什么取AUC较好？因为一个二分类问题，如果你取P或R的话，那么你的评价结果和你阈值的选取关系很大，但是我这个一个分类器定了，我希望评价指标是和你取得阈值无关的，也就是需要做与阈值无关的处理。所以AUC较P-R好。

所以对于2分类问题，我们一般采用AUC（ROC曲线下的面积）作为评价指标。

• sklearn中的使用

from sklearn.metrics import confusion_matrix,classification_report,accuracy_score,precision_score,recall_score,f1_score,roc_auc_score
#Y_test1,Y_pred1分别是表示标签和预测结果的整数索引 
Y_test1 = np.array([0,1]).repeat([8,12]) #假设标签为0的样本8个 为1的样本12个
Y_pred1 = np.array([0,1]).repeat(10) #生成20个预测结果
np.random.seed(3)  #随机打乱 label和预测结果
np.random.shuffle(Y_test1)
np.random.shuffle(Y_pred1)
print(Y_test1)
print(Y_pred1)
#生成混淆矩阵 混淆矩阵的第一个值cm1[0][0]表示实际为0类，预测为0类的样本数，cm1[1][0]表示实际为1类，预测为0类的样本数。
#其他类似
cm1 = confusion_matrix(Y_test1,Y_pred1)
print(cm1)
#分类报告第一行 以标签0为正类 标签1为负类的情况下（此时cm[0][0]代表TP），计算presion、recall、f1
#分类报告第二行 以标签1为正类 标签0为负类的情况下（此时cm[1][1]代表TP），计算presion、recall、f1
print(classification_report(Y_test1, Y_pred1,target_names=["政治","体育"],digits=2))#假设标签0代表政治、标签1代表体育  digits可以设置小数点后保留的位数 默认是2
print(accuracy_score(Y_test1,Y_pred1))#2分类多分类都可以用  
#normalize参数默认为True计算准确率 ，normalize参数为False时，计算正确分类的样本数
print(accuracy_score(Y_test1,Y_pred1,normalize=False))

#以下指标默认情况下针对2分类(可以添加labels参数，改为多分类，之后会用到) 
#各个指标的计算默认是以标签1为正类(pos_label参数=1) 标签0为负类的情况计算的（此时cm[1][1]代表TP）对应分类报告第2行
print("--------------")
print(precision_score(Y_test1,Y_pred1))
print(recall_score(Y_test1,Y_pred1))
print(f1_score(Y_test1,Y_pred1))

print("------------------")
#修改pos_label=0 各个指标的计算以标签0为正类 1为负类 对应分类报告第1行
print(precision_score(Y_test1,Y_pred1,pos_label=0))
print(recall_score(Y_test1,Y_pred1,pos_label=0))
print(f1_score(Y_test1,Y_pred1,pos_label=0))

print("-------------------")
#计算各个指标的宏平均、微平均、加权平均
print(f1_score(Y_test1,Y_pred1,average='micro'))
print(f1_score(Y_test1,Y_pred1,average='macro'))
print(f1_score(Y_test1,Y_pred1,labels=[0,1],average='weighted'))

print(precision_score(Y_test1,Y_pred1,average='micro'))
print(precision_score(Y_test1,Y_pred1,average='macro'))
print(precision_score(Y_test1,Y_pred1,labels=[0,1],average='weighted'))
print("------------------")
#auc
print(roc_auc_score(Y_test1,Y_pred1))

2. 多分类评价指标

评价多分类问题时，通常把多分类问题分解成多个2分类问题。即n分类，分解为n个2分类，每次以其中一个类为正类，其余类统一为负类，计算之前提到的各种2分类指标，最后再平均计算多分类评价指标，有三种平均方式，之后会介绍。

分别计算第i类的Precision、Recall和F1-score（把第i类当作正类，其余所有类统一为负类）：

 

 

• Macro 宏平均

分别计算第i类的Precision、Recall和F1-score（把第i类当作正类，其余所有类统一为负类），然后进行平均（假设总共有L个类）：

那么我们就得到最终的 Macro F1 的计算为：

我们看到， Macro F1 本质上是所有类别的统计指标的算术平均值来求得的，这样单纯的平均忽略了样本之间分布可能存在极大不平衡的情况。

• Micro ：微平均

Micro 算法在计算 Precision 与 Recall 时会将所有类直接放到一起来计算。

• macro vs. micro

Macro 相对 Micro 而言，小类别起到的作用更大，举个例子而言，对于一个四分类问题有：

 那么对于 Precision 的计算有：

我们看到，对于 Macro 来说， 小类别相当程度上拉高了 Precision 的值，而实际上， 并没有那么多样本被正确分类，考虑到实际的环境中，真实样本分布和训练样本分布相同的情况下，这种指标明显是有问题的， 小类别起到的作用太大，以至于大样本的分类情况不佳。 而对于 Micro 来说，其考虑到了这种样本不均衡的问题， 因此在这种情况下相对较佳。

总的来说， 如果你的类别比较均衡，则随便； 如果你认为大样本的类别应该占据更重要的位置， 使用Micro； 如果你认为小样本也应该占据重要的位置，则使用 Macro； 如果 Micro << Macro ， 则意味着在大样本类别(样本数比较多的类)中出现了严重的分类错误； 如果 Macro << Micro ， 则意味着小样本类别中出现了严重的分类错误。

为了解决 Macro 无法衡量样本均衡问题，一个很好的方法是求加权的 Macro， 因此 Weighed F1 出现了。

• weight加权平均

Weighted 算法算术 Macro 算法的改良版，是为了解决Macro中没有考虑样本不均衡的原因， 在计算 Precision与Recall 时候，各个类别的 Precision 与 Recall要乘以该类在总样本中的占比来求和：

那么我们就得到最终的 Macro F1 的计算为：

•  ROC和AUC

在多分类场景下，比如C分类，ROC曲线应该有多个(每次以其中一个类为正类，其余类为负类)，多分类AUC的计算如下：

•  sklearn中的使用

多分类，以三分类为例：

from sklearn.metrics import confusion_matrix,classification_report,accuracy_score,precision_score,recall_score,f1_score,roc_auc_score
#Y_test2,Y_pred2分别是表示标签和预测结果的整数索引 
Y_test2 = np.array([0,1,2]).repeat([8,12,10]) #假设标签为0的样本8个 为1的样本12个,为2的样本10个
Y_pred2 = np.array([0,1,2]).repeat(10) #生成30个预测结果
np.random.seed(3)  #随机打乱 label和预测结果
np.random.shuffle(Y_test2)
np.random.shuffle(Y_pred2)
print(Y_test2)
print(Y_pred2)
#生成混淆矩阵 混淆矩阵的第一个值cm2[0][0]表示实际为0类，预测为0类的样本数，cm2[1][0]表示实际为1类，预测为0类的样本数。cm2[2][2]表示实际为2类，预测为2类的样本数
#其他类似
cm2 = confusion_matrix(Y_test2,Y_pred2)
print(cm2) #三分类情况下 混淆矩阵3*3
#分类报告第一行 以标签0为正类 其余类（标签1，2）为负类的情况下（此时cm[0][0]代表TP），计算presion、recall、f1
#分类报告第二行 以标签1为正类 其余类（标签0，2）为负类的情况下（此时cm[1][1]代表TP），计算presion、recall、f1
#分类报告第三行 以标签2为正类 其余类（标签0，1）为负类的情况下（此时cm[2][2]代表TP），计算presion、recall、f1
#下面是多分类的三种平均指标
#第i类的Precision= cm[i][i]/sum(cm[:][i]) 
#第i类的Recall= cm[i][i]/sum(cm[i][:]) 
#第i类的F1-score通过 第i类的Precision和Recall进行计算
#micro 微平均 的Precision、Recall、F1-score都相等 也等于分类准确率 其值就是混淆矩阵对角线元素之和比上混淆矩阵所有元素和
print(classification_report(Y_test2, Y_pred2,target_names=["政治","体育","财经"],digits=2))#假设标签0代表政治、标签1代表体育、标签2代表财经 digits可以设置小数点后保留的位数 默认是2

print("----------------")
#准确率 正确分类的样本数 比上 总样本数
print(accuracy_score(Y_test2,Y_pred2)) #混淆矩阵对角线元素之和 比上 混淆矩阵所有元素和
#正确分类的样本数
print(accuracy_score(Y_test2,Y_pred2,normalize=False))
print("-------------------")

#计算各个指标的宏平均、微平均、加权平均
#不传labels参数也可以 会自动识别各个label
print(f1_score(Y_test2,Y_pred2,average='micro'))
print(f1_score(Y_test2,Y_pred2,average='macro'))
print(f1_score(Y_test2,Y_pred2,labels=[0,1,2],average='weighted'))

print(recall_score(Y_test2,Y_pred2,average='micro'))
print(recall_score(Y_test2,Y_pred2,average='macro'))
print(recall_score(Y_test2,Y_pred2,labels=[0,1,2],average='weighted'))

3. 总结

对于最终分类指标的选择， 在不同数据集，不同场景，不同时间下都会有不同的选择，但往往最好选出一个指标来做优化，对于二分类问题，我目前用 AUC 比较多一些， 多分类我还是看 F1 值（micro、macro、weighted）。