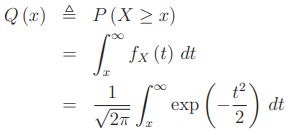通信原理复习笔记（EEEN3005J Communication Theory）(8)
目录
前言
Chapter 12 Random Signals
12.1 随机变量（Random Variables，RVs）
12.1.1 离散随机变量（Discrete Random Variables）
12.1.2 连续随机变量（Continuous Random Variables）
12.1.2.1 概率密度函数（PDF）
12.1.2.2 累积分布函数（CDF）
12.1.2.3 CDF和PDF之间的关系
12.1.3 预期（Expectation）
12.1.3.1 函数的预期值
12.1.3.2 矩（moment）
12.1.3.3 中心矩（和方差）（Central moments (and variance)）
12.1.3.4 高斯分布（Gaussian distribution）
12.1.3.5 归一化高斯函数和Q函数（Normalized Gaussian, and the Q function）
这种关系如图12.1.2所示。
12.1.3.6 中心极限定理（Central limit theorem）
12.2 平稳随机过程（Stationary Random Processes）
12.2.1 自相关函数（Auto-correlation function）
12.2.1.1 激励示例（Motivational example）
12.2.2 广义平稳（WSS）随机过程（Wide Sense Stationary (WSS) Random Processes）
12.2.3 遍历随机过程 （Ergodic Random Processes）
前言
本笔记是基于北京都柏林学院2022年EEEN3005J Communication Theory课程课件总结出的笔记。任课教师为Dr Deepu John。
阳老板建议: 本节内容之后的为期末考试内容，前11章内容配合期末试卷一同使用效果最佳。
Chapter 12 Random Signals
12.1 随机变量（Random Variables，RVs）
随机变量X是一个与实验结果有关的数字。如果我们重复实验，我们可能会得到一个不同的数字，以一种不可预测的方式——每次重复实验都会产生一个样本值。
12.1.1 离散随机变量（Discrete Random Variables）
离散随机变量是指只能从有限的一组可能值中取值的变量，示例包括：
• 掷骰子
• 从牌堆中挑选一张牌
• 轮盘赌的价值。
我们通过其概率质量函数（PMF）
来描述离散随机变量，定义如下：
pmf告诉我们每个可能结果的概率。例子：
• 扔骰子：
• 从牌堆中挑选一张牌：
• 轮盘赌：
注意所有概率之和=1。
这是因为，当然，可以保证（即概率=1）每次都会发生一个结果。我们可以用数学来表达：
其中的总和是x的所有可能值。
12.1.2 连续随机变量（Continuous Random Variables）
连续随机变量可以在连续范围内取任意值，
例如
• 随机选择的人的身高。
• 噪声电阻器上的电压振幅
让我们进一步看看第一个例子，并提出以下问题：
1.随机选择的人身高1.7米的概率是多少？
2.随机选择的人身高2.7米的概率是多少？
在北京（2010年），人的平均身高是1.747米，所以我们可能认为
170万人的概率远远高于270万人，对吗？也许不是。如果…怎么办
我们将问题重新表述如下：
1.随机选择的人身高1.70000000’米的概率是多少？
2.随机选择的人身高2.70000000’米的概率是多少？
（这里的’意味着永远重复）。
我们没有改变这个问题，但现在答案是什么？
0 ！！！！
我们可以把它放在数学中，对于一个连续的随机变量来说
因此，对于x的每一个可能值，连续RV的PMF为零；
PMF是连续RVs概率的无用度量，我们需要另一个工具。。。
12.1.2.1 概率密度函数（PDF）
基于以上讨论，讨论X在一系列值上的概率才有意义。因此，我们定义了概率密度函数（PDF），它具有以下性质：
其在[a，b]范围内的积分（或从x=a到b的曲线下的面积）给出了x在该范围内（包括）获得一个值的概率。
现在我们可以问以下问题：
1.随机选择的人身高在1.69到1.71米之间的概率是多少？
2.随机选择的人身高在2.69到2.71米之间的概率是多少？
现在，这些问题将有非零答案，如图12.1.1所示。
PDF具有以下性质
• 该函数为非负函数，
• 该函数总和为1，
12.1.2.2 累积分布函数（CDF）
有时（实际上通常）更容易考虑RV小于（或等于）某个值的概率，因此我们将连续随机变量X的累积分布函数（CDF）定义为：
一些属性：
• 它包含与PDF相同的所有信息
• 这是一个非递减函数
12.1.2.3 CDF和PDF之间的关系
从CDF的定义来看：
其中
是
的PDF。
这也可以写为：
从这两个表达式可以清楚地看出，或
足以完全描述独立RV，因为我们可以使用它们来计算任何结果的概率。
根据它们，我们可以计算RV函数的值，以及一些重要的基本统计数据，例如均值和方差。
12.1.3 预期（Expectation）
问：如果你多次重复一个实验，平均结果值是多少？
A. 把它们加起来，除以实验次数。
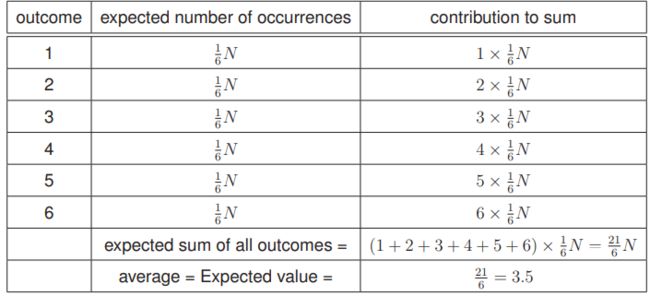
让我们考虑一下掷骰子N次的离散示例。我们预计会得到
次的“一”和次的“二”
等等。把这些放在一张桌子上，我们有：
您可以在Matlab中轻松证明这一点：
我们可以概括地说，离散RV的预期值（或平均值，或真实平均值）为：
其中，求和是对x的所有可能值进行的，是的PMF。
通过这种极限情况，可以证明，对于连续变量，我们有以下期望值：
其中现在是RV的PDF。
期望值代表了“真实”的平均值，考虑了所有可能（无限多）的结果及其概率。它与样本平均数
′相反，是N（有限个）样本值的平均值：
我们当然愿意相信
，在这种情况下，我们可以说X'是平均值的无偏估计。
12.1.3.1 函数的预期值
对于任何函数
，
的期望，随机变量的函数，是
从这一点很容易看出预期是线性的，即:
因此，期望函数是线性的：
12.1.3.2 矩（moment）
X的n阶矩被定义为
例：n=1；![E[X^1] =m_x](http://img.e-com-net.com/image/info8/4060c96ca3254874a08f8a3dc16b8250.gif){kind=small}
是X的平均值。
例：n=2；![E[X^2]](http://img.e-com-net.com/image/info8/090f2091e11d47f4ac5fd4a936c924c7.gif){kind=small}
是X的均方值。X的均方值指示X的“大”程度。
12.1.3.3 中心矩（和方差）（Central moments (and variance)）
X的第n阶中心矩为：
例： n=2; 
为X的方差
X的方差给我们提供了X关于其平均值的变化程度的指示。
方差具有以下属性：
方差的平方根σX称为X的标准偏差。
注意：
12.1.3.4 高斯分布（Gaussian distribution）
示例：高斯分布随机变量（也称为正态分布随机变量）由PDF描述：
注意，这个分布只有两个参数，即
和
。
练习：表明该RV的均值和方差确实是和。
基于此，可以说变量是高斯分布的，具有特定的均值和方差，我们通常使用简写符号：
∼ 在概率论中经常被用来表示RV是如何分布的（它并不意味着“等于”）
12.1.3.5 归一化高斯函数和Q函数（Normalized Gaussian, and the Q function）
归一化高斯随机变量的
，方差
，即
。
其PDF格式如下：
归一化高斯PDF尾部下的区域在通信理论中经常使用，我们给它起了一个特殊的名字，Q函数：
数学家们喜欢的互补误差函数是由
这些都与以下公式有关：
这种关系如图12.1.2所示。
正如我们稍后将看到的，所谓的“Q函数”
在分析数字通信系统的性能时是有用的。
12.1.3.6 中心极限定理（Central limit theorem）
中心极限定理（这里没有证明）说，如果你把足够的独立和相同的分布加在一起。
RVs结果具有高斯分布，与原始分布无关，事实上：
这就是为什么我们发现高斯RVs无处不在——电子工程也不例外，
在大型电路中，有许多独立的噪声源，可以（小心地）将它们集中到一个高斯分布中，从而大大降低分析的复杂性。
12.1.4 相关随机变量（Correlated RVs）
到目前为止，我们只考虑了独立的随机变量，即结果独立于其他任何东西的随机变量。在考虑随机过程之前，我们先简单介绍一下
相关随机变量。考虑图12.1.3中的电路。
显然，我们有：
然而，他们并不独立。
我们的意思是，如果我们知道其中一个，那么我们就知道另一个，在这种情况下，我们知道关于另一个的一切；我们说这两个RVs是相关的。
我们通过相关系数
测量两个随机变量 X和Y之间的相关性，定义为：
练习：对于我们的分压器电路
。
总的来说，我们有：
• ρ = 0 ⇒变量是独立的
• 0 < ρ < 1 ⇒这些变量在某种程度上是相关的，也就是说，知道其中一个可以告诉我们关于另一个的一些事情（但不是全部）。
• ρ = 1 ⇒变量是100%相关的，也就是说，知道其中一个可以告诉我们关于另一个的一切。
12.2 平稳随机过程（Stationary Random Processes）
随机过程，或随机过程，是指产生输出
的过程，
是时间的函数，只能用统计方法描述，示例包括：
•自动抛硬币的机器——这是一个离散的随机过程，因为可能的值是“正面”或“反面”。
•每单位时间到达一家商店的客户数量——这是一个离散的随机过程，因为可能的值为1、2、3······，等等。这通常由一个“到达率”参数建模。
•电阻器；通过它的电压总是包含一个随时间变化的随机分量——噪声通常是零均值高斯分布
理论上，所有这些示例过程本身都是时变的，即它们的统计数据随时间而变化，即:
• 投币机运行多年后，其统计数据将与其原始设置不同
• 我们预计，与白天相比，夜间顾客到达商店的速度会有所不同。
• 电阻器上的噪声随着温度的变化而变化，因此可能会在一天和一年中发生变化。
因此，这些都是非平稳随机过程的例子。
然而非平稳随机过程很难处理——因此在工程中，我们通常假设这些过程在分析的时间跨度内是平稳的。我们将不再考虑非平稳过程！
平稳随机过程的统计参数不随时间变化。
1.通信信道中的噪声是一个随机过程——描述这个过程可以让我们计算出信道噪声对通信系统性能的影响
2.完成后，我们可以进一步设计通信系统（发射器和接收器），以尽量减少这种影响。
3.从接收器的角度来看，信息信号也可以被视为一个随机过程。如果接收器知道信息信号，就不需要通信。因此，还需要对信息信号进行统计表征。
假设X是一个平稳的随机过程，有一个输出，那么我们可以将其视为一个随机变量——与前一节课中的随机变量没有什么不同，只是我们需要包含t，所以我们使用稍微不同的表示法：它的CDF是：
及其PDF格式：
例如，一个非常常见的过程称为高斯过程，
对所有t具有高斯分布：
X的平均值为：
这是一个常数（随着时间的推移），因为我们假设这是一个平稳的过程。
12.2.1 自相关函数（Auto-correlation function）
因此，除了上述一些定义中的t参数外，平稳随机过程的各个方面与正则独立随机变量没有区别，
PDF和CDF允许在不参考任何其他时间
的情况下，描述某个时间
到的输出的统计信息。为了检验随机过程的输出是如何随时间变化的，我们需要一些额外的统计工具。
12.2.1.1 激励示例（Motivational example）
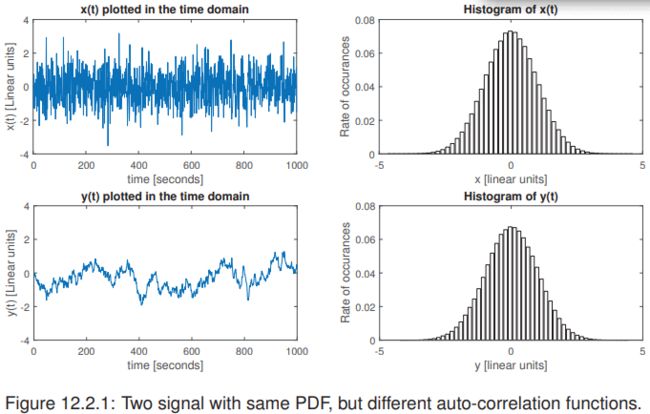
考虑图12.2.1所示的两个信号和
。这些都是在Matlab中生成的。
我们注意到了什么？
根据直方图，它们似乎都是高斯分布的——这是正确的，事实上它们都是高斯分布
但很明显，它们在时域上“看起来”非常不同——这怎么可能呢？
我知道（因为我生成了它们），的每个样本都是独立的，但是的样本不是独立的，它们是相互关联的。如果我知道
，那么我知道关于
的一些（但不是全部），我们可以说它们有一个自相关系数
.
当然，这取决于具体的时间实例t1和t2，所以我们定义
的自相关函数为
这与自相关系数的定义不同，因为没有非劣化因子。
这测量了在两个不同时间t1、t2的两个过程样本之间的相关性。
12.2.2 广义平稳（WSS）随机过程（Wide Sense Stationary (WSS) Random Processes）
如果一个随机过程的所有统计量都不随时间变化，那么它就是严格意义上的平稳过程。广义平稳性是一个较为宽松但被广泛使用的定义。如果仅满足以下两个条件，则随机过程为广义平稳（WSS）：
• 平均值与时间无关，即：
• 自相关函数仅取决于样本之间的时间差（导致以下滥用符号）：
其中
是时间差。这里的要点是，自相关函数仅取决于此时间偏移，即t1和t2之间的时间，而不取决于t1或t2。
12.2.3 遍历随机过程 （Ergodic Random Processes）
在长度为
的区间内，平稳随机过程输出的时间平均值如下所示：
如果
也就是 
, 那么X的平均值是遍历的。
在长度为的区间内，平稳随机过程输出的自相关如下所示：
如果
也就是 , 那么X在自相关函数中是遍历的
遍历性对于一个随机过程来说是一个很好的特性，因为它意味着我们可以通过替换测量的时间平均值来估计“真实”平均值和自相关，并且这些估计随着
还要注意，遍历过程必须是平稳的，但平稳过程不一定是遍历的。
我们将假设所有随机过程都是WSS，并且在均值和自相关中是遍历的。