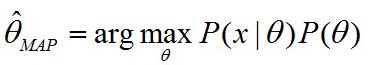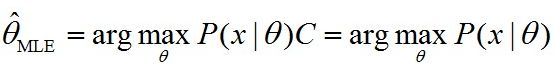- 读书笔记06‖《时间管理,如何充分利用你的24小时》
Gemini_565d
54分钟,你没有听错,我读完了这本妙趣横生的书!总共128页,平均每分钟2页的阅读速度,我能行,你可以做到!作者用幽默诙谐的语言向我们讲述了时间管理的有效方法,字数不多,风格独特,没有废话!实际上并不单单指你24小时的内容!且来看看这本不占用你时间,但给你提出时间管理的技巧!01.主要结构与内容1.篇章结构上半部分:如何利用时间?下半部分:是否正在使用时间发挥最大效用?2.主要概念(1)意识是时间
- 506:缴费29年,50岁退休,养老金有增发有过渡,到手多少?
社保小龙虾
社保知识,小龙虾每日分享第506期,欢迎关注!“我表姑,1972年出生,正好50周岁退休,缴纳社保有29年,这个养老金是不是算错了?”有网友表示,29年的社保缴纳,退休后养老金却没有2000元,是不是算错了。下面一起看看具体是如何计算的。一、基本信息1972年出生,2022年退休,退休年龄50岁,计发基数195个月;缴费年限29年,其中实际缴费年限26.92年,视同缴费年限2.08年;当地市级计发
- 通过Netplan为Ubuntu服务器新增DNS以解析内部域名
在企业网络环境中,Ubuntu服务器常常需要访问内部服务,这些服务通常通过内部域名进行寻址。如果服务器默认配置的DNS无法解析这些内部域名,就需要手动添加公司的内部DNS服务器地址。本章节将详细介绍如何在Ubuntu22.04LTS服务器上使用Netplan工具新增DNS服务器IP,并提供解决配置后可能遇到的常见问题的步骤,确保服务器能够顺利解析内部域名。前提条件拥有一台运行Ubuntu22.04
- 时间才是最大的财富
杭州财富流沙盘俱乐部
上周去杭州师范大学,和几个大二的同学组织了一场财富流游戏。游戏结束后,我的第一感觉就是:年轻真好!我们大部分人参加财富流游戏是为了反思和总结,而他们是用来规划和展望。因为他们处于游戏中的起点:20岁的年龄。真的很羡慕他们在最美好的年龄就能接触投资理财方面的知识,给他们以启迪和思考,能够提早规划以后的人生和投资理财思路。整个沙盘推演过程,也让我对这帮00后的孩子有了新的认识,首先他们做事很认真,整个
- 体验身体感觉
sanmaopipi
头脑里的画面是对自己所见所闻的投射,当头脑把投射的记忆画面翻出来之后进行加工,通过声音评价评判记忆画面,产生身体感觉,有时候让大脑发紧,有时候肚子里产生一定的气体,鼓鼓的紧紧的不舒服,有时候对当下的抗拒对事实的反抗,更加让自己生出起来,身体产生紧或者张的感觉,进而让自己失去对当下的觉知,对身体感觉的感知,进而让自己失去对自己的觉知,当回归后感觉不太好。
- 触摸心灵的温度
一笑一尘缘2019
大雁跨越天际,留下拍动羽翼的身影;白云漫步蓝天,留下潇洒的痕迹;你来过我的世界,留下触摸心灵的温度。二十岁那年,临近暑假。离开父母转眼又是半年,相处时恨不得离他们远远的,离开后尽是思念。考完最后一科,已是下午四点多。那时的交通没现在这么发达,过了四点已经没有回家的车了。可又很想去车站碰碰运气,万一有一辆迟归的车呢。奇迹这种事总时时会发生的!年轻的心就这么偏执。我到车站,华灯渐已次第绽放,车站似乎冷
- 渴望
爱丽丝成长日记
大部分人的真正差异不在于他们的智商水平,而在于他们的活力,这生活中的种活力来源于哪里呢?有人说,一种强烈和迫切的渴望,一个明确的目的,一个不可动摇的决心,可以让我们达成几乎任何事情。这个就是普通人和伟人之间的最大区别。你的渴望是什么呢?你内心的渴望是什么??当我们讨伦内心渴望时,我们需要讨论人生的一些方面,要花一些时间,严肃认识的思考。探讨我是谁,我的人生究竟为了什么?我要这个世界上实现什么?等等
- 《重生复仇:渣男你别想逃》《南初筝、南辰桡》完整版免费全文在线赏析_《重生复仇:渣男你别想逃》最新章节无广告
霸道推书2
小说简介:前世,我掉进了渣男的陷阱里面,被他吃得骨头渣子都不剩,重生后,我回到了关键的时间节点,这一次,我不会再抗拒养兄对我的爱了,毕竟前世他的一切举动,证明了他对我的爱。这一世,我要凭着前世记忆大斗渣男,手撕无良亲生父母,我要把养兄捧在掌心,许他一世深情。书名:《重生复仇:渣男你别想逃》主角配角:南初筝、南辰桡推荐指数:✩✩✩✩✩———小说内容试读———楚净月哭哭啼啼的回到昭勇侯府,楚侯爷不在家
- 孕期日记|不同的胎动 美好的春光
天边的星
孕26周2天,今日宝宝,366mm,860g。小宝宝的个头又变大了,活动也更加频繁。以前感觉肚子在动,我就把手放在肚子上,感受宝宝的活动。最近,我感受到宝宝的活动后,就把衣服掀开,仰坐在沙发上,看肚子的动静。常常都是掀开衣服宝宝就不动了,过一会儿才又开始动。这一次,感觉到宝宝在动之后,我又赶紧掀开衣服看。没想到宝宝还挺给面子,我看到肚子居然有起伏,而且很明显。以前也见到过肚子的起伏,但是那是上下如
- 笔趣阁&《八年烬空》小说TXT莫莞妍凌致远完本小说阅读,太是那个了~#八年烬空
今日推文2
书名:《八年烬空》主角:莫莞妍凌致远阅读建议:↓想看后续的小伙伴请打开微信公众号-【花儿文库】关注并回复数字:281,即可开始阅读~慢条斯理走到莫沫熙跟前,我一边同她说话,一边抄起那碗她最喜欢的西式浓汤,不紧不慢的,往她头上倒去。事情发生的不算多么突然,只是谁都没有意料到,在莫家,一向唯唯诺诺的大女婿,会做出这种极度不合礼数的举动。大概有好几秒的时间,老宅安静的过于诡异。直到莫沫熙后知后觉的发出刺
- #转# 在新月和满月不练习Ashtanga瑜伽,为什么?
图书管理员阿紫
因为在新月和满月的日子里,太阳和月亮对地球引力最大,如海水的潮汐现象等。我们跟所有含水物质一样,会受到月亮盈亏的影响(人体重量约有60%--70%成份是液体[水的元素])。月圆月缺由月亮跟太阳的相对位置决定,月亮和太阳相对时为满月,会合时为新月。新月的时候太阳月亮在同一侧,我们可以看到它黑暗的背阳面;满月时,太阳在西和月亮在东,它们由太阳相隔遥遥相对,我们可以看到整个月亮的向阳面.在这两天当中,太
- 妻妾成群
小灰象
颂莲被抬进陈家花园做四太太的那一年她十九岁,大学一年级没读完。家里茶厂的倒闭伴着父亲的死和她的辍学。继母给她两条路,做工或嫁人。她说,当然是嫁人。嫁穷人还是有钱人。当然是有钱人,她说。做小也是好的。颂莲嫁进陈家的那天去见大太太,在佛堂诵经的大太太得知后没有抬头看她,随后扯断了手中的佛珠。口中念念有词,罪过,罪过。颂莲的住处在后花园的南厢房里,紧挨着三太太梅珊的住处。早听说三太太有倾国倾城之貌,颂莲
- Python基础(字符串的切片与断言)
日暮凡尘
python开发语言pycharm
'''1.输入一个字符串,判断是否只包含英文字母(大写或小写)。输出True或False。2.输入一个字符串,统计里面数字字符(0-9)的数量。3.输入两个字符串,第一个是主串,第二个是要查找的字符,判断字符是否在主串中。4.输入一个字符串,将所有数字字符转换成整数后求和。5.统计字符串中空格的数量6.输入字符串和数字n,判断字符串是否只包含数字且长度等于n。7.验证用户输入的手机号格式(中国手机
- 蔬菜排骨汤
爱做早餐的小娜子
蔬菜排骨汤爱做早餐的小娜子娜家便当6天前温馨提示:你们的关注、阅读以及点赞,是对我最大的鼓励。因为当天的早晨做不到当天分享,都需要延迟一天才能分享,所以这次调整一下。每周一至周五更新哦。工作日早餐分享:主食:花卷汤:蔬菜排骨汤小菜:凉拌芦笋丝水果:丑桔准备食材:食材A:排骨、胡萝卜、藕、玉米、小葱、葱、姜食材B:普通面粉350g、发酵粉4g、小葱食材C:丑桔、芦笋蔬菜排骨汤:排骨清洗后,放入冷水锅
- C语言:数组-字符串数组
数组字符串基础操作在用格式化说明符%s进行输入输出时,其输入输出项均为数组名。但在输入时,相邻两个字符串之间要用空格分隔,系统将自动在字符串后加\0。在输出时,遇到结束符\0作为输出结束标志。对于字符串的操作,我们需要使用到一些系统提供的API函数。字符串输入scanf语法:scanf("%s",数组名);注意:数组名对应的数组只能是char类型,从控制台输入字符串之后,默认为追加\0案例:#in
- next.js刷新页面时二级菜单展开状态判断
啃火龙果的兔子
开发DEMOjavascript前端react.js
在Next.js中保持二级菜单刷新后展开状态的解决方案在Next.js应用中,当页面刷新时保持二级菜单的展开状态,可以通过以下几种方法实现:方法1:使用URL参数保存状态(推荐)import{useRouter}from'next/router';import{useEffect,useState}from'react';constMenuComponent=()=>{constrouter=us
- 重生后,打脸渣男贱女张晚苏蔓蔓(完整版小说)全集免费阅读重生后,打脸渣男贱女张晚苏蔓蔓~全集已完结
兔子爱阅读
重生后,打脸渣男贱女张晚苏蔓蔓(完整版小说)全集免费阅读重生后,打脸渣男贱女张晚苏蔓蔓~全集已完结主角:张晚苏蔓蔓简介:彻底摆烂后,我决定休学旅游。我退出了全国绘画比赛,有人却比我更急。男友的白月光拼命联系我,想让我重新拿起画笔。此刻的我早已在千里之外赶海浮潜,玩得不亦乐乎。上一世,我苦心创作出来的作品却被人举报抄袭。大量的证据公布出来,网上直接骂疯。解释无效,网暴升级为人身攻击,极端网友往我家丢
- 【Nacos无压力源码领读】(二) 集成 LoadBalancer 与 OpenFeign
Dexu7
SpringCloud负载均衡ribbon
上一篇文章中,详细介绍了Nacos注册中心的原理,相信看完后,大家应该完全掌握了Nacos客户端是如何自动进行服务注册的,以及Nacos客户端是如何订阅服务实例信息的,以及Nacos服务器是如何处理客户端的注册和订阅请求的;本文承上启下,在订阅服务实例的基础上,介绍如何在实例之间进行选择,实现负载均衡;并详细介绍了负载均衡组件LocaBanlancer和函数式调用组件OpenFeign是如何与Na
- LinkedHashMap/HashMap(数҉据҉缓҉存҉准҉备҉)
顾名思义LinkedHashMap是比HashMap多了一个链表的结构。与HashMap相比LinkedHashMap维护的是一个具有双重链表的HashMap,LinkedHashMap支持2中排序一种是插入排序,一种是使用排序,最近使用的会移至尾部例如M1M2M3M4,使用M3后为M1M2M4M3了,LinkedHashMap输出时其元素是有顺序的,而HashMap输出时是随机的,如果Map映射
- 宝宝经常吐奶?教你正确冲奶方法助宝宝易消化
硬核大叔
吐奶是初生宝宝成长的必经阶段,成因是婴儿胃部容量小,加上食道与胃部之间幽门肌肉仍未完全成长,所以饱餐后容易出现倒流情况,随着宝宝消化系统发展成熟,吐奶问题就会逐步消失;假如婴儿吐奶次数过于频繁或呕吐量多,有可能是冲奶手法及喂哺方式不当所致,影响宝宝消化及吸收。想让宝宝易消化,留意日常冲奶及喂哺习惯,有助减缓吐奶问题。十大贴士助宝宝减少吐奶宝宝吐奶问题加剧,容易因为不适而烦躁哭闹、胃口下降甚至体重减
- HCL 三层知识总结
HCL三层知识总结一、网络层基础1.1网络层的核心功能网络层位于数据链路层之上,主要负责跨网络的数据包转发,实现不同网段(广播域)之间的通信。其核心功能包括:寻址与路由:通过IP地址标识网络中的主机,并选择最佳路径将数据包从源端发送到目的端。分段与重组:当数据包大小超过底层链路的MTU(最大传输单元)时,将其分割为更小的片段,到达目的端后重新组合。拥塞控制:通过流量调节避免网络因过载而瘫痪(HCL
- 2022年5月10日《儿童纪律教育》培训感悟
心态决定一切
------杨丹妮+春蕾怡馨幼儿园感受:1.错误的观念小时候父母对自己的教育耳濡目染深深地留在我们的记忆里,自己有孩子后,会延续父母的教育方式。殊不知我们已经对孩子造成了伤害。我们在知道惩罚的严重性、错误性之后,通过努力改变让我们以更好的教育方式去爱我们的孩子。2、压力大现在的成人生活压力大,压力不能得到很好的宣泄,在一直压抑着自己,当孩子犯错误时压力积累控制不住发泄到孩子身上。所以不要积攒太多的
- 2018-06-28 tree 便利显示
lazyTai
image.png//rendertree.jsconstpaddingLeft={paddingLeft:10}functionrenderChildren(data,datasource,props){returnMap(data,item=>{return{renderChildren(datasource[item.key],datasource,props)}})}//rendertre
- 酒后故事(六十一)
沉葉
(六十一)阿里要兵分两路调查火拼案,赛琳娜在酒吧醋意大发前面讲到楼下门铃响起男主人开了门,是邻居过来发圣诞节请帖,约他们一起过圣诞节,老人很高兴接了请帖,并送走了邻居。赛琳娜与亚力克山这才放下心来。阿里到酒吧没有得到想要的信息,只拿到了酒吧女招待的电话,而这个电话很明显被酒吧女招待废弃了,他回到警局后,召集组里的警察开会,兵分两路一路去查酒吧亚力克山那伙人,另外一路去医院查住院这伙人。杰罗姆提前来
- 《和离后他再说爱我》凌杏宋天翊(完结篇)全文免费阅读【笔趣阁】
桃子爱阅读
《和离后他再说爱我》凌杏宋天翊(完结篇)全文免费阅读【笔趣阁】主角:凌杏宋天翊简介:成婚八年,凌杏想给宋天翊一个惊喜。听到关门声,装睡的凌杏马上唤来侍女更衣。准备了一月,她今天要亲自去接他下朝。只是来的过早了,整整等了一个时辰,才终于见到穿着朝服的官员缓步走出。“翊哥哥!你等等我。”刚满十六的少女格外娇俏,对着前方的男人言语中都带着一丝撒娇意味。凌杏一怔。随即,宋天翊的声音传来:“别急,小心脚下。
- 微信小程序分包
難釋懷
微信小程序小程序
一、前言随着微信小程序功能的不断扩展,代码体积也逐渐增大。而微信小程序对主包大小限制为2MB(压缩后),超过这个限制将无法上传发布。为了解决这一问题,小程序分包机制应运而生——它允许我们将一个大型小程序拆分为多个子包,按需加载,从而突破大小限制并提升首屏加载速度。本文将带你全面掌握:✅小程序分包的基本原理✅分包的配置方式(app.json)✅主包与子包的通信机制✅页面路径的引用规则✅分包预下载策略
- 《和老婆双双重生后,我们双双逃婚了》(刘佳高天明)最新章节免费在线阅读~我和老婆一起重生到十年前的婚礼上我们不顾父母亲友的反对,不提原因,都坚定地要取消这场婚礼分道扬镳后,她和另一个追求者火速在...
小说全集全本阅读
《和老婆双双重生后,我们双双逃婚了》(刘佳高天明)最新章节免费在线阅读~我和老婆一起重生到十年前的婚礼上我们不顾父母亲友的反对,不提原因,都坚定地要取消这场婚礼分道扬镳后,她和另一个追求者火速在一起,一同去了国外主角配角:刘佳高天明简介:4我此话一出,立马引起了轩然大波高天明都还没来得及反驳,一堆狗腿子就纷纷帮着他反驳我“秦枫你怎么这么酸啊,怎么就这么仇富呢?”“就是啊,还说人家高总的是假表,你见
- Softprep软件安装管理器v1.3.0.4装机员专用一键安装工具及教程
Softprep软件安装管理器v1.3.0.4装机员专用一键安装工具及教程【下载地址】Softprep软件安装管理器v1.3.0.4装机员专用一键安装工具及教程Softprep软件安装管理器v1.3.0.4是一款专为电脑系统装机员设计的高效工具,旨在简化重装系统后的软件安装流程。通过一键操作,用户可以快速安装常用软件,如QQ、迅雷、IDM下载器等,极大提升装机效率。支持自定义安装包,用户可根据需求
- #晓悦晨享记 282
xuxiaoyue88
一点点的专注加上长久的持续,就能事半功倍!这两天给一个基础薄弱的五年级学生补习英语课,每天放学后一个小时,刚开始一个单元10个单词,在学校学完了最多会读三四个,更不要说课文了。所以这两天主要帮她通过音标先来读记单词,这个过程中也要求她把专注力用在拼读上面,结果还是不错的,昨天晚上读和默写就达到了80%的合格率。对于孩子来说,很难意识到专注力的重要性,但是对于我们成年人来说,你的专注力在哪,结果就会
- D065+8组煎果子+《高效能人士的7个习惯》读书笔记
煎果子
习惯一:积极主动时下盛行的社会观点认为,环境与条件对我们起着决定性的作用。我们不否认条件作用的影响巨大,但并不等于承认它凌驾于一切之上,甚至可以决定我们的命运。在外界的刺激与最后的回应之间,人拥有选择的自由,这也是人与动物之间最大的不同。史蒂芬•柯维指出,看一个人的时间和精力集中于哪些事物,就可以大致判断出他是否积极主动。作者将我们关注的问题分成两类:关注圈和影响圈。关注圈,是指我们关注的问题,包
- xml解析
小猪猪08
xml
1、DOM解析的步奏
准备工作:
1.创建DocumentBuilderFactory的对象
2.创建DocumentBuilder对象
3.通过DocumentBuilder对象的parse(String fileName)方法解析xml文件
4.通过Document的getElem
- 每个开发人员都需要了解的一个SQL技巧
brotherlamp
linuxlinux视频linux教程linux自学linux资料
对于数据过滤而言CHECK约束已经算是相当不错了。然而它仍存在一些缺陷,比如说它们是应用到表上面的,但有的时候你可能希望指定一条约束,而它只在特定条件下才生效。
使用SQL标准的WITH CHECK OPTION子句就能完成这点,至少Oracle和SQL Server都实现了这个功能。下面是实现方式:
CREATE TABLE books (
id &
- Quartz——CronTrigger触发器
eksliang
quartzCronTrigger
转载请出自出处:http://eksliang.iteye.com/blog/2208295 一.概述
CronTrigger 能够提供比 SimpleTrigger 更有具体实际意义的调度方案,调度规则基于 Cron 表达式,CronTrigger 支持日历相关的重复时间间隔(比如每月第一个周一执行),而不是简单的周期时间间隔。 二.Cron表达式介绍 1)Cron表达式规则表
Quartz
- Informatica基础
18289753290
InformaticaMonitormanagerworkflowDesigner
1.
1)PowerCenter Designer:设计开发环境,定义源及目标数据结构;设计转换规则,生成ETL映射。
2)Workflow Manager:合理地实现复杂的ETL工作流,基于时间,事件的作业调度
3)Workflow Monitor:监控Workflow和Session运行情况,生成日志和报告
4)Repository Manager:
- linux下为程序创建启动和关闭的的sh文件,scrapyd为例
酷的飞上天空
scrapy
对于一些未提供service管理的程序 每次启动和关闭都要加上全部路径,想到可以做一个简单的启动和关闭控制的文件
下面以scrapy启动server为例,文件名为run.sh:
#端口号,根据此端口号确定PID
PORT=6800
#启动命令所在目录
HOME='/home/jmscra/scrapy/'
#查询出监听了PORT端口
- 人--自私与无私
永夜-极光
今天上毛概课,老师提出一个问题--人是自私的还是无私的,根源是什么?
从客观的角度来看,人有自私的行为,也有无私的
- Ubuntu安装NS-3 环境脚本
随便小屋
ubuntu
将附件下载下来之后解压,将解压后的文件ns3environment.sh复制到下载目录下(其实放在哪里都可以,就是为了和我下面的命令相统一)。输入命令:
sudo ./ns3environment.sh >>result
这样系统就自动安装ns3的环境,运行的结果在result文件中,如果提示
com
- 创业的简单感受
aijuans
创业的简单感受
2009年11月9日我进入a公司实习,2012年4月26日,我离开a公司,开始自己的创业之旅。
今天是2012年5月30日,我忽然很想谈谈自己创业一个月的感受。
当初离开边锋时,我就对自己说:“自己选择的路,就是跪着也要把他走完”,我也做好了心理准备,准备迎接一次次的困难。我这次走出来,不管成败
- 如何经营自己的独立人脉
aoyouzi
如何经营自己的独立人脉
独立人脉不是父母、亲戚的人脉,而是自己主动投入构造的人脉圈。“放长线,钓大鱼”,先行投入才能产生后续产出。 现在几乎做所有的事情都需要人脉。以银行柜员为例,需要拉储户,而其本质就是社会人脉,就是社交!很多人都说,人脉我不行,因为我爸不行、我妈不行、我姨不行、我舅不行……我谁谁谁都不行,怎么能建立人脉?我这里说的人脉,是你的独立人脉。 以一个普通的银行柜员
- JSP基础
百合不是茶
jsp注释隐式对象
1,JSP语句的声明
<%! 声明 %> 声明:这个就是提供java代码声明变量、方法等的场所。
表达式 <%= 表达式 %> 这个相当于赋值,可以在页面上显示表达式的结果,
程序代码段/小型指令 <% 程序代码片段 %>
2,JSP的注释
<!-- -->
- web.xml之session-config、mime-mapping
bijian1013
javaweb.xmlservletsession-configmime-mapping
session-config
1.定义:
<session-config>
<session-timeout>20</session-timeout>
</session-config>
2.作用:用于定义整个WEB站点session的有效期限,单位是分钟。
mime-mapping
1.定义:
<mime-m
- 互联网开放平台(1)
Bill_chen
互联网qq新浪微博百度腾讯
现在各互联网公司都推出了自己的开放平台供用户创造自己的应用,互联网的开放技术欣欣向荣,自己总结如下:
1.淘宝开放平台(TOP)
网址:http://open.taobao.com/
依赖淘宝强大的电子商务数据,将淘宝内部业务数据作为API开放出去,同时将外部ISV的应用引入进来。
目前TOP的三条主线:
TOP访问网站:open.taobao.com
ISV后台:my.open.ta
- 【MongoDB学习笔记九】MongoDB索引
bit1129
mongodb
索引
可以在任意列上建立索引
索引的构造和使用与传统关系型数据库几乎一样,适用于Oracle的索引优化技巧也适用于Mongodb
使用索引可以加快查询,但同时会降低修改,插入等的性能
内嵌文档照样可以建立使用索引
测试数据
var p1 = {
"name":"Jack",
"age&q
- JDBC常用API之外的总结
白糖_
jdbc
做JAVA的人玩JDBC肯定已经很熟练了,像DriverManager、Connection、ResultSet、Statement这些基本类大家肯定很常用啦,我不赘述那些诸如注册JDBC驱动、创建连接、获取数据集的API了,在这我介绍一些写框架时常用的API,大家共同学习吧。
ResultSetMetaData获取ResultSet对象的元数据信息
- apache VelocityEngine使用记录
bozch
VelocityEngine
VelocityEngine是一个模板引擎,能够基于模板生成指定的文件代码。
使用方法如下:
VelocityEngine engine = new VelocityEngine();// 定义模板引擎
Properties properties = new Properties();// 模板引擎属
- 编程之美-快速找出故障机器
bylijinnan
编程之美
package beautyOfCoding;
import java.util.Arrays;
public class TheLostID {
/*编程之美
假设一个机器仅存储一个标号为ID的记录,假设机器总量在10亿以下且ID是小于10亿的整数,假设每份数据保存两个备份,这样就有两个机器存储了同样的数据。
1.假设在某个时间得到一个数据文件ID的列表,是
- 关于Java中redirect与forward的区别
chenbowen00
javaservlet
在Servlet中两种实现:
forward方式:request.getRequestDispatcher(“/somePage.jsp”).forward(request, response);
redirect方式:response.sendRedirect(“/somePage.jsp”);
forward是服务器内部重定向,程序收到请求后重新定向到另一个程序,客户机并不知
- [信号与系统]人体最关键的两个信号节点
comsci
系统
如果把人体看做是一个带生物磁场的导体,那么这个导体有两个很重要的节点,第一个在头部,中医的名称叫做 百汇穴, 另外一个节点在腰部,中医的名称叫做 命门
如果要保护自己的脑部磁场不受到外界有害信号的攻击,最简单的
- oracle 存储过程执行权限
daizj
oracle存储过程权限执行者调用者
在数据库系统中存储过程是必不可少的利器,存储过程是预先编译好的为实现一个复杂功能的一段Sql语句集合。它的优点我就不多说了,说一下我碰到的问题吧。我在项目开发的过程中需要用存储过程来实现一个功能,其中涉及到判断一张表是否已经建立,没有建立就由存储过程来建立这张表。
CREATE OR REPLACE PROCEDURE TestProc
IS
fla
- 为mysql数据库建立索引
dengkane
mysql性能索引
前些时候,一位颇高级的程序员居然问我什么叫做索引,令我感到十分的惊奇,我想这绝不会是沧海一粟,因为有成千上万的开发者(可能大部分是使用MySQL的)都没有受过有关数据库的正规培训,尽管他们都为客户做过一些开发,但却对如何为数据库建立适当的索引所知较少,因此我起了写一篇相关文章的念头。 最普通的情况,是为出现在where子句的字段建一个索引。为方便讲述,我们先建立一个如下的表。
- 学习C语言常见误区 如何看懂一个程序 如何掌握一个程序以及几个小题目示例
dcj3sjt126com
c算法
如果看懂一个程序,分三步
1、流程
2、每个语句的功能
3、试数
如何学习一些小算法的程序
尝试自己去编程解决它,大部分人都自己无法解决
如果解决不了就看答案
关键是把答案看懂,这个是要花很大的精力,也是我们学习的重点
看懂之后尝试自己去修改程序,并且知道修改之后程序的不同输出结果的含义
照着答案去敲
调试错误
- centos6.3安装php5.4报错
dcj3sjt126com
centos6
报错内容如下:
Resolving Dependencies
--> Running transaction check
---> Package php54w.x86_64 0:5.4.38-1.w6 will be installed
--> Processing Dependency: php54w-common(x86-64) = 5.4.38-1.w6 for
- JSONP请求
flyer0126
jsonp
使用jsonp不能发起POST请求。
It is not possible to make a JSONP POST request.
JSONP works by creating a <script> tag that executes Javascript from a different domain; it is not pos
- Spring Security(03)——核心类简介
234390216
Authentication
核心类简介
目录
1.1 Authentication
1.2 SecurityContextHolder
1.3 AuthenticationManager和AuthenticationProvider
1.3.1 &nb
- 在CentOS上部署JAVA服务
java--hhf
javajdkcentosJava服务
本文将介绍如何在CentOS上运行Java Web服务,其中将包括如何搭建JAVA运行环境、如何开启端口号、如何使得服务在命令执行窗口关闭后依旧运行
第一步:卸载旧Linux自带的JDK
①查看本机JDK版本
java -version
结果如下
java version "1.6.0"
- oracle、sqlserver、mysql常用函数对比[to_char、to_number、to_date]
ldzyz007
oraclemysqlSQL Server
oracle &n
- 记Protocol Oriented Programming in Swift of WWDC 2015
ningandjin
protocolWWDC 2015Swift2.0
其实最先朋友让我就这个题目写篇文章的时候,我是拒绝的,因为觉得苹果就是在炒冷饭, 把已经流行了数十年的OOP中的“面向接口编程”还拿来讲,看完整个Session之后呢,虽然还是觉得在炒冷饭,但是毕竟还是加了蛋的,有些东西还是值得说说的。
通常谈到面向接口编程,其主要作用是把系统��设计和具体实现分离开,让系统的每个部分都可以在不影响别的部分的情况下,改变自身的具体实现。接口的设计就反映了系统
- 搭建 CentOS 6 服务器(15) - Keepalived、HAProxy、LVS
rensanning
keepalived
(一)Keepalived
(1)安装
# cd /usr/local/src
# wget http://www.keepalived.org/software/keepalived-1.2.15.tar.gz
# tar zxvf keepalived-1.2.15.tar.gz
# cd keepalived-1.2.15
# ./configure
# make &a
- ORACLE数据库SCN和时间的互相转换
tomcat_oracle
oraclesql
SCN(System Change Number 简称 SCN)是当Oracle数据库更新后,由DBMS自动维护去累积递增的一个数字,可以理解成ORACLE数据库的时间戳,从ORACLE 10G开始,提供了函数可以实现SCN和时间进行相互转换;
用途:在进行数据库的还原和利用数据库的闪回功能时,进行SCN和时间的转换就变的非常必要了;
操作方法: 1、通过dbms_f
- Spring MVC 方法注解拦截器
xp9802
spring mvc
应用场景,在方法级别对本次调用进行鉴权,如api接口中有个用户唯一标示accessToken,对于有accessToken的每次请求可以在方法加一个拦截器,获得本次请求的用户,存放到request或者session域。
python中,之前在python flask中可以使用装饰器来对方法进行预处理,进行权限处理
先看一个实例,使用@access_required拦截:
?
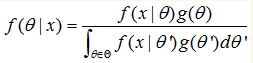

![]() 为f(x),是固定值)
为f(x),是固定值)