数值分析第一次作业-牛顿迭代法求解二元非线性方程组
1、问题
求解如下方程组:
2、算法
 3、代码实现
3、代码实现
# *coding:utf-8 *
import math
delta = 5e-6 ;eps = 1e-6
x0 = 1;y0 = 1
er = 1;k = 0
def z(x,y):
return math.sin(x*y)*math.exp(-0.1*(x**2+y**2+x*y+2*x))
def f(x,y):
return y*math.cos(x*y)-0.1*(2*x+y+2)*math.sin(x*y)
def g(x,y):
return x*math.cos(x*y)-0.1*(2*y+x)*math.sin(x*y)
def f_x(x,y):
return -y**2*math.sin(x*y)-0.2*math.sin(x*y)-0.1*(2*x*y+y**2+2*y)* math.cos(x*y)
def f_y(x,y):
return math.cos(x*y)-x*y*math.sin(x*y)-0.1*math.sin(x*y)-0.1*(2*x**2+x* y+2*x)*math.cos(x*y)
def g_x(x,y):
return math.cos(x*y)-x*y*math.sin(x*y)-0.1*math.sin(x*y)-0.1*(2*y**2+x*y)*math.cos(x*y)
def g_y(x,y):
return -x**2*math.sin(x*y)-0.2*math.sin(x*y)-0.1*(2*x*y+x**2)* math.cos(x*y)
print('使用初值为(',"{0:.1f}".format(x0),', ',"{0:.1f}".format(y0),')')
while er > 0.000000001:
x1=x0+(f(x0,y0)*g_y(x0,y0)-g(x0,y0)*f_y(x0,y0))/(g_x(x0,y0)*f_y(x0,y0) -f_x(x0,y0)*g_y(x0,y0))
y1=y0+(g(x0,y0)*f_x(x0,y0)-f(x0,y0)*g_x(x0,y0))/(g_x(x0,y0)*f_y(x0,y0) -f_x(x0,y0)*g_y(x0,y0))
er=max(abs(x1-x0),abs(y1-y0))
x0=x1;y0=y1
k=k+1
print('迭代次数',"{0:.0f}".format(k),',方程根的近似值为x=', "{0:.10f}".format(x1),',y =',"{0:.10f}".format(y1))
print('误差er=',"{0:.16f}".format(er))
print('方程组的根为(',"{0:.10f}".format(x1),',',"{0:.10f}".format(y1),')', "原函数极小值z=","{0:.10f}".format(z(x1, y1)))
当初值为(1,1)时,计算结果如表1。
 此时可以得到原二元函数的极小值点为(0.9097471401,1.3180997683),极小值为0.5330808683。然而,当初值取(-1,-1)时,可以得到原二元函数的极小值点为(-1.5221370100,-0.8914954107),极小值为0.8474932827。为什么两个结果不一样呢?
此时可以得到原二元函数的极小值点为(0.9097471401,1.3180997683),极小值为0.5330808683。然而,当初值取(-1,-1)时,可以得到原二元函数的极小值点为(-1.5221370100,-0.8914954107),极小值为0.8474932827。为什么两个结果不一样呢?
4、解决问题
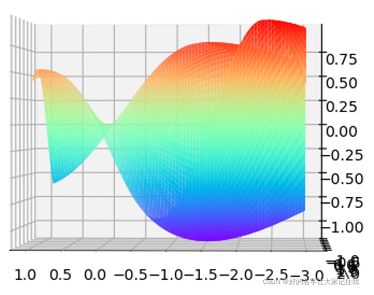
当初值不同时,得到的结果完全不一样,之所以出现这样的结果的原因是因为二元函数可能存在多个极小值点或者鞍点。为了探究原二元函数的三维空间形状,用python画出原二元函数的三维图像如图1,三维图像绘制代码picture_3D.py见附录。
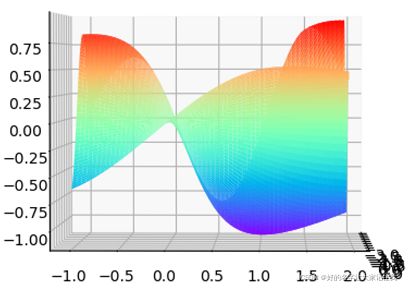
根据图1,可以清晰地看到原二元函数有且只有一个极小值点。旋转矢量图可以看出原二元函数的极小值点大约在x=-1.5,y=1处,极小值大约为-1.1,如图2、图3。。
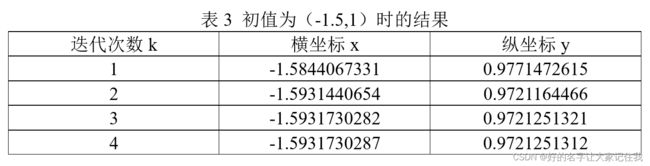
于是重新取初值为(-1.5,1),并计算结果,如表3。此时可以得到原二元函数的极小值点为(-1.5931730287,0.9721251312),极小值为-1.1330866542。
附录
# *coding:utf-8 *
import numpy as np
from matplotlib import pyplot as plt
# 定义坐标轴
fig = plt.figure()
ax1 = plt.axes(projection='3d')
# 定义三维数据
xx = np.arange(-3, 1, 0.05)
yy = np.arange(-1, 2, 0.05)
x, y = np.meshgrid(xx, yy)
z = np.sin(x * y) * np.exp(-0.1 * (x ** 2 + y ** 2 + x * y + 2 * x))
# 作图
ax1.plot_surface(x, y, z, rstride=1, cstride=1, cmap='rainbow')
ax1.contour(x, y, z, stride=0.05, zdim='z', offset=-3, cmap='rainbow') # 绘制等高线
plt.show()