「PyTorch自然语言处理系列」3. 神经网络的基本组件（中）

来源 |  Natural Language Processing with PyTorch

作者 | Rao，McMahan

译者 | Liangchu

校对 | gongyouliu

编辑 | auroral-L

全文共5283字，预计阅读时间45分钟。

上下拉动翻看整个目录

1. 感知机：最简单的神经网络

2. 激活函数

    2.1 Sigmoid

    2.2 Tanh

    2.3 ReLU

    2.4 Softmax

3. 损失函数

    3.1 均方误差损失

    3.2 分类交叉熵损失

    3.3 二元交叉熵损失

4. 深入有监督训练

    4.1 构造玩具数据

      4.1.1 选择模型

      4.1.2 转换概率到具体类

      4.1.3 选择损失函数

      4.1.4 选择优化器

    4.2 放到一起：基于梯度的监督学习

5. 补充训练概念

    5.1 正确度量模型表现：评估度量

    5.2 正确度量模型表现：分割数据集

    5.3 知道什么时候停止训练

    5.4 找到正确的超参数

    5.5 正则化

6. 示例：分类餐馆评论的情感

    6.1 Yelp 评论数据集

    6.2 理解 PyTorch 的数据集表示

    6.3 Vocabulary，Vectorizer和DataLoader

      6.3.1 Vocabulary

      6.3.2 Vectorizer

      6.3.3 DataLoader

    6.4 感知机分类器

    6.5 训练例程

      6.5.1 设置阶段来启动训练

      6.5.2 训练循环

  6.6 评估（evaluation），推理（inference）和检查（inspection）

      6.6.1 在测试数据上评估

      6.6.2 推理和分类新的数据点

      6.6.3 检查模型权重

7. 总结

    参考资料

4. 深入有监督训练

监督学习是在给定示例标签的情况下学习如何将观察结果（observation）映射到特定目标（target）的问题。在这一节中，我们将探讨更多细节。具体来讲，我们明确地描述如何使用模型预测（prediction）和损失函数（loss function）对模型参数（parameter）进行基于梯度的优化。本节内容十分重要，因为本书的其余部分都基于此，所以即使你对监督学习有些熟悉，也最好仔细阅读本节。

回顾第一章，有监督学习需要以下内容：模型、损失函数、训练数据和优化算法。监督学习的训练数据是观察和目标对，模型从观察中计算预测，损失衡量预测相对于目标的误差。训练的目的是利用基于梯度的优化算法来调整模型的参数，使损失尽可能小。

在本节的剩余部分，我们将讨论一个经典的玩具问题（toy problem）：将二维点划分为两个类中的一个。直观上，这意味着学习一条直线（称为决策边界(decision boundary)或超平面(hyperplane)）来区分类之间的点。我们将一步步描述数据构造、选择模型、选择一个损失、建立优化算法，最后一起运行这些内容。

4.1 构造玩具数据

在机器学习中，当试图理解一个算法时，创建具有易于理解属性的人造数据是一种司空见惯的做法。本节中，我们使用人造合成数据将二维点分类为两类中的一个。为了构建数据，我们从xy平面的两个不同部分采样点，为模型创建一个易于学习的环境，示例下图（3-2）所示。模型的目标是将星星（⭐）和圆圈（⚪）分别分类为两个不同的类，我们可以从图的右侧认识到这一点，虚线上方和下方的东西分类是不同的。生成数据的代码位于本章附带的 Python notebook中名为get_toy_data()的函数中。

4.4.1 选择模型

我们在这里使用的模型是本章开头所介绍的感知器。感知器是灵活的，这是因为它允许任何大小的输入。在典型的建模情况下，输入大小是由任务和数据决定的。在这个玩具示例中，输入大小为 2，这是因为我们显式地将数据构造为二维平面。对于这个二分类问题，我们为类分别指定一个数字索引：0 和 1。映射标签⭐和⚪到类的映射是任意的——只要在数据预处理、训练、评估和测试的过程中是一致的。该模型另一个重要属性是其输出的性质。由于感知器的激活函数是一个 sigmoid函数，感知器的输出就是数据点（x）为类 1 的概率，即P(y = 1 | x)。

4.1.2 转换概率到具体类

对于二分类问题，我们可以通过利用决策边界δ将输出概率转换成两个离散类。如果预测的概率P(y = 1 | x) > δ，那么预测类是 1，其他类为0。通常，这个决策边界被设置为 0.5，但在实际运用时，你可能需要微调优化这个超参数（使用一个评估数据集），以便在分类中达到理想的精度。

4.1.3 选择损失函数

在准备好数据并选择了模型体系结构之后，在有监督的训练中还可以选择另外两个重要组件：损失函数和优化器。在模型输出为概率的情况下，最合适的损失函数家族是基于交叉熵的损失函数（cross entropy–based losses）。对于这个玩具数据示例，由于模型产生二进制结果，所以我们特别使用 BCE 损失。

4.1.4 选择优化器

在这个简化的监督训练示例中，最后要选择优化器。当模型产生预测并且损失函数衡量预测和目标之间的误差时，优化器使用错误信号更新模型的权重。最简单的形式是，有一个超参数能控制优化器的更新行为，这个超参数称为学习率（learning rate），它控制错误信号对更新权重的影响。学习速率是一个关键的超参数，你应该尝试几种不同的学习速率并比较它们的效果。学习率过高会使得参数产生较大的变化，并会影响其收敛性，而学习率过低会导致在训练过程中进展甚微（收敛太慢）。

PyTorch 库提供了几种优化器以供选择。随机梯度下降法（Stochastic gradient descent，SGD）是一种经典的选择算法，但对于比较麻烦的优化问题，SGD 存在收敛性问题，往往会导致模型较差。目前首选的替代方案是自适应优化器（adaptive optimizer），例如 Adagrad 或 Adam，它们随时间变化使用关于更新的信息。在下面的例子中，我们使用 Adam，但看看其他一些不同的优化器也是有益无害的。对于 Adam，默认的学习率是 0.001。对于学习率之类的超参数，我们总是建议首选默认值，除非你从论文中获得了选取特定值的秘诀。

示例 3-9：实例化 Adam 优化器

Input[0] 
import torch.nn as nn 
import torch.optim as optim 
 
input_dim = 2 
lr = 0.001 
 
perceptron = Perceptron(input_dim=input_dim) 
bce_loss = nn.BCELoss() 
optimizer = optim.Adam(params=perceptron.parameters(), lr=lr)

4.2 放到一起：基于梯度的监督学习

学习从计算损失开始，也就是说，模型预测离目标有多远。损失函数的梯度，继而就是参数应该改变多少的信号。每个参数的梯度表示给定参数的损失值的瞬时变化率。实际上，这意味着你可以知道每个参数对损失函数的贡献有多大。直观上来看，这是一个斜率，你可以想象每个参数都站在它自己的山上，并且想要向上或向下移动一步。基于梯度的模型训练所涉及的最简单的形式就是迭代地更新每个参数，并使用与该参数相关的损失函数的梯度。

下面看一下这个梯度步进（gradient-stepping）算法长什么样。首先，所有诸如梯度之类的簿记信息当前都存储在模型（感知器）对象中，这些簿记信息都被名为zero_grad()的函数所清除。然后，模型计算给定输入数据（x_data）的输出（y_pred）。接下来，通过比较模型输出（y_pred）和预期目标（y_target）的大小来计算损失。这正是有监督训练信号的有监督部分。PyTorch 损失对象（criterion）包含一个名为backward()的函数，它通过计算图迭代地向后传播损失，并将其梯度通知给每个参数。最后，优化器（opt）使用一个名为step()的函数指导参数如何在知道梯度的情况下更新它们的值。

整个训练数据集被划分成多个批（batch）。每个梯度步的迭代都在一批数据上完成。名为batch_size的超参数指定批次大小。由于训练数据集固定，增加批的大小就会减少批的数量。

注意

在文献中，当然也包括在本书中，术语minibatch也可以和batch互换使用，以强调每个batch都明显小于训练数据的大小。例如，训练数据可能有数百万个，而minibatch可能只有几百个。

在多个批（通常是有限大小数据集中的批量数量）之后，训练循环完成了一个周期（epoch）。周期是一个完整的训练迭代。如果每个周期的批数量与数据集中的批数量相同，那么一个周期就是对数据集的完整迭代。模型是为一定数量的周期而训练的。要训练的周期数量并不难选择，但也有一些方法可以决定何时停止，我们稍后将讨论这点。如下例（3-11）所示，有监督的训练循环是一个嵌套循环：数据集或批集合上的内循环，以及外循环，后者在固定数量的周期或其他终止条件上重复内循环。

示例 3-11：感知机和二分类的有监督训练循环

# each epoch is a complete pass over the training data 
for epoch_i in range(n_epochs): 
    # the inner loop is over the batches in the dataset 
    for batch_i in range(n_batches): 
 
        # Step 0: Get the data 
        x_data, y_target = get_toy_data(batch_size) 
 
        # Step 1: Clear the gradients 
        perceptron.zero_grad() 
 
        # Step 2: Compute the forward pass of the model 
        y_pred = perceptron(x_data, apply_sigmoid=True) 
 
        # Step 3: Compute the loss value that we wish to optimize 
        loss = bce_loss(y_pred, y_target) 
 
        # Step 4: Propagate the loss signal backward 
        loss.backward() 
 
        # Step 5: Trigger the optimizer to perform one update 
        optimizer.step()

5. 补充训练概念

基于梯度的有监督学习的核心概念很简单：定义模型、计算输出、使用损失函数计算梯度、应用优化算法使用梯度更新模型参数。然而，在训练过程中有几个重要的概念需要补充了解，我们将在本节介绍其中一些概念。

5.1 正确度量模型表现：评估度量

核心的有监督训练循环之外最重要的部分是使用模型从未训练过的数据来客观衡量表现。我们使用一个或多个评估度量（evaluation metrics）对模型进行评估。在自然语言处理中有许多种评价指标。最常见的也是我们将在本章使用的就是准确性（accuracy）。简单地说，准确性就是在训练过程中未见的数据集上预测正确的部分。

5.2 正确度量模型表现：分割数据集

请一定记住：我们最终的目标是很好地概括（generalize）数据的真实分布。这又是什么意思？假设我们能够看到无限数量的数据（“真实/不可见的分布”），那么存在一个全局的数据分布。显然我们是无法看到无限数量的数据的。相反，我们用有限的样本作为训练数据。我们观察数据在有限样本中的分布，这是真实分布的近似或不完全版本。如果一个模型不仅降低了训练数据中样本的误差，而且减少了来自不可见分布的样本的误差，那么这个模型就比另一个模型具有更好的普遍性/泛化。当模型致力于降低它在训练数据上的损失时，它可能过度拟合（overfit）并适应了那些实际上不是真实数据分布一部分的特性。

要很好地概括数据的真实分布，标准实践是：要么将数据集分割为三个随机采样的分区（称为训练集training、验证集validation和测试集testing）；要么进行k-fold交叉验证（k-fold cross validation）。前者是比较简单的一种，因为它只需要一次计算。你应该采取预防措施，确保在划分的三个数据集之间的类分布保持相同。换句话说也就是通过类标签聚合数据集，然后将每个由类标签分隔的集合随机拆分为训练集、验证集和测试集，这是一种很好的实践。一个常见的分割百分比是：70% 用于训练，15% 用于验证，15% 用于测试。不过，这不是一个死板的划分约定，你当然也可以自行划分数据集的百分比。

在某些情况下，可能存在预定义的训练集、验证集和测试集，这在用于基准测试任务的数据集中很常见。在这种情况下，重要的是只使用训练数据更新模型参数、在每个周期结束时使用验证数据测量模型效果、并在选择了所有的模型以及报告了最终结果之后只使用一次测试数据。这最后一部分是极其重要的，因为机器学习工程师越是关注测试数据集上的模型效果，他们就越倾向于选择在测试集上表现更好的模型。

使用k-fold交叉验证的模型评估与使用预定义分割的评估非常相似，但是在此之前还有一个额外的步骤：将整个数据集分割为 k 个大小相同的“fold”。保留其中一个fold用于评估，剩下的k-1个fold都用于训练。这是通过交换用于评估的fold来重复的。因为有 k 个fold，每个fold都有机会成为一个评估fold，从而产生 k 个精度值。最终被报告的准确性只是具有标准差的平均值。k-fold评估在计算上的成本是昂贵的，但是对于小规模数据集来说还是非常有必要的，对于较小的数据集来说，错误的分割可能导致过于乐观（因为测试数据太简单）或过于悲观（因为测试数据太复杂）的情况。

5.3 知道什么时候停止训练

先前的例子使用固定次数的周期来训练模型，虽然这是最简单的方法，但它是任意并且不必要的。正确度量模型效果的一个关键功能是使用该度量来知道何时应该停止训练。最常用的方法是使用名为早停法（early stopping）的启发式方法。早停法通过跟踪验证数据集上从一个周期到另一个周期的效果以及注意效果何时不再改进来工作。然后，如果模型效果继续没有改善，训练将终止。在结束训练之前需要等待的周期数称为patience。一般来说，模型停止改进某些数据集的时间点称为模型收敛（converge）的时间点。在实际应用中，我们很少等模型完全收敛，因为收敛是耗时的，而且会导致过拟合。

5.4 找到正确的超参数

我们在前面了解到，一个参数（或权重）采用优化器关于称为小批量minibatch的固定训练数据子集所调整得到的实际值。一个超参数（hyperparameter）是影响模型中参数数量和参数所取值的模型设置。有许多不同的选择可以决定如何训练模型，它们包括选择一个损失函数、优化器、优化器的学习率（如layer的大小，将在第四章中讲解）、早停法的patience和各种正则化决策（也将在第四章中讨论）。需要注意的是，这些决策会对模型是否收敛及其效果产生很大影响，所以你应该系统地探索各种选择点。

5.5 正则化

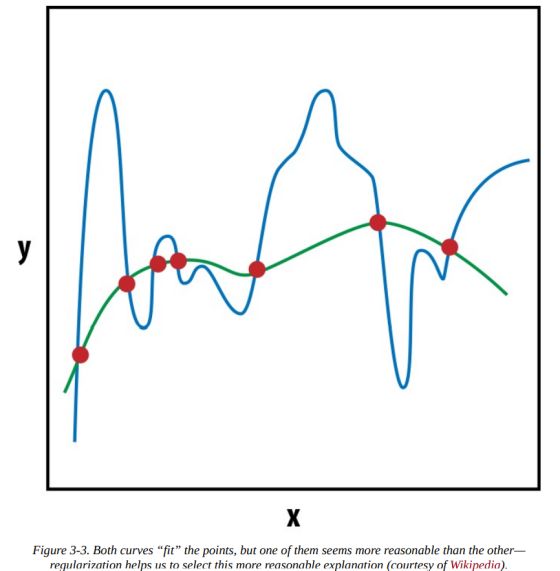
深度学习（以及普遍意义上的机器学习）中最重要的概念之一是正则化（regularization）。正则化的概念来源于数值优化理论。回想一下，大多数机器学习算法都在优化损失函数，以找到对于模型来说最可能的参数值，以解释观测结果（即产生的损失最少）。对于大多数数据集和任务，这个优化问题可能有多个解决方案（可能的模型）。那么我们（或优化器）应该选择哪一个模型呢？为了形成直观的理解，请考虑下图（3-3），它通过一组点拟合曲线：

两条曲线都拟合（fit）这些点，但哪一条是不太可能的解释呢？通过应用奥卡姆剃刀（Occam’s razor），我们可以凭直觉知道：一个简单的解释比复杂的解释更好。这种机器学习中的平滑约束称为 L2 正则化（L2 regularization）。在 PyTorch 中，你可以通过在优化器中设置weight_decay参数来控制这一点。weight_decay值越大，优化器选择的解释就越流畅，也即L2 正则化越强。

除了 L2，另一种流行的正则化是 L1 正则化（L1 regularization）。L1 通常用来鼓励稀疏解（sparser solutions），也就是说大多数模型参数值都接近于零。在第四章中，你将看到一种结构正则化技术，称为“dropout”。模型正则化是一个很活跃的研究领域，而PyTorch 是实现自定义正则化的灵活框架。