机器视觉：霍夫变换-理论与python实现

前言

这学期在学习机器视觉，课上讲到了霍夫变换，霍夫变换在图像处理和CV中很常用，借此十一假期仔细了解一下。
霍夫变换用来检测给定形状的曲线，其最开始是用来检测图像中的直线的，但经发展也可检测到圆等曲线。在目标检测中，如果不知图像中目标的位置而知道其轮廓的曲线方程，则可用霍夫变换进行检测。

霍夫变换—直线原理

在平面O-xy中，直线方程的基本形式为：y=ux+v。其中，u和v分别是直线的斜率和截距。对于一条确定的直线y=ux+v，它唯一地对应于平面O-uv中一个点（u，v）；反之，对于平面O-uv中给定的一个点（u，v），它唯一地确定了平面O-xy中的一条直线。这种线到点的变换就是Hough变换。
同理，平面O-uv中的一条直线v=-xu+y与O-xy中的一个点（x，y）也是一一对应的。
对于给定直线上的任意三点（i，i） ，i = 1，2，3，其中，（，）和（，）所对应的平面O-uv中的两条直线为
可以算得这两条直线的交点为：

点（，）和（，）所对应的两条直线为：

它们的交点为：

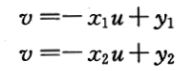
由此可以推知：直线y=ux+v上各点所对应的O-uv中的各直线交于一点 （u0，v0）。利用这个重要特性可以检测共线点。注意到直线的斜率可能有近于无穷大的情况，直线方程不用截斜式而釆用极坐标形式：

霍夫逆变换，theta变成t，rho变成r了，没找到合适公式，将就看吧（==）

其中，ρ是直线到坐标系原点的距离；θ是直线法线与x轴的夹角。于是，直角坐标平面O-xy中的一直线和极坐标平面O-ρθ中的点一一对应，O-xy中的共线点与对应的O-ρθ中的曲线交于一点。下图的（a）和（b）表示O-xy中的直线和O-ρθ中的点对应关系——Hough变换：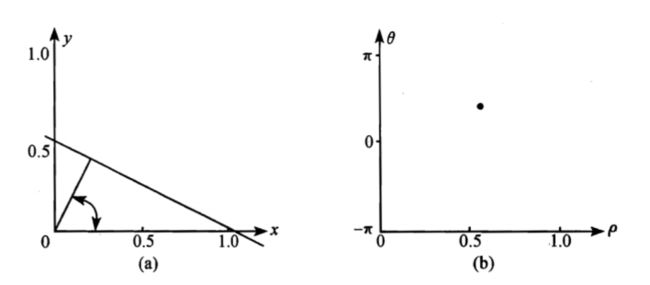

（c）和（d）表示O-xy中的点及共点线与O-ρθ中的曲线及曲线上点的对应关系：

（e）和（f）展示出了共线点所在直线对应于这些点在变换域中相应曲线的交点：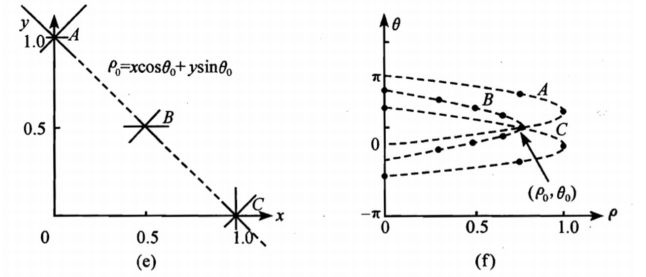

实现方法

根据精度要求将O-ρθ平面划分为等间隔的小直网格，这个直网格对应一个初始阵元为零的记数阵列。对于O-xy平面中的每一点，按上面介绍的原理在O-ρθ平面中画出它对应的曲线，凡是这条曲线所经过的小格，对应的计数阵列元素加1，通过同一小格的曲线所对应的点近乎共线，于是计数阵元的数值等于共线的点数。

有点难理解？翻译成人话就是：因为要把xy坐标系中的直线映射成ρθ坐标系中的点。 那就先反过来做，先在xy坐标系中找出图形所在的那些点，每个点都会在ρθ坐标系中映射成一条曲线（如图ef），如果这些点在xy坐标系中是共线的，那么它们在ρθ坐标系中映射的曲线是共点。如图e在直线中找出3点映射，则会在ρθ坐标系中映射成3条曲线，相交于一点。那么通过计数这个点经过的曲线个数，就可以知道在xy坐标系中有多少个点共线了。对应于大计数（数值很大）的小格，通过它的那些曲线在xy中对应的的点近乎共线，这里的（ρ，θ）可以作为拟合直线。
如果我们想检测图像中的直线，图像就是xy坐标系。在图像中实现检测有如下几个步骤：

1. 通过canny等边缘检测算子找到图像中直线经过的像素点映射到ρθ坐标系（网格近似）中，获得一条曲线；
2. 该曲线经过的像素点值+1；
3. 重复步骤1和2，遍历整个图形；
4. ρθ坐标系中每个元素中的数值代表图像共线的点数，数值较大的点可以作为拟合直线（ρ，θ）；
5. 霍夫逆变换求出原图直线

在选取网格时，若ρ，θ网格过小，即量化过细，虽然拟合直线的参数可以准确求出，但计算量加大了，且各组共线点数可能变少，因此要适当选取网格大小。

python实现

mport numpy as np 
import cv2 
from matplotlib import pyplot as plt 
from collections import Counter 

# 读取图像 
img = cv2.imread('line.png',2) 
img = 255 - img print(img.shape)  # [204,547] 

# 正变换：将xy坐标系中的点映射到极坐标中，记录映射函数经过的每一点 
def hough_forward_conver(x,y,points):     
	for t in range(0,360,2):         
		r = int(x * np.cos(np.pi*t/180) + y * np.sin(np.pi*t/180))         
		points.append([t,r])  # 直线经过的点放进去     
	return points     

# 反变换：根据极坐标系的坐标求xy坐标系的坐标 
def hough_reverse_conver(y, t,r):     
	x = int(- y * (np.sin(np.pi*t/180) / (np.cos(np.pi*t/180)+ 1e-4)) + r / (np.cos(np.pi*t/180)+1e-4))     
	return x   

# 霍夫正变换 
points = []  # 存放变换后的直线经过的点 
px, py = np.where(img == 255)  # 检测出直线上的点 
for x,y in zip(px,py):     
	points = hough_forward_conver(x,y,points)  # 霍夫变换，xy--->theta,rho 
print(len(points)) 

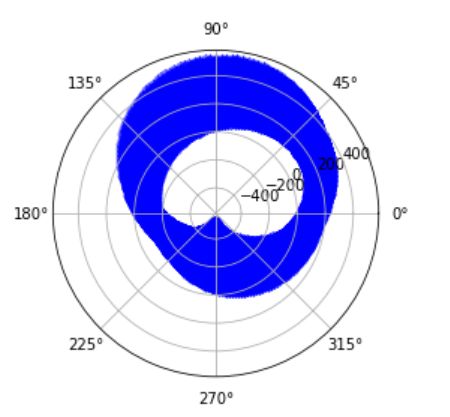
# 画极坐标图 
points = np.array(points) 
theta, rho = points[:,0], points[:,1] 
ax = plt.subplot(111, projection='polar') 
ax.scatter(np.pi*theta/180, rho, c='b', alpha=0.5,linewidths=0.01) 

# 霍夫空间的网格坐标系 
hough_space = np.zeros([360, 3000]) 
for point in points:
     t, r = point[0], point[1] + 1000  # r可能为负，防止索引溢出     h
     ough_space[t,r] += 1     

# 找出直线所在的点 
line_points = np.where(hough_space >= 15)
 print(len(line_points[0])) 

# 霍夫逆变换求xy 
mask = np.zeros_like(img) 
for t,r in zip(line_points[0],line_points[1]):
     for y in range(img.shape[0]):     
         x = hough_reverse_conver(y, t,r-1000)         
         if x in range(1,img.shape[1]):             
         	mask[y,x] += 1             

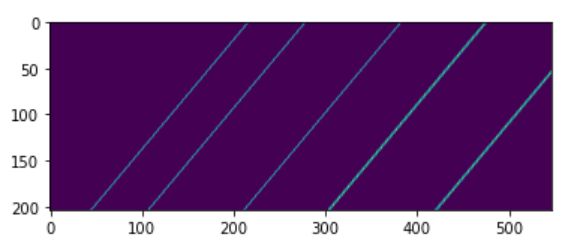
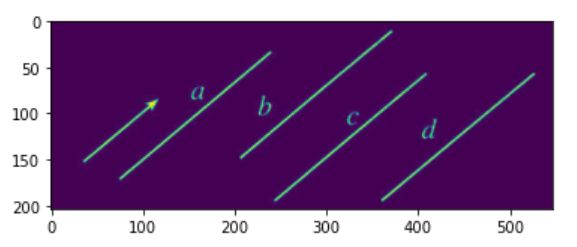
plt.imshow(mask) 
plt.imshow(img)

原图：