吴恩达机器学习(十八)—— ex7:K-means Clustering and Principal Component Analysis (MATLAB + Python)
吴恩达机器学习系列内容的学习目录 → \rightarrow →吴恩达机器学习系列内容汇总。
- 一、K-means聚类
-
- 1.1 实现K-means
-
- 1.1.1 找到最近的聚类中心
- 1.1.2 计算聚类中心均值
- 1.2 K-means用于样本数据集
- 1.3 随机初始化
- 1.4 使用K-means进行图像压缩
-
- 1.4.1 K-means用于像素
- 1.5 可选练习:使用自己的图像
- 二、主成分分析
-
- 2.1 样本数据集
- 2.2 实现PCA
- 2.3 用PCA减少维数
-
- 2.3.1 将数据投影到主成分上
- 2.3.2 重建数据的近似值
- 2.3.3 可视化投影
- 2.4 面部图像数据集
-
- 2.4.1 PCA用于面部
- 2.4.2 减少维度
- 2.5可选练习:PCA用于可视化
- 三、MATLAB实现
-
- 3.1 ex7.m
- 3.2 ex7_pca.m
- 四、Python实现
-
- 4.1 ex7.py
- 4.2 ex7_pca.py
本次练习对应的基础知识总结 → \rightarrow →聚类和降维。
本次练习对应的文档说明和提供的MATLAB代码 → \rightarrow → 提取码:cm24 。
本次练习对应的完整代码实现(MATLAB + Python版本) → \rightarrow →Github链接。
一、K-means聚类
在此练习中,我们将实现K-means算法并使用它进行图像压缩。我们将首先启动一个样本2D数据集,来帮助我们直观理解K-means算法是如何工作的。之后,使用K-means算法进行图像压缩,通过将图像中出现的颜色数量减少为仅图像中最常见的颜色。我们将在练习中使用ex7.m。
1.1 实现K-means
K-means算法是一种用于将类似数据样本自动聚集的方法。具体地,给出训练集 { x ( 1 ) , . . . , x ( m ) } \{ x^{(1)},...,x^{(m)}\} {x(1),...,x(m)}(其中 x ( i ) ∈ R n x^{(i)}∈R^{n} x(i)∈Rn),并且希望将数据分组成几个有凝聚力的“簇”。K-means的直观体现是一个迭代过程,它通过猜测初始聚类中心点(centroids)开始,然后重复地将样本分配给最接近的中心,基于分配来重新计算中心点。
K-means算法如下:
% Initialize centroids
centroids = kMeansInitCentroids(X, K);
for iter = 1:iterations
% Cluster assignment step: Assign each data point to the
% closest centroid. idx(i) corresponds to cˆ(i), the index
% of the centroid assigned to example i
idx = findClosestCentroids(X, centroids);
% Move centroid step: Compute means based on centroid
% assignments
centroids = computeMeans(X, idx, K);
end
算法的内部循环反复执行两个步骤:(i) 将每个训练样本 x ( i ) x^{(i)} x(i)分配给其最接近的聚类中心;(ii) 使用分配给它的点重新计算每个中心点的平均值。对于聚类中心,K-means算法总是收敛到最终的均值集。请注意,融合解决方案可能并不总是理想的,并且取决于聚类中心的初始设置。因此,实际上,K-means算法通常用不同的随机初始化运行几次,从不同的随机初始化中选择这些不同解决方案的一种方法是选择具有最低代价函数值(失真)的解决方案。
我们将在下一节中分开实现K-means算法的两个阶段。
1.1.1 找到最近的聚类中心
在K-means算法的“簇分配”阶段找到最近的聚类中心,算法把每个训练样本 x ( i ) x^{(i)} x(i)分配给其最接近的聚类中心,给出当前聚类中心位置。具体来说,对于每个样本 i i i
c ( i ) : = j t h a t m i n i m i z e s ∥ x ( i ) − μ i ∥ 2 c^{(i)} := j\ _{}\ _{}\ _{}\ _{}that\ _{}minimizes\ _{}\left \| x^{(i)}-\mu _{i} \right \|^{2} c(i):=j that minimizes ∥∥∥x(i)−μi∥∥∥2
其中 c ( i ) c^{(i)} c(i)是最接近 x ( i ) x^{(i)} x(i)的聚类中心的索引,以及 μ i \mu _{i} μi是第 j j j个聚类中心的位置(值)。请注意, c ( i ) c^{(i)} c(i)对应于开始代码中的idx(i)。
我们的任务是在findClosestCentroids.m中填写代码。此函数采用数据矩阵 X X X 和 c e n t r o i d s centroids centroids 内所有聚类中心的位置,并应输出一维数组 i d x idx idx,该数组包含每个训练样本的最近聚类中心的索引(值在 1 , … , K {1,…,K} 1,…,K中,其中 K K K是聚类中心总数)。
我们可以在每个训练样本和每个聚类中心上使用循环来实现此操作。
完成findClosestCentroids.m需要填写以下代码:
for i = 1:size(X,1)
dist = pdist([X(i,:);centroids]);%D=pdist(x) 计算m*n的数据矩阵中对象之间的欧几里得距离
dist =dist(:,1:K);%得到每一个样本到所有聚类中心的距离
[row, col] = find(dist == min(dist));
idx(i) = col(1);
end
完成findClosestCentroids.m中的代码后,脚本ex7.m将运行代码,我们应该看到与分配给前3个样本的聚类中心对应的输出[1 3 2]。
Finding closest centroids.
Closest centroids for the first 3 examples:
1 3 2
(the closest centroids should be 1, 3, 2 respectively)
1.1.2 计算聚类中心均值
给每个点分配一个聚类中心,算法重新计算的第二阶段,将各点的平均值分配给每个聚类中心。具体来说,对于我们的每个聚类中心 k k k
μ k : = 1 ∣ C k ∣ ∑ i ∈ C k x ( i ) \mu _{k}:=\frac{1}{\left | C_{k} \right |}\sum _{i\in C_{k}}x^{(i)} μk:=∣Ck∣1i∈Ck∑x(i)
其中 C k C_{k} Ck为分配给聚类中心 k k k的样本集。具体地,如果两个样本 x ( 3 ) x^{(3)} x(3)和 x ( 5 ) x^{(5)} x(5)被分配给聚类中心 k = 2 k = 2 k=2,则应更新 μ 2 = 1 2 ( x ( 3 ) + x ( 5 ) ) μ_{2}= \frac{1}{2}(x^{(3)}+ x^{(5)}) μ2=21(x(3)+x(5))。
我们现在应该在Computecentroids.m中填写代码。我们可以使用一个循环遍历聚类中心来实现此函数,还可以使用循环遍历样本。但是如果我们使用向量化实现而不是循环实现,则代码可能运行地更快。
完成Computecentroids.m需要填写以下代码:
for i = 1:K
centroids(i,:) = mean(X(find(idx == i),:));
end
完成Computecentroids中的代码后,脚本ex7.m将运行代码并在K-means的第一步之后输出聚类中心。
Computing centroids means.
Centroids computed after initial finding of closest centroids:
2.428301 3.157924
5.813503 2.633656
7.119387 3.616684
(the centroids should be
[ 2.428301 3.157924 ]
[ 5.813503 2.633656 ]
[ 7.119387 3.616684 ]
1.2 K-means用于样本数据集
实现函数findClosestCentroids和computeCentroids之后,ex7.m脚本的下一步将在玩具2D数据集上运行K-means算法,以帮助我们了解K-means是如何工作的。我们的函数从runKmeans.m脚本内部调用,可以查看函数以了解它的工作原理。请注意,代码调用我们在循环中实现的两个函数。
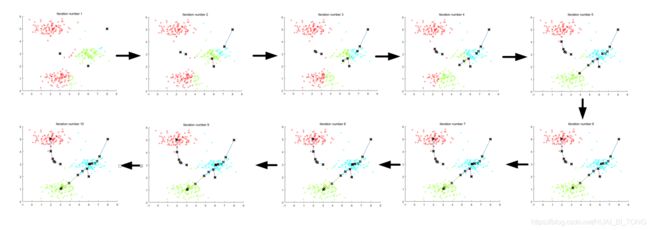
运行下一步时,K-means代码将产生可视化,在每次迭代时通过算法的进展来实现可视化。多次按enter键以查看K-means算法的每个步骤如何更改聚类中心和簇分配。最后,我们应该得到图1中所示的图。
运行过程输出如下图所示。
Running K-Means clustering on example dataset.
K-Means iteration 1/10...
Press enter to continue.
K-Means iteration 2/10...
Press enter to continue.
K-Means iteration 3/10...
Press enter to continue.
K-Means iteration 4/10...
Press enter to continue.
K-Means iteration 5/10...
Press enter to continue.
K-Means iteration 6/10...
Press enter to continue.
K-Means iteration 7/10...
Press enter to continue.
K-Means iteration 8/10...
Press enter to continue.
K-Means iteration 9/10...
Press enter to continue.
K-Means iteration 10/10...
Press enter to continue.
K-Means Done.
1.3 随机初始化
在ex7.m中样本数据集的聚类中心的初始分配是设计的,使得我们将看到与图1相同的图像。实际中,好的初始化聚类中心的策略是从训练集中选择随机样本。
在这部分练习中,我们应该用以下代码填写函数 kMeansInitCentroids.m:
% Initialize the centroids to be random examples
% Randomly reorder the indices of examples
randidx = randperm(size(X, 1));
% Take the first K examples as centroids
centroids = X(randidx(1:K), :);
上面的代码首先对样本的索引进行随机排列(使用randperm)。然后,它基于索引的随机排列选择前 K K K个样本。这允许随意选择要选择的样本,而不会出现两次选择相同样本的风险。
1.4 使用K-means进行图像压缩
在本练习中,我们将应用K-means进行图像压缩。在图像直接的24位颜色表示中,每个像素表示为三个8位无符号整数(范围为0到255),其指定红色、绿色和蓝色强度值,该编码通常被称为RGB编码。我们的图像包含数千种颜色,在这部分练习中,我们将把颜色的数量减少到16种。
通过这种减少,可以以有效的方式表示(压缩)照片。具体地说,我们只需要存储16种选定颜色的RGB值,对于图像中的每个像素,我们现在只需要存储该位置的颜色索引(其中仅需要4位来表示16种可能性)。
在本练习中,我们将使用K-means算法选择将用于表示压缩图像的16种颜色。具体地,我们将把原始图像中的每个像素视为数据样本,并使用K-means算法找到在3维RGB空间中最佳组(簇)像素的16种颜色。一旦我们计算出图像上的聚类中心后,我们将使用16种颜色替换原始图像中的像素。
1.4.1 K-means用于像素
在MATLAB中,可以按如下方式读取图像:
% Load 128x128 color image (bird small.png)
A = imread('bird small.png');
% You will need to have installed the image package to used
% imread. If you do not have the image package installed, you
% should instead change the following line to
%
% load('bird small.mat'); % Loads the image into the variable A
这将创建三维矩阵A,其前两个索引表示像素位置,最后索引表示红色、绿色或蓝色。例如,A(50,33,3)给出了50行、33列的像素的蓝色强度。
ex7.m中的代码首先加载图像,然后重新创建像素颜色的 m × 3 m×3 m×3矩阵(其中 m = 16384 = 128 × 128 m = 16384 = 128×128 m=16384=128×128),并调用K-means函数。
原始的128x128图像如图2所示。
在查找前 K = 16 K = 16 K=16种颜色以表示图像后,我们现在可以使用findClosestCentroids函数分配每个像素位置到最近的聚类中心。这允许我们使用每个像素的聚类中心分配来表示原始图像。请注意,我们已显着减少描述图像所需的字节数。对于128×128像素位置中的每一个,所需的原始图像需要24位,使得总尺寸为128×128×24 = 393,216位。新的表示需要以16种颜色字典的形式进行一些开销存储,每个形式需要24位,但图像本身只需要每像素位置4位。所使用的最终字节数为16×24 + 128×128×4 = 65,920位,其对应于将原始图像压缩大约6倍。
最后,我们可以通过仅基于聚类中心分配的重建图像来查看压缩的影响。具体来说,我们可以用分配给每个像素位置的聚类中心的平均值替换每个像素位置。图3显示了我们获得的重建。即使所得到的图像保留了原始的大部分特征,我们也看到了一些压缩损伤。
1.5 可选练习:使用自己的图像
在本练习中使用自己的图像,修改提供的代码以在自己的图像上运行。请注意,如果自己的图像非常大,则K-means可能需要很长时间才能运行。因此,建议在运行代码之前将图像的大小调整为可管理的大小,也可以尝试改变 K K K来查看对压缩的影响。
二、主成分分析
在本练习中,我们将使用主成分分析(PCA)来实现维数减少。我们将首先尝试使用样本2D数据集以获得PCA如何工作的直观理解,然后在5000个面部图像的更大数据集上使用它。
提供的脚本ex7_pca.m将帮助我们开始练习的前半部分。
2.1 样本数据集
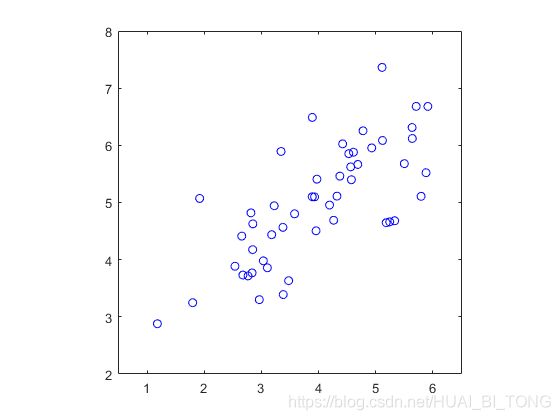
为了从直观上了解PCA的工作原理,首先从2D数据集开始,该数据集具有一个大的变化方向和一个较小的变化。脚本ex7_pca.m将绘制训练数据(图4)。在这一部分练习中,我们将可视化在使用PCA将数据从2D降至1D时发生的事情。实际中,我们可能希望将数据从256降至50维,但是在该样本中使用较低维的数据允许我们更好地可视化算法。
2.2 实现PCA
在这部分练习中,我们将实现PCA。 PCA由两个计算步骤组成:首先,计算数据的协方差矩阵;然后,使用MATLAB的svd函数来计算特征向量 U 1 , U 2 , . . . U n U_{1},U_{2},...U_{n} U1,U2,...Un。这些将对应于数据变化的主成分。
在使用PCA之前,重要的是首先通过从数据集中减去每个特征的平均值来归一化数据,并缩放每个维度,使它们处于同一范围内。在提供的脚本ex7_pca.m中,使用featureNormalize函数对特征进行了归一化。
归一化数据后,我们可以运行PCA来计算主成分。我们的任务是在pca.m中完成代码以计算数据集的主成分。首先,我们应该计算数据的协方差矩阵:
Σ = 1 m X T X \Sigma =\frac{1}{m}X^{T}X Σ=m1XTX
其中 X X X是行中样本的数据矩阵,而 m m m是样本的数量。注意, Σ Σ Σ是 n × n n×n n×n矩阵而不是求和操作。
计算协方差矩阵后,我们可以运行SVD来计算主成分。在MATLAB中,我们可以使用以下命令运行SVD:[U,S,V] = svd(Sigma),其中U将包含主成分,S将包含对角线矩阵。
完成pca.m需要填写以下代码:
Sigma = X'*X./m;
[U,S,~] = svd(Sigma);
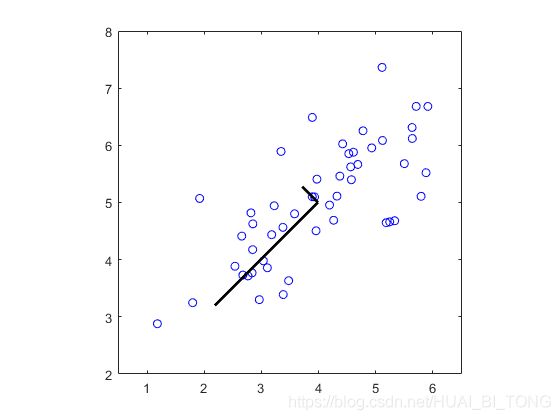
完成pca.m后,ex7_pca.m脚本将在样本数据集上运行PCA,并绘制找到的相应主成分(图5)。该脚本还将输出找到的顶部主成分(特征向量),并且我们应该期望看到大约[-0.707 -0.707]的输出。
Running PCA on example dataset.
Top eigenvector:
U(:,1) = -0.707107 -0.707107
(you should expect to see -0.707107 -0.707107)
2.3 用PCA减少维数
计算主成分后,我们可以使用它们来减少数据集的特征维度,通过将每个样本投影到较低维度空间, x ( i ) → z ( i ) x^{(i)}→z^{(i)} x(i)→z(i)(例如,从2D到1D投影数据)。在练习的这一部分中,我们将使用PCA返回的特征向量,并将样本数据集投影到1维空间。
实际中,如果我们使用的是线性回归或神经网络等学习算法,我们现在可以使用投影数据而不是原始数据。通过使用投影数据,我们可以更快地训练模型,因为输入中的尺寸较小。
2.3.1 将数据投影到主成分上
我们现在应该在projectData.m中填写代码。具体地,给定数据集 X X X,主成分 U U U和维度减少到 K K K所需的数量。我们应该将 X X X中的每个样本投射到 U U U的前 K K K个成分上。注意,通过 U U U的前 K K K列给出了 U U U的前 K K K个成分,U_reduce = U(:, 1:K)。
完成projectData.m需要填写以下代码:
Z = X*U(:,1:K);
完成projectData.m中的代码后,ex7_pca.m将第一个样本投影到第一个维度上,我们应该看到约1.481的值(或者可能为-1.481,如果我们用 − U 1 -U_{1} −U1代替 U 1 U_{1} U1)。
Dimension reduction on example dataset.
Projection of the first example: 1.481274
(this value should be about 1.481274)
2.3.2 重建数据的近似值
将数据投影到较低维度空间后,我们可以通过将它们投影出回原始的高维空间来近似恢复数据。我们的任务是完成recoverData.m以将Z的每个样本投影回原始空间,并返回X_rec中的恢复近似值。
完成recoverData.m需要填写以下代码:
X_rec = Z*U(:,1:K)';
完成recoverData.m中的代码后,ex7_pca.m将恢复第一个样本的近似值,我们应该看到约[-1.047 -1.047]的值。
Approximation of the first example: -1.047419 -1.047419
(this value should be about -1.047419 -1.047419)
2.3.3 可视化投影
完成函数projectData和recoverData后,ex7_pca.m现在将实现投影和近似重建以显示投影如何影响数据。在图6中,原始数据点用蓝圆圈表示,而投影的数据点用红色圆圈表示。投影只有效地保留了U1给出的方向上的信息。
2.4 面部图像数据集
在练习的这一部分中,我们将在脸部图像上运行PCA,以了解如何在实际中使用维度减少。数据集ex7faces.mat包含32×32的灰度脸部图像的数据集 X X X。每行X对应于一个面部图像(长度为1024的行向量)。
ex7_pca.m的下一步将加载和可视化这些面部图像的前100个(图7)。
2.4.1 PCA用于面部
要在面部数据集上运行PCA,我们首先通过从数据矩阵 X X X中减去每个特征的平均值来归一化数据集。脚本ex7_pca.m将为我们执行此操作,然后运行PCA代码。运行PCA后,我们将获得数据集的主成分。请注意,U(每行)中的每个主成分是长度为 n n n的向量(用于面部数据集, n = 1024 n = 1024 n=1024)。事实证明,我们可以通过将它们中的每一个重塑为32×32矩阵来可视化这些主成分,该矩阵对应于原始数据集中的像素。脚本ex7_pca.m显示描述最大变化的前36个主成分(图8)。如果需要,我们还可以更改代码以显示更多主成分,以查看它们如何捕获越来越多的详细信息。
2.4.2 减少维度
既然已经计算了面部数据集的主成分,可以使用它来减少面部数据集的维度。这允许我们使用较小的输入大小(例如,100维)而不是原始的1024维的学习算法,有助于加快学习算法。
ex7_pca.m的下一部分将对面部数据集投影到前100主成分上。具体地,现在通过向量 Z ( i ) ∈ R 100 Z^{(i)}∈R^{100} Z(i)∈R100来描述每个面部图像。
要了解维度降低中丢失的内容,可以使用投影数据集来恢复数据。在ex7_pca.m中,实现数据的近似恢复,并且原始和投影的面部图像并排显示(图9)。从重建来看,我们可以观察到虽然细节丢失,但脸部的一般结构和外观依然在。在数据集大小中,这是一个显着的减少(超过10×),可以帮助显着加快学习算法。例如,如果我们正在训练一个神经网络以实现人员识别(给定一张面部图像,预测人的身份),则可以使用减少到仅100维的维度而不是原始像素。
2.5可选练习:PCA用于可视化
在第一节中的K-means图像压缩练习中,已经在三维RGB空间中使用了K-means算法。在ex7_pca.m脚本的最后一部分中,我们使用scatter3函数(三维散点图函数)可视化此3D空间中的最终像素分配,每个数据点根据已分配给它的集群进行着色,如图10所示。我们可以将鼠标拖到图上以旋转并在3个维度中检查此数据。

事实证明,3维或更高维的可视化数据集可能是麻烦的。因此,即使以丢失某些信息为代价,通常也仅希望在2维中显示数据。实际中,PCA通常为了可视化的目的,用于减少数据的维度。在ex7_pca.m的下一部分中,脚本将应用PCA的实现使3维数据减少到2维,并在2维散点图中可视化结果,如图11所示。 PCA投影可以被认为是选择最大化数据传播视图的旋转,这通常对应于“最佳”视图。
三、MATLAB实现
3.1 ex7.m
%% Machine Learning Online Class
% Exercise 7 | Principle Component Analysis and K-Means Clustering
%
% Instructions
% ------------
%
% This file contains code that helps you get started on the
% exercise. You will need to complete the following functions:
%
% pca.m
% projectData.m
% recoverData.m
% computeCentroids.m
% findClosestCentroids.m
% kMeansInitCentroids.m
%
% For this exercise, you will not need to change any code in this file,
% or any other files other than those mentioned above.
%
%% Initialization
clear ; close all; clc
%% ================= Part 1: Find Closest Centroids ====================
% To help you implement K-Means, we have divided the learning algorithm
% into two functions -- findClosestCentroids and computeCentroids. In this
% part, you should complete the code in the findClosestCentroids function.
%
fprintf('Finding closest centroids.\n\n');
% Load an example dataset that we will be using
load('ex7data2.mat');
% Select an initial set of centroids
K = 3; % 3 Centroids
initial_centroids = [3 3; 6 2; 8 5];
% Find the closest centroids for the examples using the
% initial_centroids
idx = findClosestCentroids(X, initial_centroids);%findClosestCentroids()计算每个样本的聚类中心
fprintf('Closest centroids for the first 3 examples: \n')
fprintf(' %d', idx(1:3));
fprintf('\n(the closest centroids should be 1, 3, 2 respectively)\n');
fprintf('Program paused. Press enter to continue.\n');
pause;
%% ===================== Part 2: Compute Means =========================
% After implementing the closest centroids function, you should now
% complete the computeCentroids function.
%
fprintf('\nComputing centroids means.\n\n');
% Compute means based on the closest centroids found in the previous part.
centroids = computeCentroids(X, idx, K);%computeCentroids()通过计算分配给每个质心的数据点的平均值,返回新质心
fprintf('Centroids computed after initial finding of closest centroids: \n')
fprintf(' %f %f \n' , centroids');
fprintf('\n(the centroids should be\n');
fprintf(' [ 2.428301 3.157924 ]\n');
fprintf(' [ 5.813503 2.633656 ]\n');
fprintf(' [ 7.119387 3.616684 ]\n\n');
fprintf('Program paused. Press enter to continue.\n');
pause;
%% =================== Part 3: K-Means Clustering ======================
% After you have completed the two functions computeCentroids and
% findClosestCentroids, you have all the necessary pieces to run the
% kMeans algorithm. In this part, you will run the K-Means algorithm on
% the example dataset we have provided.
%
fprintf('\nRunning K-Means clustering on example dataset.\n\n');
% Load an example dataset
load('ex7data2.mat');
% Settings for running K-Means
K = 3;
max_iters = 10;
% For consistency, here we set centroids to specific values
% but in practice you want to generate them automatically, such as by
% settings them to be random examples (as can be seen in
% kMeansInitCentroids).
initial_centroids = [3 3; 6 2; 8 5];
% Run K-Means algorithm. The 'true' at the end tells our function to plot the progress of K-Means
[centroids, idx] = runkMeans(X, initial_centroids, max_iters, true);%runkMeans()在数据矩阵X上运行K-Means算法,其中X的每一行是一个样本
fprintf('\nK-Means Done.\n\n');
fprintf('Program paused. Press enter to continue.\n');
pause;
%% ============= Part 4: K-Means Clustering on Pixels ===============
% In this exercise, you will use K-Means to compress an image. To do this,
% you will first run K-Means on the colors of the pixels in the image and
% then you will map each pixel onto its closest centroid.
%
% You should now complete the code in kMeansInitCentroids.m
%
fprintf('\nRunning K-Means clustering on pixels from an image.\n\n');
% Load an image of a bird
A = double(imread('bird_small.png'));%处理图像像素点数据,matlab读入图像的数据是uint8,而数值一般采用double型(64位)存储和运算,所以要先将图像转为double格式的才能运算
% If imread does not work for you, you can try instead
% load ('bird_small.mat');
A = A / 255; % Divide by 255 so that all values are in the range 0 - 1
% Size of the image
img_size = size(A);
% Reshape the image into an Nx3 matrix where N = number of pixels.
% Each row will contain the Red, Green and Blue pixel values
% This gives us our dataset matrix X that we will use K-Means on.
X = reshape(A, img_size(1) * img_size(2), 3);%X为128x128x3
% Run your K-Means algorithm on this data
% You should try different values of K and max_iters here
K = 16;
max_iters = 10;
% When using K-Means, it is important the initialize the centroids randomly.
% You should complete the code in kMeansInitCentroids.m before proceeding
initial_centroids = kMeansInitCentroids(X, K);
% Run K-Means
[centroids, idx] = runkMeans(X, initial_centroids, max_iters);
fprintf('Program paused. Press enter to continue.\n');
pause;
%% ================= Part 5: Image Compression ======================
% In this part of the exercise, you will use the clusters of K-Means to
% compress an image. To do this, we first find the closest clusters for
% each example. After that, we
fprintf('\nApplying K-Means to compress an image.\n\n');
% Find closest cluster members
idx = findClosestCentroids(X, centroids);
% Essentially, now we have represented the image X as in terms of the indices in idx.
% We can now recover the image from the indices (idx) by mapping each pixel
% (specified by its index in idx) to the centroid value
%我们现在可以从索引(idx)中恢复图像,方法是将每个像素(由idx中的索引指定)映射到质心值
X_recovered = centroids(idx,:);
% Reshape the recovered image into proper dimensions
X_recovered = reshape(X_recovered, img_size(1), img_size(2), 3);
% Display the original image
subplot(1, 2, 1);
imagesc(A); %imagesc(A) 将矩阵A中的元素数值按大小转化为不同颜色,并在坐标轴对应位置处以这种颜色染色
title('Original');
% Display compressed image side by side
subplot(1, 2, 2);
imagesc(X_recovered)
title(sprintf('Compressed, with %d colors.', K));
3.2 ex7_pca.m
%% Machine Learning Online Class
% Exercise 7 | Principle Component Analysis and K-Means Clustering
%
% Instructions
% ------------
%
% This file contains code that helps you get started on the
% exercise. You will need to complete the following functions:
%
% pca.m
% projectData.m
% recoverData.m
% computeCentroids.m
% findClosestCentroids.m
% kMeansInitCentroids.m
%
% For this exercise, you will not need to change any code in this file,
% or any other files other than those mentioned above.
%
%% Initialization
clear ; close all; clc
%% ================== Part 1: Load Example Dataset ===================
% We start this exercise by using a small dataset that is easily to
% visualize
%
fprintf('Visualizing example dataset for PCA.\n\n');
% The following command loads the dataset. You should now have the
% variable X in your environment
load ('ex7data1.mat');
% Visualize the example dataset
plot(X(:, 1), X(:, 2), 'bo');
axis([0.5 6.5 2 8]); axis square;
fprintf('Program paused. Press enter to continue.\n');
pause;
%% =============== Part 2: Principal Component Analysis ===============
% You should now implement PCA, a dimension reduction technique. You
% should complete the code in pca.m
%
fprintf('\nRunning PCA on example dataset.\n\n');
% Before running PCA, it is important to first normalize X
[X_norm, mu, sigma] = featureNormalize(X);
% Run PCA
[U, S] = pca(X_norm);%pca()在数据集X上运行主成分分析
% Compute mu, the mean of the each feature
% Draw the eigenvectors centered at mean of data. These lines show the
% directions of maximum variations in the dataset.
hold on;
drawLine(mu, mu + 1.5 * S(1,1) * U(:,1)', '-k', 'LineWidth', 2);
drawLine(mu, mu + 1.5 * S(2,2) * U(:,2)', '-k', 'LineWidth', 2);
hold off;
fprintf('Top eigenvector: \n');
fprintf(' U(:,1) = %f %f \n', U(1,1), U(2,1));
fprintf('\n(you should expect to see -0.707107 -0.707107)\n');
fprintf('Program paused. Press enter to continue.\n');
pause;
%% =================== Part 3: Dimension Reduction ===================
% You should now implement the projection step to map the data onto the
% first k eigenvectors. The code will then plot the data in this reduced
% dimensional space. This will show you what the data looks like when
% using only the corresponding eigenvectors to reconstruct it.
%
% You should complete the code in projectData.m
%
fprintf('\nDimension reduction on example dataset.\n\n');
% Plot the normalized dataset (returned from pca)
plot(X_norm(:, 1), X_norm(:, 2), 'bo');
axis([-4 3 -4 3]); axis square
% Project the data onto K = 1 dimension
K = 1;
Z = projectData(X_norm, U, K);
fprintf('Projection of the first example: %f\n', Z(1));
fprintf('\n(this value should be about 1.481274)\n\n');
X_rec = recoverData(Z, U, K);
fprintf('Approximation of the first example: %f %f\n', X_rec(1, 1), X_rec(1, 2));
fprintf('\n(this value should be about -1.047419 -1.047419)\n\n');
% Draw lines connecting the projected points to the original points
hold on;
plot(X_rec(:, 1), X_rec(:, 2), 'ro');
for i = 1:size(X_norm, 1)
drawLine(X_norm(i,:), X_rec(i,:), '--k', 'LineWidth', 1);
end
hold off
fprintf('Program paused. Press enter to continue.\n');
pause;
%% =============== Part 4: Loading and Visualizing Face Data =============
% We start the exercise by first loading and visualizing the dataset.
% The following code will load the dataset into your environment
%
fprintf('\nLoading face dataset.\n\n');
% Load Face dataset
load ('ex7faces.mat')
% Display the first 100 faces in the dataset
displayData(X(1:100, :));
fprintf('Program paused. Press enter to continue.\n');
pause;
%% =========== Part 5: PCA on Face Data: Eigenfaces ===================
% Run PCA and visualize the eigenvectors which are in this case eigenfaces
% We display the first 36 eigenfaces.
%
fprintf(['\nRunning PCA on face dataset.\n' ...
'(this might take a minute or two ...)\n\n']);
% Before running PCA, it is important to first normalize X by subtracting
% the mean value from each feature
[X_norm, mu, sigma] = featureNormalize(X);
% Run PCA
[U, S] = pca(X_norm);
% Visualize the top 36 eigenvectors found
displayData(U(:, 1:36)');% 绘出前36个特征向量
fprintf('Program paused. Press enter to continue.\n');
pause;
%% ============= Part 6: Dimension Reduction for Faces =================
% Project images to the eigen space using the top k eigenvectors
% If you are applying a machine learning algorithm
fprintf('\nDimension reduction for face dataset.\n\n');
K = 100;%将面部数据集投影到前100个中心成分上
Z = projectData(X_norm, U, K);
fprintf('The projected data Z has a size of: ')
fprintf('%d ', size(Z));
fprintf('\n\nProgram paused. Press enter to continue.\n');
pause;
%% ==== Part 7: Visualization of Faces after PCA Dimension Reduction ====
% Project images to the eigen space using the top K eigen vectors and
% visualize only using those K dimensions
% Compare to the original input, which is also displayed
fprintf('\nVisualizing the projected (reduced dimension) faces.\n\n');
K = 100;
X_rec = recoverData(Z, U, K);
% Display normalized data
subplot(1, 2, 1);
displayData(X_norm(1:100,:));
title('Original faces');
axis square;
% Display reconstructed data from only k eigenfaces
subplot(1, 2, 2);
displayData(X_rec(1:100,:));
title('Recovered faces');
axis square;
fprintf('Program paused. Press enter to continue.\n');
pause;
%% === Part 8(a): Optional (ungraded) Exercise: PCA for Visualization ===
% One useful application of PCA is to use it to visualize high-dimensional
% data. In the last K-Means exercise you ran K-Means on 3-dimensional
% pixel colors of an image. We first visualize this output in 3D, and then
% apply PCA to obtain a visualization in 2D.
close all; close all; clc
% Reload the image from the previous exercise and run K-Means on it
% For this to work, you need to complete the K-Means assignment first
A = double(imread('bird_small.png'));
% If imread does not work for you, you can try instead
% load ('bird_small.mat');
A = A / 255;
img_size = size(A);
X = reshape(A, img_size(1) * img_size(2), 3);
K = 16;
max_iters = 10;
initial_centroids = kMeansInitCentroids(X, K);
[centroids, idx] = runkMeans(X, initial_centroids, max_iters);
% Sample 1000 random indexes (since working with all the data is
% too expensive. If you have a fast computer, you may increase this.
sel = floor(rand(1000, 1) * size(X, 1)) + 1;
% Setup Color Palette
palette = hsv(K);%c = hsv(m) 返回包含 m 种颜色的颜色图 palette为16x3
colors = palette(idx(sel), :);
% Visualize the data and centroid memberships in 3D
figure;
scatter3(X(sel, 1), X(sel, 2), X(sel, 3), 10, colors);%scatter3函数:三维散点图函数
title('Pixel dataset plotted in 3D. Color shows centroid memberships');
fprintf('Program paused. Press enter to continue.\n');
pause;
%% === Part 8(b): Optional (ungraded) Exercise: PCA for Visualization ===
% Use PCA to project this cloud to 2D for visualization
% Subtract the mean to use PCA
[X_norm, mu, sigma] = featureNormalize(X);
% PCA and project the data to 2D
[U, S] = pca(X_norm);
Z = projectData(X_norm, U, 2);%projectData()在X中绘制数据点,并将它们着色,以便在idx中具有相同的index赋值的那些点具有相同的颜色
% Plot in 2D
figure;
plotDataPoints(Z(sel, :), idx(sel), K);
title('Pixel dataset plotted in 2D, using PCA for dimensionality reduction');
四、Python实现
4.1 ex7.py
import numpy as np
import matplotlib.pylab as plt
import scipy.io as sio
import matplotlib.colors as pltcolor
# ================= Part 1: Find Closest Centroids ====================
# 找出最邻近点
def findCloseCenter(x, center):
k, l = np.shape(center)
xtemp = np.tile(x, k)#Numpy的 tile() 函数,就是将原矩阵横向(x倍)、纵向地复制(k倍)
centertemp = center.flatten()
xtemp = np.power(xtemp-centertemp, 2)
xt = np.zeros((np.size(xtemp, 0), k))
for i in range(k):
for j in range(l):
xt[:, i] = xt[:, i]+xtemp[:, i*l+j]
idx = np.argmin(xt, 1)+1
return idx
print('Finding closest centroids.')
datainfo = sio.loadmat('ex7data2.mat')
X = datainfo['X']
K = 3
init_center = np.array([[3, 3], [6, 2], [8, 5]])
idX = findCloseCenter(X, init_center)
print('Closest centroids for the first 3 examples: ', idX[0:3])
print('(the closest centroids should be 1, 3, 2 respectively)')
_ = input('Press [Enter] to continue.')
# ===================== Part 2: Compute Means =========================
# 找出中心点
def computeCenter(x, idx, k):
m, n = np.shape(x)
center = np.zeros((k, n))
for i in range(k):
pos = np.where(idx == i+1)
center[i, :] = np.sum(x[pos], 0)/np.size(x[pos], 0)
return center
print('Computing centroids means.')
center = computeCenter(X, idX, K)
print('Centroids computed after initial finding of closest centroids: ')
print(center)
print('the centroids should be: ')
print('[[ 2.428301 3.157924 ], [ 5.813503 2.633656 ], [ 7.119387 3.616684 ]]')
_ = input('Press [Enter] to continue.')
# =================== Part 3: K-Means Clustering ======================
# 中心点连线
def drawLine(p1, p2):
x = np.array([p1[0], p2[0]])
y = np.array([p1[1], p2[1]])
plt.plot(x, y)
# 绘制数据点
def plotDataPoints(x, idx, k):
colors = ['red', 'green', 'blue']
plt.scatter(x[:, 0], x[:, 1], c=idx, cmap=pltcolor.ListedColormap(colors), s=40)
# 绘制中心点
def plotProgresskMeans(x, center, previous, idx, k, i):
plotDataPoints(x, idx, k)
plt.plot(center[:, 0], center[:, 1], 'x', ms=10, mew=1)
for j in range(np.size(center, 0)):
drawLine(center[j, :], previous[j, :])
plt.title('Iteration number %d' % (i+1))
# k均值聚类
def runkMeans(x, init_center, max_iter, plot_progress=False):
m, n = np.shape(x)
k = np.size(init_center, 0)
center = init_center
previous_center = center
idx = np.zeros((m,))
if plot_progress:
plt.ion()
fig = plt.figure()
for i in range(max_iter):
print('K-Means iteration %d/%d...' % (i+1, max_iter))
idx = findCloseCenter(x, center)
if plot_progress:
plotProgresskMeans(x, center, previous_center, idx, k, i)
previous_center = center
fig.canvas.draw()
_ = input('Press [Enter] to continue.')
center = computeCenter(x, idx, k)
plt.show(block=True)
plt.ioff()
return center, idx
print('Running K-Means clustering on example dataset.')
max_iter = 10
K = 3
init_center = np.array([[3, 3], [6, 2], [8, 5]])
center, idx = runkMeans(X, init_center, max_iter, True)
print('K-Means Done.')
_ = input('Press [Enter] to continue.')
# ============= Part 4: K-Means Clustering on Pixels ===============
# 生成初始点
def kMeansInitCenter(x, k):
randidx = np.random.permutation(np.size(x, 0))
center = x[randidx[0: k], :]
return center
print('Running K-Means clustering on pixels from an image.')
A = plt.imread('bird_small.png')
m, n, l = np.shape(A)
A_x = np.reshape(A, (m*n, l))
A_k = 16
A_max_iter = 10
A_init_center = kMeansInitCenter(A_x, A_k)
A_center, A_idx = runkMeans(A_x, A_init_center, A_max_iter)
print(A_center)
_ = input('Press [Enter] to continue.')
# ================= Part 5: Image Compression ======================
print('Applying K-Means to compress an image.')
A_idx = findCloseCenter(A_x, A_center)
X_recovered = A_center[A_idx-1, :]
X_back = X_recovered.reshape(m, n, l)
fig = plt.figure()
ax1 = fig.add_subplot(121)
ax1.imshow(A)
ax1.set_title('Original')
ax2 = fig.add_subplot(122)
ax2.imshow(X_back)
ax2.set_title('Compressed, with %d colors.' % A_k)
plt.show(block=False)
4.2 ex7_pca.py
import numpy as np
import matplotlib.pylab as plt
import scipy.io as sio
import numpy.linalg as la
import math
import matplotlib.cm as cm
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.colors as pltcolor
# ================== Part 1: Load Example Dataset ===================
print('Visualizing example dataset for PCA.')
datainfo = sio.loadmat('ex7data1.mat')
X = datainfo['X']
plt.plot(X[:, 0], X[:, 1], 'bo')
plt.axis([0.5, 6.5, 2, 8])
plt.axis('equal')
_ = input('Press [Enter] to continue.')
# =============== Part 2: Principal Component Analysis ===============
# 归一化
def featureNormalize(x):
mu = np.mean(x, 0)
sigma = np.std(x, 0, ddof=1)
x_norm = (x-mu)/sigma
return x_norm, mu, sigma
# pca
def pca(x):
m, n = np.shape(x)
sigma = 1/m*x.T.dot(x)
u, s, _ = la.svd(sigma)
return u, s
# 两点连线
def drawLine(p1, p2, lc='k-', lwidth=2):
x = np.array([p1[0], p2[0]])
y = np.array([p1[1], p2[1]])
plt.plot(x, y, lc, lw=lwidth)
print('Running PCA on example dataset.')
x_norm, mu, sigma = featureNormalize(X)
u, s = pca(x_norm)
drawLine(mu, mu+1.5*s[0]*u[:, 0])
drawLine(mu, mu+1.5*s[1]*u[:, 1])
plt.show()
print('Top eigenvector: ')
print(' U(:,1) = %f %f ' %(u[0, 0], u[1, 0]))
print('(you should expect to see -0.707107 -0.707107)')
_ = input('Press [Enter] to continue.')
# =================== Part 3: Dimension Reduction ===================
# 映射数据
def projectData(x, u, k):
z = x.dot(u[:, 0:k])
return z
# 数据复原
def recoverData(z, u, k):
x_rec = np.asmatrix(z).dot(u[:, 0:k].T)
return np.asarray(x_rec)
print('Dimension reduction on example dataset.')
plt.plot(x_norm[:, 0], x_norm[:, 1], 'bo')
plt.axis([-4, 3, -4, 3])
plt.axis('equal')
k = 1
z = projectData(x_norm, u, k)
print('Projection of the first example: ', z[0])
print('(this value should be about 1.481274)')
x_rec = recoverData(z, u, k)
print('Approximation of the first example: %f %f' % (x_rec[0, 0], x_rec[0, 1]))
plt.plot(x_rec[:, 0], x_rec[:, 1], 'ro')
for i in range(np.size(x_norm, 0)):
drawLine(x_norm[i, :], x_rec[i, :], 'k--', 1)
plt.show()
_ = input('Press [Enter] to continue.')
# =============== Part 4: Loading and Visualizing Face Data =============
# 显示数据
def displayData(x):
width = round(math.sqrt(np.size(x, 1)))
m, n = np.shape(x)
height = int(n/width)
# 显示图像的数量
drows = math.floor(math.sqrt(m))
dcols = math.ceil(m/drows)
pad = 1
# 建立一个空白“背景布”
darray = -1*np.ones((pad+drows*(height+pad), pad+dcols*(width+pad)))
curr_ex = 0
for j in range(drows):
for i in range(dcols):
if curr_ex >= m:
break
max_val = np.max(np.abs(x[curr_ex, :]))
darray[pad+j*(height+pad):pad+j*(height+pad)+height, pad+i*(width+pad):pad+i*(width+pad)+width]\
= x[curr_ex, :].reshape((height, width))/max_val
curr_ex += 1
if curr_ex >= m:
break
plt.imshow(darray.T, cmap='gray')
print('Loading face dataset.')
datainfo = sio.loadmat('ex7faces.mat')
X = datainfo['X']
displayData(X[0:100, :])
plt.show()
_ = input('Press [Enter] to continue.')
# =========== Part 5: PCA on Face Data: Eigenfaces ===================
print('Running PCA on face dataset\n(this mght take a minute or two ...)')
x_norm, mu, sigma = featureNormalize(X)
u, s = pca(x_norm)
displayData(u[:, 0:36].T)
plt.show()
_ = input('Press [Enter] to continue.')
# ============= Part 6: Dimension Reduction for Faces =================
print('Dimension reduction for face dataset.')
K = 100
Z = projectData(x_norm, u, K)
print('the project data Z has a size of ', np.shape(Z))
_ = input('Press [Enter] to continue.')
# ==== Part 7: Visualization of Faces after PCA Dimension Reduction ====
print('Visualizing the projected (reduced dimension) faces.')
X_rec = recoverData(Z, u, K)
fig = plt.figure()
plt.subplot(121)
displayData(x_norm[0:100, :])
plt.title('Original faces')
plt.subplot(122)
displayData(X_rec[0:100, :])
plt.title('Recovered faces')
plt.show()
_ = input('Press [Enter] to continue.')
# === Part 8(a): Optional (ungraded) Exercise: PCA for Visualization ===
# 生成初始点
def kMeansInitCenter(x, k):
randidx = np.random.permutation(np.size(x, 0))
center = x[randidx[0: k], :]
return center
# 找出最邻近点
def findCloseCenter(x, center):
k, l = np.shape(center)
xtemp = np.tile(x, k)
centertemp = center.flatten()
xtemp = np.power(xtemp-centertemp, 2)
xt = np.zeros((np.size(xtemp, 0), k))
for i in range(k):
for j in range(l):
xt[:, i] = xt[:, i]+xtemp[:, i*l+j]
idx = np.argmin(xt, 1)+1
return idx
# 找出中心点
def computeCenter(x, idx, k):
m, n = np.shape(x)
center = np.zeros((k, n))
for i in range(k):
pos = np.where(idx == i+1)
center[i, :] = np.sum(x[pos], 0)/np.size(x[pos], 0)
return center
# k均值聚类
def runkMeans(x, init_center, max_iter):
m, n = np.shape(x)
k = np.size(init_center, 0)
center = init_center
idx = np.zeros((m,))
for i in range(max_iter):
idx = findCloseCenter(x, center)
center = computeCenter(x, idx, k)
return center, idx
A = plt.imread('bird_small.png')
img_size = np.shape(A)
X = A.reshape(img_size[0]*img_size[1], img_size[2])
K = 16
max_iter = 10
init_center = kMeansInitCenter(X, K)
center, idx = runkMeans(X, init_center, max_iter)
sel = np.floor(np.random.random((1000,))*np.size(X, 0)).astype(int)+1
colors = cm.rainbow(np.linspace(0, 1, K))
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[sel, 0], X[sel, 1], X[sel, 2], c=idx[sel], cmap=pltcolor.ListedColormap(colors), marker='o')
ax.set_title('Pixel dataset plotted in 3D. Color shows centroid memberships')
plt.show()
_ = input('Press [Enter] to continue.')
# === Part 8(b): Optional (ungraded) Exercise: PCA for Visualization ===
X_norm, mu, sigma = featureNormalize(X)
u, s = pca(X_norm)
Z = projectData(X_norm, u, 2)
colors = cm.rainbow(np.linspace(0, 1, K))
plt.scatter(Z[sel, 0], Z[sel, 1], c=idx[sel], cmap=pltcolor.ListedColormap(colors), marker='o')
plt.title('Pixel dataset plotted in 2D, using PCA for dimensionality reduction')
plt.show()