隐马尔可夫模型HMM+维特比算法(Viterbi Algorithm)进行词性标注代码实现(自然语言处理课程第二次作业)
文章目录
- 一、理论描述
- 二、算法描述
- 三、详例描述
-
- 具体过程
-
- 分析题目
- 数据预处理
-
- 转移概率矩阵:
- 发射概率矩阵:
- HMM+维特比算法进行词性标注
-
- 开始进行词性标注:
-
- The:
- bear:
- is:
- on:
- the:
- move:
- 标注结果
- 四、软件演示(完整代码及运行结果)
-
- 关键代码
- 完整代码
- 运行结果
- 五、参考链接
-
- python实现
- Java实现
一、理论描述
隐马尔可夫模型是马尔可夫链的一种,它的状态不能直接观察到,但能通过观测向量序列观察到,每个观测向量都是通过某些概率密度分布表现为各种状态,每一个观测向量是由一个具有相应概率密度分布的状态序列产生。所以,隐马尔可夫模型是一个双重随机过程----具有一定状态数的隐马尔可夫链和显示随机函数集。自20世纪80年代以来,HMM被应用于语音识别,取得重大成功。到了90年代,HMM还被引入计算机文字识别和移动通信核心技术“多用户的检测”。HMM在生物信息科学、故障诊断等领域也开始得到应用。
HMM 是一个五元组(O,Q,O0,A,B) :
O:{o1 … ot } 是状态集合,也称为观测序列
Q:{q1 … qv } 是一组输出结果,也称隐序列
aij =P(qj |qi ): 转移概率分布
bij =P(oj |qi ): 发射概率分布
O0是初始状态,有些还有终止状态维特比算法是以部分最优去获得全局最优,每个节点保存的是当前节点的局部最优概率,依据最后一个时刻中概率最高的状态,逆向找其路径中的上一个最大部分最优路径,从而找到整个最优路径。
二、算法描述
观察序列长度 T,状态个数N
for 状态s from 1 to N:do
//计算每个状态的概率,相当于计算第一观察值的隐状态t=1
v[s,1] = a(0,s)*b(O1|s) //初始状态概率 * 发射概率
//回溯保存最大概率状态
back[s,1]=0
//计算每个观察(词语)取各个词性的概率,保存最大者
for from 观察序列第二个 to T do:
for 状态s from 1 to N:do
//当前状态由前一个状态*转移*发射(该状态/词性下词t的概率),保存最大者
v[s,t]=max v[i,t-1]*a[i,s]*b(Ot | s)
//保存回溯点,该点为前一个状态转移到当前状态的最大概率点
back[s,t]=arg{1,N} max v[i,t-1]*a(i,s)
//最后
v[T]=max v[T]
back[T] = arg{1,N} max v[T]
//回溯输出隐状态序列
三、详例描述
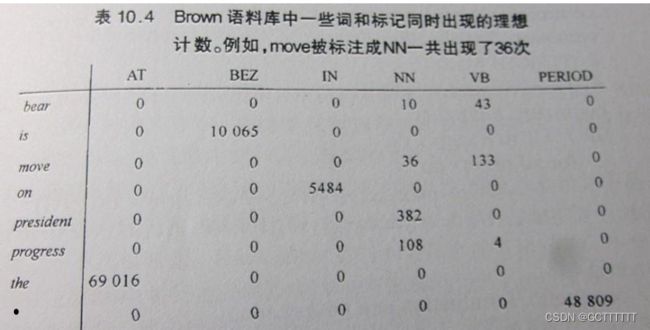
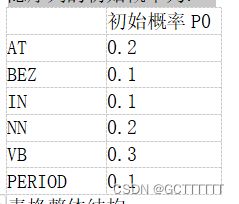
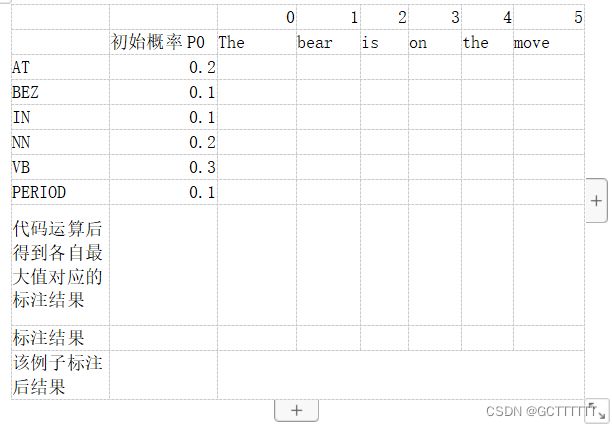
假定初始概率为:
AT BEZ IN NN VB PERIOD
[0.2 0.1 0.1 0.2 0.3 0.1]依据以上两个表格,使用 HMM 和 和 Viterbi 算法标注下面的句子。
The bear is on the move
具体过程
分析题目
分析该例子,可知
观测序列O为: O:{The, bear, is, on, the, move}
隐序列Q为:Q:{AT,BEZ,IN,NN,VB,PERIOD}
数据预处理
上面的两个原始表格中:
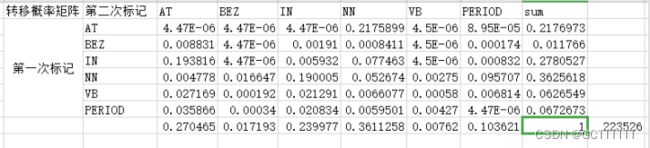
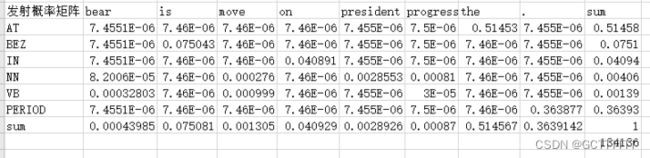
第一个表格在进行数据平滑(表格中每个数+1)后、再对每个数除以该表格各个数相加的和即得到 转移概率矩阵而第二个表格需要先将表格转置,再对数据进行平滑(表格中每个数+1)、将每个数除以该表格各个数相加的和即得到发射概率矩阵
将第一个表格中数据平滑后得到如下矩阵:

将第二个表格中数据(进行转置处理后)平滑后得到如下矩阵:

将处理后的两个矩阵中数值分别求和后,将每个单元格内的数除以各自对应矩阵求和后的值,得到转移概率矩阵和发射概率矩阵:
转移概率矩阵:
发射概率矩阵:
解释:
上面两个矩阵中,
例如转移概率Z[AT][AT]=4.47E-06,Z[BEZ][IN]=0.00191,
发射概率F[AT][BEAR]=7.4551E-06,F[VB][MOVE]=0.000999
HMM+维特比算法进行词性标注
假设:
初始概率P0
概率P
转移概率Z
发射概率F
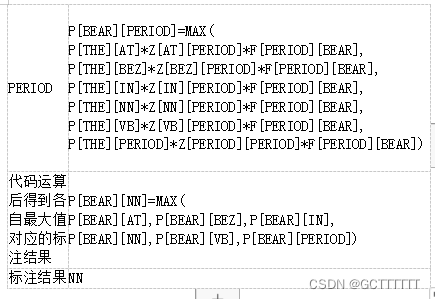
开始进行词性标注:
The:
bear:
is:
on:
the:
move:
标注结果
由上述过程可知{The, bear, is, on, the, move}最后的标注结果为:
[‘the/AT’, ‘bear/NN’, ‘is/BEZ’, ‘on/IN’, ‘the/AT’, ‘move/NN’]
四、软件演示(完整代码及运行结果)
关键代码
维特比算法相关关键代码:
def vierbi(obs, states, start_p, trans_p, emit_p):
"""
:param obs: 观察序列 K
:param states: 隐藏状态 S
:param start_p: 初始概率 π
:param trans_p: 转移概率 A
:param emit_p: 发射概率 B
:return:
"""
# 路径概率表 V[时间][隐状态] = 概率
V = [{}]
# 一个中间变量,代表当前状态是哪个隐状态
path = {}
# 初始化初始状态 t=0
for y in states:
V[0][y] = start_p[y] * emit_p[y][obs[0]]
path[y] = [y]
# 对t>0 跑一遍维特比算法
for t in range(1, len(obs)):
V.append({})
newpath = {}
for y in states:
# 概率 隐状态 = 前状态是y0的概率 * y0转移到y的概率 * y表现为当前状态的概率
(prob, state) = max([(V[t - 1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) for y0 in states])
# 记录最大概率
V[t][y] = prob
# 记录路径
newpath[y] = path[state] + [y]
# 不需要保存旧路径
path = newpath
print_dptable(V)
(prob, state) = max([(V[len(obs) - 1][y], y) for y in states])
return prob, path[state]
完整代码
(python实现)
# -*- coding:utf-8 -*-
"""
维特比算法的实现
HMM 五个重要元素
S 隐藏序列的集合
K 输出状态或观测状态的集合
π对应隐藏状态的的初始概率
A 隐藏状态的转移概率 是一个N*M的概率矩阵
B 隐藏状态到观测状态的混淆矩阵,是一个N*M的发射概率的矩阵
"""
# 隐藏序列 S
# states = ("Rainy", "Sunny")
states = ('AT', 'BEZ', 'IN','NN','VB','PERIOD')
# 观测序列 K
# observations = ('walk', 'shop', 'clean')
observations = ("the", "bear","is","on","the","move")
# print(observations)
# print(result)
# 初始概率 π
# start_probability = {'Rainy': 0.6, "Sunny": 0.4}
start_probability = {'AT':0.2, 'BEZ':0.1, 'IN':0.1,'NN':0.2,'VB':0.3,'PERIOD':0.1}
sumA = 223499
# 转移概率 A
transition_probability = {
# 'Rainy': {"Rainy": 0.7, "Sunny": 0.3},
# "Sunny": {"Rainy": 0.4, "Sunny": 0.6}
"AT": {'AT': 1/sumA, 'BEZ': 1/sumA, 'IN': 1/sumA,'NN': 48636/sumA,'VB': 1/sumA,'PERIOD': 20/sumA},
"BEZ": {'AT': 1974/sumA, 'BEZ': 1/sumA, 'IN': 427/sumA,'NN': 188/sumA,'VB': 1/sumA,'PERIOD': 39/sumA},
"IN": {'AT': 43323/sumA, 'BEZ': 1/sumA, 'IN': 1326/sumA,'NN': 17315/sumA,'VB': 1/sumA,'PERIOD': 186/sumA},
"NN": {'AT': 1068/sumA, 'BEZ': 3721/sumA, 'IN': 42471/sumA,'NN': 11774/sumA,'VB': 615/sumA,'PERIOD': 21393/sumA},
"VB": {'AT': 6073/sumA, 'BEZ': 43/sumA, 'IN': 4759/sumA,'NN': 1477/sumA,'VB': 130/sumA,'PERIOD': 1523/sumA},
"PERIOD": {'AT': 8017/sumA, 'BEZ': 76/sumA, 'IN': 4657/sumA,'NN': 1330/sumA,'VB': 955/sumA,'PERIOD': 1/sumA}
}
# print(transition_probability['AT']['AT'])
sumB = 134136
# 发射概率 B
emission_probability = {
"AT": {'the': 69017/sumB, 'bear': 1/sumB, 'is': 1/sumB,'on': 1/sumB,'the': 69017/sumB,'move': 1/sumB},
"BEZ": {'the': 1/sumB, 'bear': 1/sumB, 'is': 10066/sumB,'on': 1/sumB,'the': 1/sumB,'move': 1/sumB},
"IN": {'the': 1/sumB, 'bear': 1/sumB, 'is': 1/sumB,'on': 5485/sumB,'the': 1/sumB,'move': 1/sumB},
"NN": {'the': 1/sumB, 'bear': 11/sumB, 'is': 1/sumB,'on': 1/sumB,'the': 1/sumB,'move': 37/sumB},
"VB": {'the': 1/sumB, 'bear': 44/sumB, 'is': 1/sumB,'on': 1/sumB,'the': 1/sumB,'move': 134/sumB},
"PERIOD": {'the': 1/sumB, 'bear': 1/sumB, 'is': 1/sumB,'on': 1/sumB,'the': 1/sumB,'move': 1/sumB}
}
def print_dptable(V):
print(" ")
for i in range(len(V)): print("%7d" % i, end="")
print()
for y in V[0].keys():
# print("%.5s: " % y, end=" ")
print("%-.30s: " % y, end=" ")
for t in range(len(V)):
# print("%.7s" % V[t][y], end=" ")
print("%-.30s" % V[t][y], end=" ")
print()
def vierbi(obs, states, start_p, trans_p, emit_p):
"""
:param obs: 观察序列 K
:param states: 隐藏状态 S
:param start_p: 初始概率 π
:param trans_p: 转移概率 A
:param emit_p: 发射概率 B
:return:
"""
# 路径概率表 V[时间][隐状态] = 概率
V = [{}]
# 一个中间变量,代表当前状态是哪个隐状态
path = {}
# 初始化初始状态 t=0
for y in states:
V[0][y] = start_p[y] * emit_p[y][obs[0]]
path[y] = [y]
# 对t>0 跑一遍维特比算法
for t in range(1, len(obs)):
V.append({})
newpath = {}
for y in states:
# 概率 隐状态 = 前状态是y0的概率 * y0转移到y的概率 * y表现为当前状态的概率
(prob, state) = max([(V[t - 1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) for y0 in states])
# 记录最大概率
V[t][y] = prob
# 记录路径
newpath[y] = path[state] + [y]
# 不需要保存旧路径
path = newpath
print_dptable(V)
(prob, state) = max([(V[len(obs) - 1][y], y) for y in states])
return prob, path[state]
# print(vierbi(observations,
# states,
# start_probability,
# transition_probability,
# emission_probability
# ))
result_org = observations
tag = vierbi(observations,
states,
start_probability,
transition_probability,
emission_probability
)
print(tag)
result = []
for i in range(len(result_org)):
result.append(result_org[i]+"/"+tag[1][i])
print("例句:")
print(observations)
print("标注结果:")
print(result)
运行结果
例句(‘the’, ‘bear’, ‘is’, ‘on’, ‘the’, ‘move’)的标注结果为:
[‘the/AT’, ‘bear/NN’, ‘is/BEZ’, ‘on/IN’, ‘the/AT’, ‘move/NN’]
五、参考链接
python实现
viterbi-algorithm 维特比算法的例子解析
Java实现
Java实现:抛开jieba等工具,写HMM+维特比算法进行词性标注