HMM-Viterbi algorithm(Python实现)
求解最可能的隐状态序列是HMM的三个典型问题之一,通常用维特比算法解决。维特比算法就是求解HMM上的最短路径(-log(prob),也即是最大概率)的算法。
算法思路:
- 从状态t到初始状态,需要寻找最短路径,运用逆推递归的方法来寻找这条最短路径。
- 状态t由状态(t-1)直接决定,从状态(t-1)到状态t一定有一条最短路径,问题的求解就变成了求初始状态到状态(t-1)的最短路径。
- 一直逆推到初始状态,问题就变成了求从初始状态到状态1的n条路径,然后找出状态1到状态2的最短的n条路径(实际上会有n*n条路径),一直递归到状态t,从最短的n条路径里寻找真正的最短路径。
该图(图片来源: 通俗易懂讲解HMM(隐马尔可夫模型))清晰地显示了隐马模型的状态转移过程: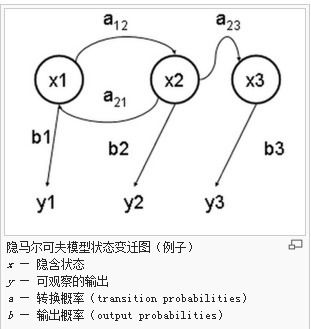
下面展示Viterbi algorithm 的完整代码(Python)。
import numpy as np
#寻找最短路径(最大概率)函数
def maxpossibilitypath(obs,states,start_p,trans_p,emit_p):
path = np.zeros((len(states),len(obs))) #存储路径
finalpath = np.zeros((len(states),len(obs))) #用于路径的位置更换
fp = np.zeros((len(obs))) #输出最终的路径
maxp = np.zeros((len(obs),len(states))) #存储第n次的m种路径长度(即概率)
max_p = 0 #用于作比较
for i in range(len(start_p)): #第一次状态输出
k = obs[0]
maxp[0][i] = start_p[i]*emit_p[i][k] #第一次发生状态x的概率
path[i][0] = i
finalpath[i][0] = i
max_p = 0
for i in range(len(start_p)): #将各条路径长度(概率)作比较 得出最优路径
if (maxp[0][i]>max_p):
max_p = maxp[0][i]
fp = path[i]
# maxp[0] = max_p
for i in range(len(obs)-1):
for j in range(len(states)):
max_p = 0
for k in range(len(states)):
if(maxp[i][k] * trans_p[k][j] * emit_p[j][(obs[i+1])] > max_p): #第i+1次时各路径长度
max_p = maxp[i][k] * trans_p[k][j] * emit_p[j][(obs[i+1])]
maxp[i+1][j] = max_p
path[k][i+1] = j #因为第i+1次继承了第i次的k状态,所以只需在路径k上更改第i+1的值
finalpath[j] = path[k]#赋值给flinalpath是为了让path与maxp的位置对应
max_p = 0
for l in range(len(states)):
if (maxp[i+1][l] > max_p):
max_p = maxp[i+1][l]
fp = finalpath[l]
path[l] = finalpath [l] #因为前一个循环的path修改只对第i+1次做更新,所以需要对path进行更新再做下一次循环,否则会出现错误
return(fp)
#隐状态
hidden_state = ['rainy', 'sunny']
#观测序列
obsevition = ['walk', 'shop', 'clean']
#隐状态对应的数字
state_s = [0, 1]
#实际观测的序列 walk:0 shop:1 clean:2
obser = [0,1,2,0,1,2,1,1,1,1,1,0,0,0,2,1,0,1,1,0,2,2,1]
#初始状态,测试集中,0.6概率观测序列以rainy开始
start_probability = [0.6, 0.4]
#转移概率
transititon_probability = np.array([[0.7, 0.3], [0.4, 0.6]])
#发射概率
emission_probability = np.array([[0.1, 0.4, 0.5], [0.6, 0.3, 0.1]])
result = maxpossibilitypath(obser, state_s, start_probability, transititon_probability, emission_probability)
print(result)
for k in range(len(result)):
d = int(result[k])
print(hidden_state[d])
天气转移概率矩阵
| rainy | sunny | |
|---|---|---|
| rainy | 0.7 | 0.3 |
| rainy | 0.4 | 0.6 |
每种天气(隐状态)对应行为(可观测)的概率矩阵
| walk | shop | clean | |
|---|---|---|---|
| rainy | 0.1 | 0.4 | 0.5 |
| rainy | 0.6 | 0.3 | 0.1 |
最终输出结果
[1. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 1. 1. 1. 0. 0. 1. 1. 1. 1. 0. 0. 0.]
sunny rainy rainy sunny rainy rainy rainy rainy rainy rainy rainy sunny sunny sunny rainy rainy sunny sunny sunny sunny rainy rainy rainy
初学Python,代码的实现比较笨拙。这也是本人第一次发表文章,有很多纰漏,还望大家多多包涵,谢谢!!!