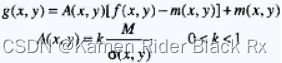数字图像处理报告：实验2 图像增强：直方图均衡、分块直方图均衡、局部直方图均衡、局部增强、USM虚光蒙版、双边滤波

• 实验2 图像增强：直方图均衡、分块直方图均衡、局部直方图均衡、局部增强、USM虚光蒙版、双边滤波

• 实验主题:

编程实现图像增强，完成直方图均衡、分块直方图均衡、局部直方图均衡、局部增强、USM虚光蒙版、双边滤波

• 实验目的:

1．掌握图像增强基本原理和方法。

2．学习使用程序设计环境。

3．使用设计框架构造应用程序。

4．掌握直方图均衡、分块直方图均衡、局部直方图均衡、局部增强、USM虚光蒙版、双边滤波的实现。

• 实验平台：

1. 编程工具：MATLAB R2020b
2. 编程语言：matlab

• 实验要求：

根据选择的图像，利用算法程序对其进行增强处理，对比增强前后图进行主客观2方面的评估。

• 实验代码：

%1.直方图均衡

%1.直方图均衡
I = imread('小豆泥.jpeg');
J = histeq(I);
 
figure;
subplot(221);imshow(I);
subplot(222);imshow(J);
subplot(223);imhist(I);
subplot(224);imhist(J);

%2.分块直方图均衡

%2.分块直方图均衡
img = imread('小豆泥.jpeg');
Img = SubHisteq(img);
 
figure;
subplot(221);imshow(img);
subplot(222);imshow(Img);
% subplot(223);imhist(img);
% subplot(224);imhist(Img);

function Img = SubHisteq(img)
[rows,cols]=size(img);
n=4;    %分成4*4块子图分别均衡
r=floor(rows/n);
c=floor(cols/n);
Img = zeros(rows,cols,'uint8');
for i=1:n
    for j=1:n
        Img((i-1)*r+1:i*r,(j-1)*c+1:j*c) = Histeq(img((i-1)*r+1:i*r,(j-1)*c+1:j*c));
    end
end
end

function Img = Histeq(img)
[~, F] = Hist(img);
Img=uint8(F(uint8(img+0.5))*255+0.5); %经过修改的
end

%3.局部直方图均衡

%3.局部直方图均衡
img = imread('小豆泥.jpeg');
Img = LocalHisteq(img);
 
figure;
subplot(221);imshow(img);
subplot(222);imshow(Img);
subplot(223);imhist(img);
subplot(224);imhist(Img);

function Img = LocalHisteq(img)
[rows,cols]=size(img);
h=128;
Img=zeros(rows,cols,'uint8');
for i=1:rows
    i0=max(1,i-h);
    i1=min(i+h,rows);
    for j=1:cols
        j0=max(1,j-h);
        j1=min(j+h,cols);
        if j==1
            H = FastHist(false,img(i0:i1,j0:j1),[],[],[]);
        else
            if j0==1
                out=[];
            else
                out=img(i0:i1,j0-1);
            end
            if j+h>cols
                in=[];
            else
                in=img(i0:i1,j1);
            end
            H = FastHist(true,[],H,in,out);
        end
        F = zeros(1,256);
        F(1) = H(1);
        for k=2:256
            F(k) = F(k-1)+H(k);
        end
        Img(i,j) = uint8(F(uint8(img(i,j)+0.5))*255/(i1-i0)/(j1-j0)+0.5);
    end
end
end

function H = FastHist(fast, img, h, in, out)
if ~fast
    n=numel(img);
    H=zeros(1,256);
    for i=1:n
        H(1+img(i))=H(1+img(i))+1;  %灰度值统计计数
    end
else
    H = h;
    n = numel(in);
    for i=1:n
        H(1+in(i))=H(1+in(i))+1;
    end
    n = numel(out);
    for i=1:n
        H(1+out(i))=H(1+out(i))-1;
    end
end
end

%4.局部增强

%4.局部增强
img=imread('img1.png');
figure('Name','原图');
imshow(img);
Img=LocalEnhance(img,15);
figure('Name','局部增强');
imshow(Img);

function Img = LocalEnhance(img,w)
h=round( (w-1)/2 );
[row,col,channel]=size(img);
Img=zeros(row,col,channel);
imgd=double(img);
for k=1:channel    %对每个颜色分量进行处理
    gvar=std2(imgd(:,:,k));  %计算全局标准差，作为图像全局对比度参考
    for i=1:row
        i0=max(1,i-h);
        i1=min(row,i+h);
        for j=1:col
            j0=max(1,j-h);
            j1=min(col,j+h);
            len=(i1-i0+1)*(j1-j0+1);
            m=sum(sum(imgd(i0:i1,j0:j1,k)))/len;         %邻域均值
            lvar=sqrt(sum(sum((imgd(i0:i1,j0:j1,k)-m).^2))/(len-1));        %计算局部区域标准差
            if gvar>4*lvar      %计算局部增强系数a，最大不值超过4，防止过增强导致失真
                a=4;
            else
                a=gvar/lvar;
            end
            Img(i,j,k)=a*(imgd(i,j,k)-m)+m;
        end
    end
end
Img=uint8(round(Img));
end

%5.USM虚光蒙版

%5.USM虚光蒙版
img=imread('x.png');
USM(img);

function Img = USM(img)
imgd=double(img);
 
sigma=50;
gausFilter = fspecial('gaussian',[30 30],sigma);
blur=imfilter(imgd,gausFilter,'replicate');
figure('Name','高斯模糊');
imshow(blur/max(blur(:)));
 
mask=imgd-blur;
figure('Name','蒙版');
imshow(mask/max(mask(:)));
 
Img=imgd+mask*0.7;
Img=Img/max(Img(:))*255;
Img=uint8(Img);
 
figure('Name','USM');
imshow(Img);
end

%6.双边滤波

%6.双边滤波
img = ones(32,512,'uint8')*200;
img = [img;img-150];
img = repmat(img,8,1);
img = imnoise(img, 'gaussian', 0, 0.01);
figure(1);
imshow(img);
 
Img = gausFilter(img, 5);
figure(2);
imshow(Img);
 
Img = BilateralFilter(img, 5, 25);
figure(3);
imshow(Img);

function Img = BilateralFilter(img, r, d)
imgd=double(img);
[row,col]=size(img);
h=2*r;
wr=ones(h*2+1,h*2+1);  %计算高斯平滑滤波核
for i=1:2*h+1
    for j=1:2*h+1
        wr(i,j)=exp( -((i-1-h)^2+(j-1-h)^2)/2/r^2 );
    end
end
 
Img=zeros(row,col);
for i=1:row
    i0=max(i-h,1);
    i1=min(i+h,row);
    I0=1+h - (i-i0);
    I1=1+h + (i1-i);
    for j=1:col
        j0=max(j-h,1);
        j1=min(j+h,col);
        J0=1+h - (j-j0);
        J1=1+h + (j1-j);
        
        B=imgd(i0:i1,j0:j1);    %取出待处理像素的邻域子图像
        C=B-imgd(i,j);          %扣除待处理中心像素值得到灰度差值矩阵
        C=exp(-C.^2/2/d^2);     %计算灰度权值矩阵
        C=C.*wr(I0:I1,J0:J1);   %灰度权值乘以距离权值
        C=C/sum(C(:));          %C为权值矩阵
        Img(i,j)=sum(sum(B.*C));
    end
end
Img=uint8(round(Img));
end

function Img = gausFilter(img,r)
[row,col]=size(img);
h=2*r;
wr=ones(h*2+1,h*2+1);  %计算高斯平滑滤波核
for i=1:2*h+1
    for j=1:2*h+1
        wr(i,j)=exp( -((i-1-h)^2+(j-1-h)^2)/2/r^2 );
    end
end
wr=wr/sum(wr(:));
 
imgd=double(img);
Img=zeros(row,col);
for i=1:row
    i0=max(1,i-h);
    i1=min(row,i+h);
    I0=1+h - (i-i0);
    I1=1+h + (i1-i);
    for j=1:col
        j0=max(1,j-h);
        j1=min(col,j+h);
        J0=1+h - (j-j0);
        J1=1+h + (j1-j);
        B=imgd(i0:i1,j0:j1).*wr(I0:I1,J0:J1);    %取出待处理像素的邻域子图像并同高斯模板相乘
        Img(i,j)=sum(B(:));
    end
end
Img=uint8(round(Img));
end

• 实验结果：

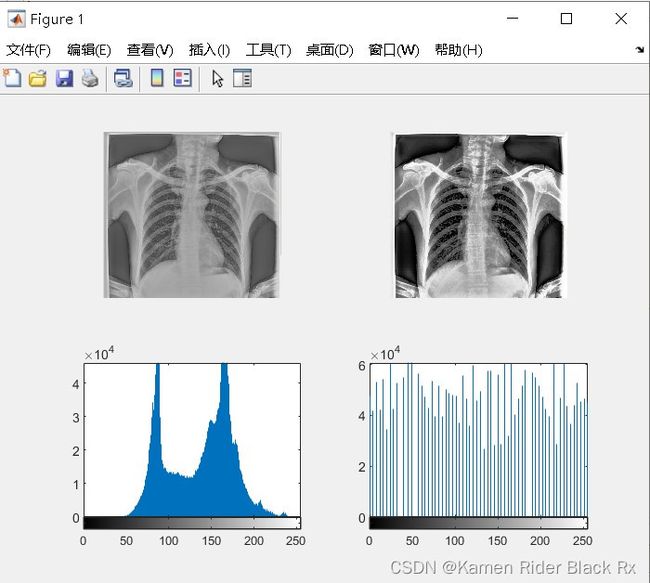
1. 直方图均衡 

 

图1-1 直方图均衡

        2.分块直方图均衡

 

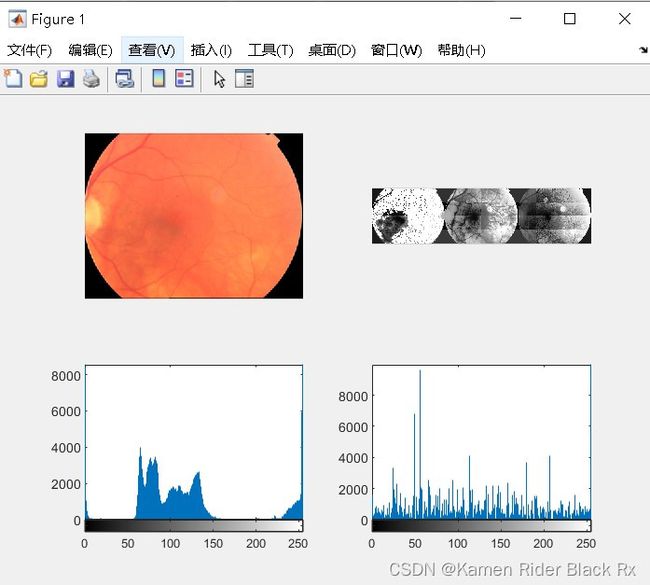
图2-1 分块直方图均衡 

        3.局部直方图均衡

 

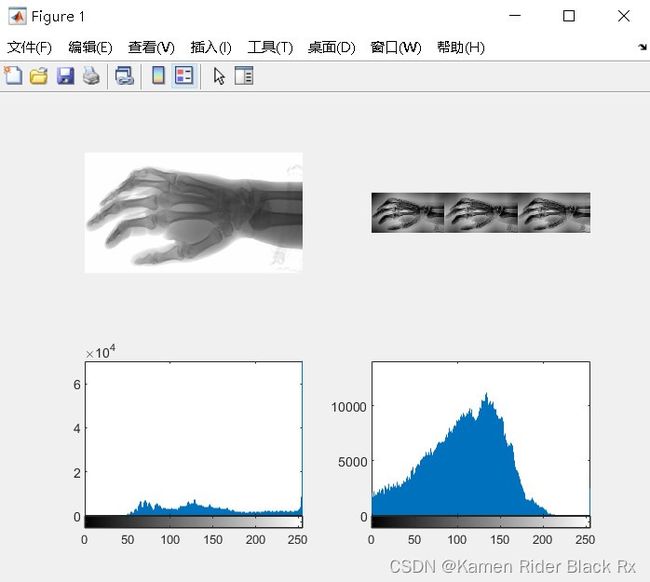
图3-1 局部直方图均衡

 

        4.局部增强

 

 

图4-1 局部增强

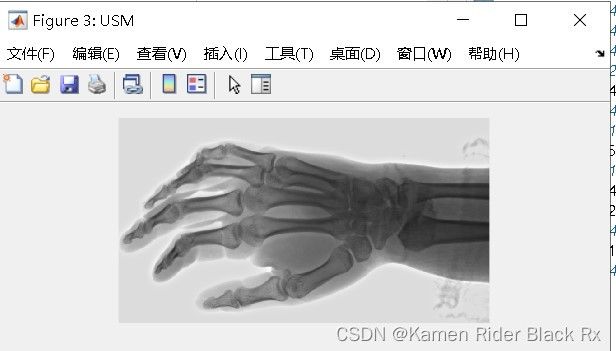
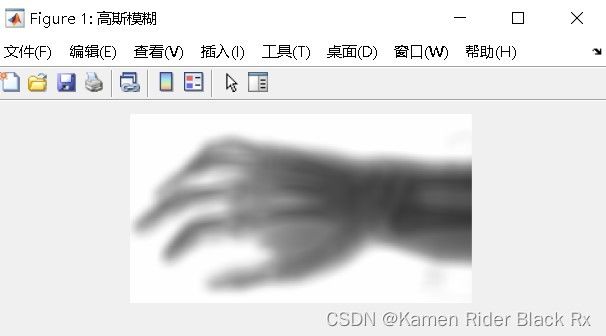
        5.USM虚光蒙版

 

图5-1 USM-原始图像

 

图5-2 USM-高斯模糊

 

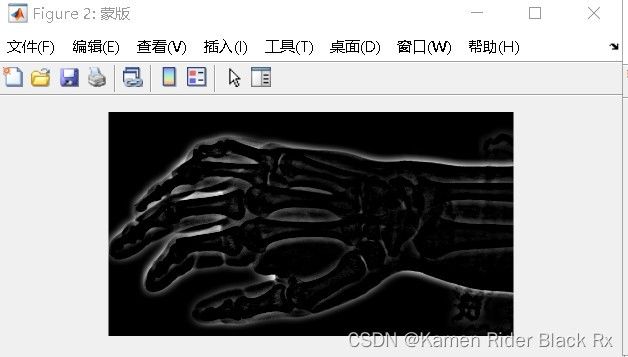
图5-3 USM-蒙版

        6.双边滤波

 

图6-1 噪声污染

 

图6-2 高斯滤波

 

 

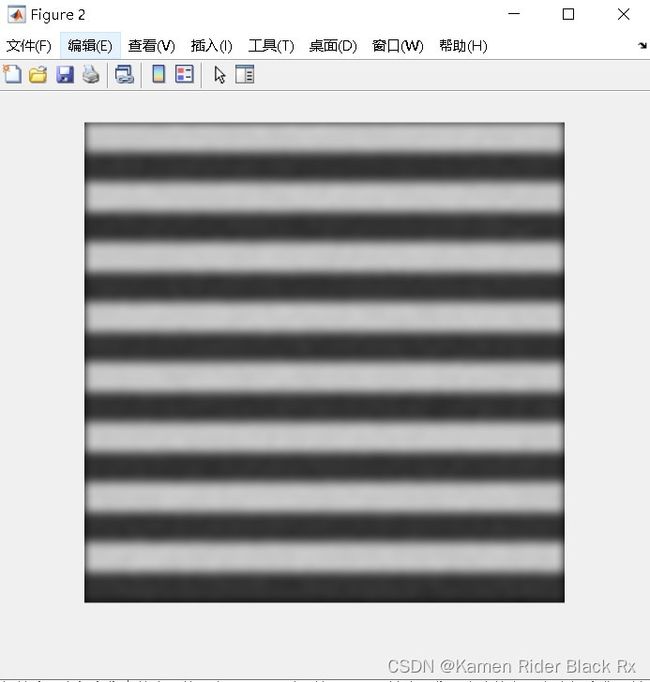
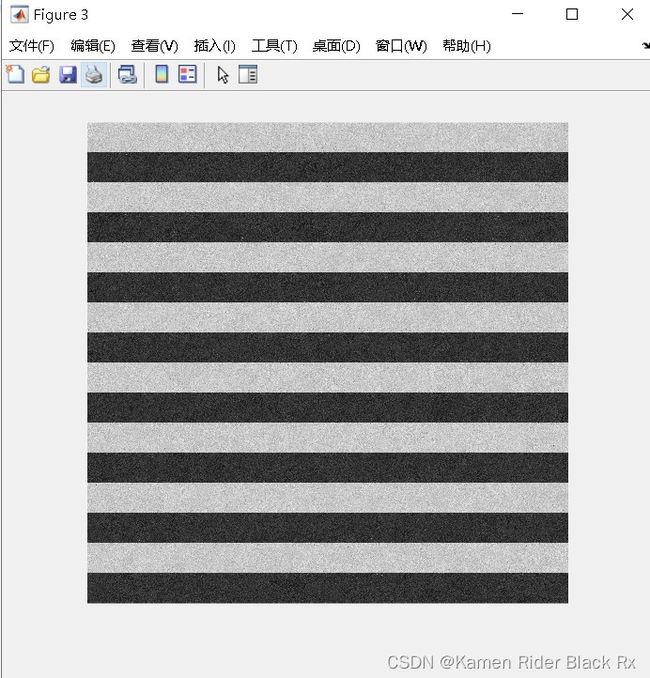
图6-3 双边滤波

• 实验心得：

在本次实验当中，我们学习了直方图均衡、分块直方图均衡、局部直方图均衡、局部增强、USM虚光蒙版以及双边滤波的实现方法。下面是对这些方法的原理的一些补充：

一、直方图均衡

直方图均衡化 (Histogram Equalization) 就是把一个已知灰度概率密度分布的图像经过一种变换，使之演变为一幅具有均匀灰度概率密度分布的新图像。过暗和过亮的图像 经过直方图均衡化，都可以使得图像变得清晰。

 

二、分块直方图均衡

针对传统的直方图均衡化算法易导致图像细节信息丢失和噪声放大的特点，分块直方图均衡在直方图均衡化算法的基础上加以改进，将图像的高频分量和低频分量分开进行处理,然后在进行合并，达到去噪的效果,能够在增强图像整体视觉效果的同时较好地保持图像细节,抑制图像噪声。

 

三、局部直方图均衡

局部直方图均衡算法

局部直方图均衡算法，又称为子块直方图均衡算法按 照所均衡子块的重叠程度来分类，可分为子块不重叠、子块 重叠与子块部分重叠三种，下面分别对它们作一简介：

子块不重叠的均衡算法

该算法将输入图像划分为一系列不重叠的子块，并对 每一个子块进行独立的直方图均衡其优点是图像局部细 节对比度能得到充分的增强，缺点是各子块的直方图均衡 函数差异较大，输出图像中难以避免块效应。

子块重叠的均衡算法

该算法 在输入图像上定义一个矩形子块，利用该 子块图像的直方图信息对子块中心的像素进行均衡将子 块中心逐像素移动并重复以上处理过程，直至遍历输入图 像的所有像素（方法类比于Niblack二值化的过程）。该方法不仅使图像局部细节得到充分的对 比度增强，同时消除了块效应由于子块均衡总次数等于输 入图像的像素总数，算法效率较低。

子块部分重叠的均衡算法

该方法（POSHE）与子块重叠方法的不同之处在于：

（1）子块不是逐像素移动，而是将 移动步长约取为子块尺 寸的几分之一。

（2）子块均衡的灰度转换函数不仅用于映 射子块中心像素灰度值，而且用于映射子块所有像素的灰 度值。

（3）对多次被均衡的像素，将均衡结果取平均作为该 像素在输出图像中的灰度值

 

四、局部增强

局部增强常用于一些要求特定增强效果的场合：

（1）局部增强可借助将图像分成子图像（一般奇x奇）再对每个子图像具体增强。

直方图变换是空域增强中最常采用的方法，它也很容易用于图像的局部增强。只需先将图像分成一系列（一般互相不重叠）小区域（子图像），此时直方图均衡化或规定化都可以基于小区域内的像素分布进行，从而使各小区域得到不同的增强效果。（对每个小区域进行全局增强）

（2）也可在对整幅图增强时直接利用局部信息以达到不同局部不同增强的目的。

 

1、m(x,y)和分别是以像素(x,y)为中心的邻域内的灰度均值和均方差值（标准差、是一个反差（对比的差异程度）的测度）。

2、M是f(x,y)的平均灰度值（即整幅图像的平均灰度，是一个平均亮度的测度）。

3、A（x, y）是一个放大倍数，k是一个比例常数。

4、f(x,y)减去m(x,y)是原始图与平均灰度的差异，然后将“差异”放大，最后将m(x,y)加回去是为了恢复原区域的平均灰度值。

5、其中越大的地方，灰度变化就越大，放大倍数越小；越小的地方，越平滑，增强效果放大。使得不同的地方采用不同的放大倍数，以像素为中心，与局部特征有关。（因为A（x, y）反比与均方差，所以在图像中对比度较小的区域得到的增益反而增大，这样就可以取得局部增强的效果。）

 

 

五、USM虚光蒙版

图象编辑过程中，可用的锐化工具很多，你可以为图象增加对比度、使用边缘锐化滤镜或噪音滤镜等，而虚光蒙版(USM)则是最成熟的锐化技术。虚光蒙版通过一个象素与一个象素相比较，对原图建立一个虚化版本，它增强了边缘的清晰度，却不会产生不自然的迹象，也不会消除低对比度区域的层次。

 

六、双边滤波

双边滤波(Bilateral Filters)是非常常用的一种滤波，它可以达到保持边缘、降噪平滑的效果。和其他滤波原理一样，双边滤波也是采用加权平均的方法，用周边像素亮度值的加权平均代表某个像素的强度，所用的加权平均基于高斯分布。最重要的是，双边滤波的权重不仅考虑了像素的欧氏距离（如普通的高斯低通滤波，只考虑了位置对中心像素的影响），还考虑了像素范围域中的辐射差异（例如卷积核中像素与中心像素之间相似程度、颜色强度，深度距离等）。