Neural Ordinary Differential Equations

Abstract

我们引入了一种新的深度神经网络模型家族。我们没有指定一个离散的隐藏层序列，而是使用神经网络参数化隐藏状态的导数。该网络的输出是用一个黑盒微分方程求解器来计算的。这些连续深度模型具有恒定的内存成本，可以根据每个输入调整其评估策略，并可以明确地用数值精度换取速度。我们在连续深度剩余网络和连续时间潜变量模型中证明了这些特性。我们还构造了连续的归一化流，一个生成模型，可以通过最大似然进行训练，而不需要对数据维进行划分或排序。对于训练，我们展示了如何通过任何ODE求解器可伸缩地反向传播，而不访问其内部操作。这允许在更大的模型中对ode进行端到端训练。

1 Introduction

残差网络、循环神经网络解码器和正则化流等模型通过组合一系列到隐藏状态的转换来构建复杂的转换：
$$h_{t+1}=h_t+f({\theta }_t,h_t)\text{\hspace{1em}(1)}$$其中$t\in \{1,...,T\},h_t\in {\mathbb{R}}^d$，这些迭代更新可以看作是一个连续变换的欧拉离散化。
当我们添加更多的图层和采取更小的步骤时，会发生什么？在极限情况下，我们使用一个由神经网络指定的常微分方程(ODE)来参数化隐藏单元的连续动态：
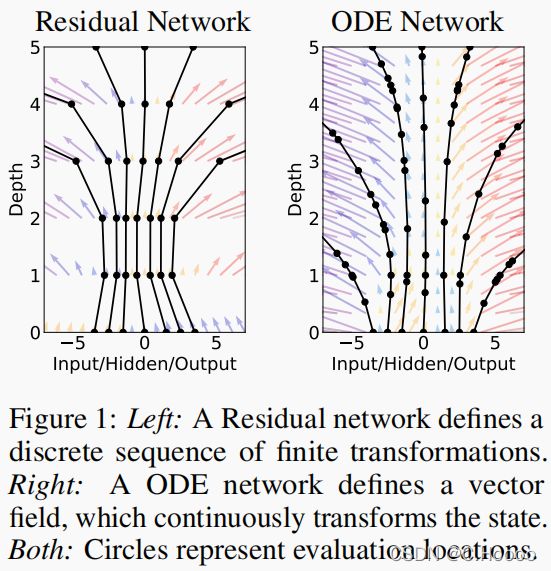
$$\frac{dh(t)}{dt}=f(h(t),t,\theta )\text{\hspace{1em}(2)}$$从输入层$h(0)$，我们可以定义输出层$h(T)$为在T时刻上ODE初值问题的解，这个值可以通过黑盒微分方程求解器计算，它评估隐藏神经元动力学f 在任何需要的地方求解符合精度要求的解。图1对比了这两种方法。

使用ODE求解器来定义和评估模型有几个好处：
Memory efficiency： 在第2节中，我们展示了如何计算关于任何ODE求解器的所有输入的标量值损失的梯度，而不通过求解器的操作反向传播。如果不存储任何中间数量的正向传递，我们就可以用恒定的内存成本作为深度的函数来训练我们的模型，这是训练深度模型的一个主要瓶颈。

Adaptive computation： 欧拉的方法可能是求解ode的最简单的方法。从那以后，高效和精确的ODE求解器已经发展了120多年。现代ODE求解器为近似误差的增长提供了保证，监测误差水平，并动态调整其评估策略，以达到所要求的精度水平。这使得评估模型的成本与问题的复杂性而变化。经过训练后，实时或低功耗应用程序的精度可以降低。

Scalable and invertible normalizing flows： 连续变换的一个意想不到的副作用是，变量公式的变化变得更容易计算。在第4节中，我们推导了这个结果，并利用它来构造一类新的可逆密度模型，它避免了规范化流的单个单元瓶颈，并且可以直接通过最大似然进行训练。

Continuous time-series models： 与需要离散观测和发射间隔的循环神经网络不同，连续定义的动态可以自然地合并在任意时间到达的数据。在第5节中，我们构建并演示了这样一个模型。

2 Reverse-mode automatic differentiation of ODE solutions(反向模式的自动微分ODE的解决方案)

训练连续深度网络的主要技术困难是通过ODE求解器执行反向模式微分（也称为反向传播）。通过前向传递的操作进行区分是很简单的，但会导致很高的内存成本，并引入额外的数值误差。

我们将ODE求解器视为一个黑盒子，并使用伴随灵敏度方法计算梯度(Pontryaginetal.，1962)。该方法通过求解第二个、增强了的时间向后（时间轴反向）的 ODE 来计算梯度，适用于所有的ODE求解器。这种方法与问题的大小成线性关系，内存成本低，并显式地控制数值误差。
考虑优化一个标量值损失函数$L()$，它的前向传播过程可以如下表示：

$z(t_1)$代表$t_1$时刻的隐藏状态，而当隐藏状态被连续化后，$t_0$到$t_1$时刻的中间隐藏状态的和就是等式中间部分的积分项。而整个前向过程可以用 ODE 求解器进行求解。

为了优化L，我们需要对θ求梯度。第一步就是要求L在每一个时刻对隐状态z(t)的梯度，这个量被称为伴随矩阵$a(t)=\partial L/\partial z(t)$。它的动态过程被另一个 ODE 来求解，可以把这种瞬时性被看作链式法则：
$$\frac{da(t)}{dt}=-a(t{)}^T\frac{\partial f(z(t),\theta ,t)}{\partial z}\text{\hspace{1em}(4)}$$这样, 再调一次求解器就可以解出$\partial L/\partial z(t_0)$。

这个求解器从初始值$\partial L/\partial z(t_1)$开始反向运行。一个复杂的问题是，解决这个ODE需要知道$z(t)$沿其整个轨迹的值。然而，我们可以简单地从最终值$z(t_1)$开始，将它的伴随$z(t)$一起反向重新计算。
计算关于参数θ的梯度需要计算第三个积分，它同时取决于z(t)和a(t)：

（4）和（5）中的$a(t{)}^T\frac{\partial f}{\partial z}$和$a(t{)}^T\frac{\partial f}{\partial \theta }$的vector-Jacobian products 都可以通过 ODE solver 快速求解， 所有的积分解z，a和$\partial L/\partial \theta$都可以通过一个 ODE solver 来求解，可以将它们组合成一个向量解 (增强的状态，augmented state)。算法1展示了如何构造必要的动态，并调用一个ODE求解器来一次计算所有的梯度。

大多数ODE求解器都可以选择多次输出状态z(t)。当损失依赖于这些中间状态时，反向偏导数必须被分解成一个单独的解序列，在每对连续的输出时间之间有一个解(图2)。在每次观测时，按相应的偏导数$\partial L/\partial z(t_i)$方向调整。

由损失敏感度$\frac{\partial L}{\partial z(t_N)}$调节伴随状态a(t)， 然后再有伴随状态 a(t) 得到损失敏感度$\frac{\partial L}{\partial z(t_N)}$。这是 ODE 反向的链式过程。至此，模拟了整个反向传播的过程

3 Replacing residual networks with ODEs for supervised learning

在本节中，我们将实验研究监督学习的神经ode的训练。

Software 为了从数值上解决ODE初值问题，我们使用了在LSODE和VODE中实现的隐式Adams方法，并通过scipy。集成包进行接口。作为一种隐式方法，它比龙格-库塔等显式方法有更好的保证，但需要在每一步都要求解一个非线性优化问题。这种设置使得通过集成器的直接反向传播变得困难。我们在Python的自动网格框架中实现了伴随灵敏度方法(Maclaurinetal.，2015)。在本节的实验中，我们使用张量流评估了GPU上的隐藏状态动力学及其导数，然后从FortranODE求解器中调用，从Python自动grad代码中调用。

Model Architectures 我们实验了一个小残差网络，该网络对输入进行两次降采样，然后应用6个标准残差块He等人(2016b)，它们被ODE-Net变体中的ODESolve模块所取代。我们还测试了一个具有相同架构的网络，但梯度直接通过龙格-库塔积分器反向传播，称为RK-Net。表1显示了测试误差、参数数量和内存成本。L表示ResNet中的层数，$L$是ODE求解器在单个向前传递中请求的函数计算数，可以解释为隐式的层数。我们发现ODE-Nets和RK-nets可以实现与ResNet几乎相同的性能。

Error Control in ODE-Nets ODE求解器可以近似地确保输出在真实解的给定容忍度范围内。更改此公差会改变网络的行为。我们首先验证了在图3a中确实可以控制错误。前向调用所花费的时间与函数评估的数量成正比(图3b)，因此调整公差给了我们一个在精度和计算成本之间的权衡。人们可以进行高精度的训练，但在测试时会切换到较低的精度。

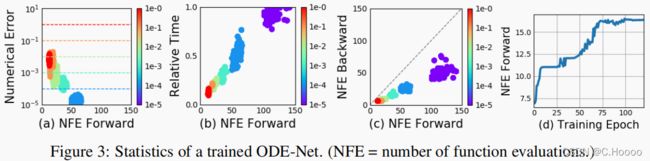
Network Depth目前尚不清楚如何定义ODE解决方案的“深度”。一个相关的数量是所需的隐藏状态动态计算的数量，这个细节委托给ODE求解器，并依赖于初始状态或输入。图3d显示，在整个训练过程中，功能评估的数量在训练过程中不断增加，这可能是为了适应模型不断增加的复杂性。

4 Continuous Normalizing Flows

离散化的方程（1）也出现在规范化流(Rezende和Mohamed，2015)和NICE框架(Dinh等人，2014)中。这些方法利用变量变化定理来计算样本通过双射函数$f$ 进行变换时概率的精确变化：$${\mathbf{z}}_1=f\left({\mathbf{z}}_0\right)⟹\log p\left({\mathbf{z}}_1\right)=\log p\left({\mathbf{z}}_0\right)-\log \left|\det \frac{\partial f}{\partial {\mathbf{z}}_0}\right|$$
经典的正则化流模型， planar normalization flows的公式如下:
$$\mathbf{z}(t+1)=\mathbf{z}(t)+uh\left(w^{\top }\mathbf{z}(t)+b\right),\log p(\mathbf{z}(t+1))=\log p(\mathbf{z}(t))-\log \left|1+u^{\top }\frac{\partial h}{\partial \mathbf{z}}\right|$$
使用变量代换公式的瓶颈是计算雅克比矩阵。它的计算复杂度要么是z维度的立方, 要么是隐藏单元数量的立方，最近的研究都是在NF模型的表达能力和计算复杂度做取舍。
令人惊讶的是，从一组离散的层移动到一个连续的变换，简化了规范化常数变化的计算。

定理1 变量瞬时变化定理
设$z(t)$ 是一个有限连续随机变量，概率$p(z(t))$ 依赖于时间. 则$\frac{dz}{dt}=f(z(t),t)$是$z(t)$ 随时间连续变化的微分方程，假设$f$ 关于z一致$Lipschitz$ 连续，关于$t$ 连续，那么对数概率密度的变化也遵循微分方程$$\frac{\partial \log p(\mathbf{z}(t))}{\partial t}=-\mathrm{tr}\left(\frac{df}{d\mathbf{z}(t)}\right)\text{\hspace{1em}(8)}$$
$proof$
为了证明这个定理，我们取了$logp(z(t))$ 随时间的有限变化的无穷小极限。首先，我们表示$z$ 对$\epsilon$ 的时间变化的变换为$$\mathbf{z}(t+ϵ)=T_{ϵ}(\mathbf{z}(t))\text{\hspace{1em}(14)}$$
我们假设$f$ 在$z(t)$ 上是Lipschitz连续的，在t上是连续的，因此每个初值问题通过皮卡德存在性定理都有一个唯一解。我们还假设$z(t)$ 是有界的。这些条件表明$f,T_{\epsilon }$ 和$\frac{\partial }{\partial z}{T}_{\epsilon }$ 都是有界的。在下面，我们使用这些条件来交换极限和乘积。

我们利用用变量的离散变化公式表示微分方程$\frac{\partial logp(z(t))}{\partial t}$，以及导数的定义：

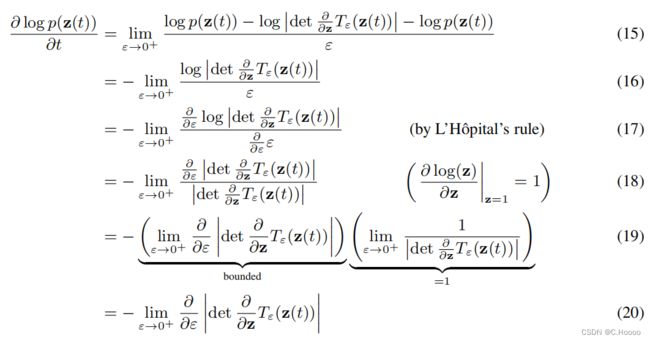
行列式的导数可以用雅可比公式表示，则有

行列式求导公式$$\frac{d|A|}{dt}=tr(A^{\ast }\frac{dA}{dt})$$

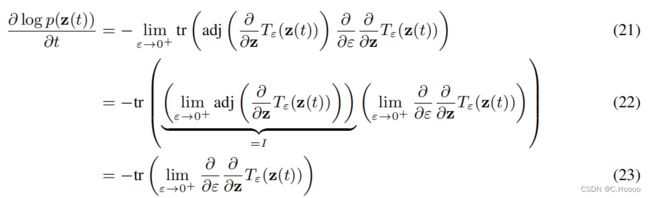用$T_{\epsilon }$的泰勒级数展开式代替$T_{\epsilon }$并取极限，完成了证明。

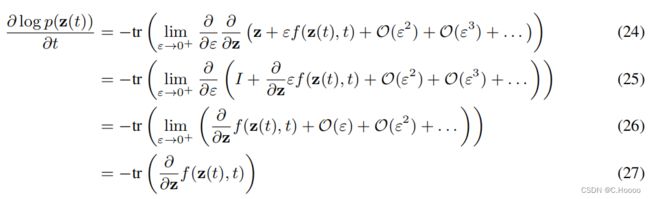
与(6)的$log$ 计算不同, 本式只需要计算迹(trace)的操作。另外, 不像标准的NF模型, 本式不要求f是可逆的, 因为如果满足唯一性，那么整个转换自然就是可逆的。

应用变量瞬时变化定理，我们可以看一下planar normalization flows的连续模拟版本：
$$\frac{d\mathbf{z}(t)}{dt}=uh\left(w^{\top }\mathbf{z}(t)+b\right),\frac{\partial \log p(\mathbf{z}(t))}{\partial t}=-u^{\top }\frac{\partial h}{\partial \mathbf{z}(t)}\text{\hspace{1em}(9)}$$
给定一个初始分布p(z(0))，我们可以从p(z(T))中采样，并通过求解这组ODE来评估其概率密度。

使用多个线性成本的隐藏单元

当det不是线性方程时, 迹的方程还是线性的, 并且满足$tr({\sum }_n{J}_n={\sum }_{n}tr(J_n))$ ，这样我们的方程就可以由一系列的求和得到, 概率密度的微分方程也是一个求和:
$$\frac{d\mathbf{z}(t)}{dt}=\sum _{n=1}^M{f}_n(\mathbf{z}(t)),\frac{d\log p(\mathbf{z}(t))}{dt}=\sum _{n=1}^M\mathrm{tr}\left(\frac{\partial f_n}{\partial \mathbf{z}}\right)\text{\hspace{1em}(10)}$$这意味着我们可以很简便的评估多隐藏单元的流模型，其成本仅与隐藏单元M的数量呈线性关系。使用标准的NF模型评估这种“宽”层的成本是$O(M^3)$，这意味着标准NF体系结构的多个层只使用单个隐藏单元.

依赖于时间的动态方程

我们可以将流的参数指定为t的函数，使微分方程$f(z(t),t)$随$t$ 而变化。这种参数化的方法是一种超网络. 我们还为每个隐藏层引入了门机制，$\frac{d\mathbf{z}}{dt}={\sum }_n{\sigma }_n(t)f_n(\mathbf{Z})$ ,${\sigma }_n(t)\in (0,1)$是一个神经网络, 可以学习到何时使用fn. 我们把该模型称之为连续正则化流(CNF, continuous normalizing flows)

4.1 CNF试验

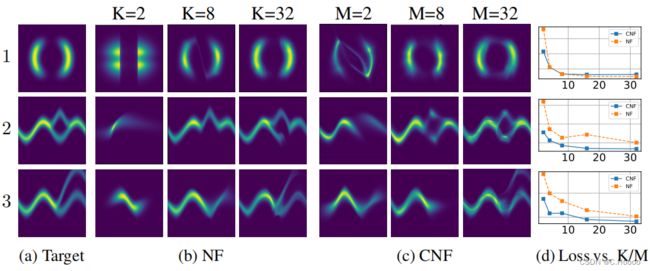
我们首先比较连续的和离散的planar规范化流在学习一个已知的分布样本。我们证明了一个具有M个隐藏单元的连续 planar CNF至少可以与一个具有K层(M = K)的离散 planar NF具有同样的拟合能力，某些情况下CNF的拟合能力甚至更强。

拟合概率密度
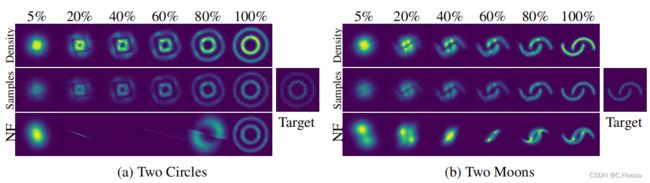
设置一个前述的CNF, 用adam优化器训练10000个step. 对应的NF使用RMSprop训练500000个step. 此任务中损失函数为$KL(q(x)||p(x))$ , 最小化这个损失函数, 来用$q(x)$ 拟合目标概率分布$p(x)$ . 图4表明, CNF可以得到更低的损失.

极大似然训练

CNF一个有用的特性是: 计算反向转换和正向的成本差不多, 这一点是NF模型做不到的. 这样在用CNF模型做概率密度估计任务时, 我们可以通过极大似然估计来进行训练 也就是最大化${\mathbb{E}}_{p(x)}[log(q(x))]$ ，其中$q$ 是变量代换之后的函数，然后反向转换CNF来从$q(x)$ 中进行采样

对于这个实验, 我们使用64个隐藏单元的CNF和64层的NF来进行对比，图5展示了最终的训练结果. 从最初的高斯分布, 到最终学到的分布, 每一个图代表时间t的某一步. 有趣的是: 为了拟合两个圆圈, CNF把planar 流 进行了旋转, 这样粒子会均分到两个圆中. 跟 CNF的平滑可解释相对的是, NF模型比较反直觉, 并且很难拟合双月牙的概率分布(见图5.b)