回溯法( Backtracking Algorithms ) :C语言Maze迷宫问题(自己实现)
http://www.cs.rpi.edu/~hollingd/psics/notes/backtracking.pdf
Two situations:
– Finding a solution to a problem can't be based on a straight path to the goal.
● consider traversing a maze.
– We need a better approach than brute force(independently evaluating all possible solutions).
● Think of the TSP problem – many possible solutions sharepartial tours (why not treat identical partial tours as a singlepartial solution?)
TSP:旅行推销员问题
http://en.wikipedia.org/wiki/Backtracking
http://baike.baidu.com/view/45.htm
自己实现的迷宫问题:
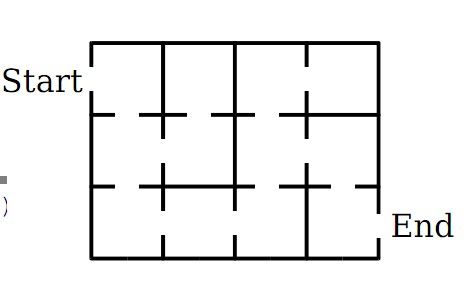
#include <stdio.h>
#include <stdlib.h>
#define true 1
#define false 0
typedef char byte;
typedef struct OneCell{
byte up;
byte down;
byte left;
byte right;
int step;
} Cell;
typedef struct Pos{
int x;
int y;
}Pos;
int Maze(Cell *pArr,Pos * pCurr, Pos * pDest, Pos * pSize ,int step){
Cell *pC = pArr + pCurr->x * pSize->y + pCurr->y ;
int cRow=pCurr->x;
int cCol=pCurr->y;
int eRow=pDest->x;
int eCol=pDest->y;
pC->step=step; //第几步
if(cRow==eRow && cCol==eCol){
int i=0,j=0;
printf("\nSuccess match!\n");
for(;i<pSize->x;++i){
for(j=0;j<pSize->y;++j){
printf("%4d",pArr[i*pSize->y+j].step);
}
printf("\n");
}
printf("Step=%d:[%d,%d]\n",pC->step,cRow,cCol);
return true;
}
if(pC->right==true && cCol<(pSize->y-1) && pArr[cRow*pSize->y + cCol+1].step == -1 ){
Pos pCurrNew;
pCurrNew.x=cRow;
pCurrNew.y=cCol+1;
if(Maze(pArr,&pCurrNew,pDest,pSize,step+1)==true){
printf("Step=%d:[%d,%d]\n",pC->step,cRow,cCol);
return true;
}
}
if(pC->down==true && cRow <(pSize->x-1) && pArr[(cRow+1)*pSize->y + cCol].step == -1){
Pos pCurrNew;
pCurrNew.x=cRow+1;
pCurrNew.y=cCol;
if(Maze(pArr,&pCurrNew,pDest,pSize,step+1)==true){
printf("Step=%d:[%d,%d]\n",pC->step,cRow,cCol);
return true;
}
}
if(pC->left==true && cCol>0 && pArr[cRow*pSize->y+cCol-1].step == -1 ){
Pos pCurrNew;
pCurrNew.x=cRow;
pCurrNew.y=cCol-1;
if(Maze(pArr,&pCurrNew,pDest,pSize,step+1)==true){
printf("Step=%d:[%d,%d]\n",pC->step,cRow,cCol);
return true;
}
}
if(pC->up==true && cRow>0 && pArr[(cRow-1)*pSize->y+cCol].step == -1 ){
Pos pCurrNew;
pCurrNew.x=cRow-1;
pCurrNew.y=cCol;
if(Maze(pArr,&pCurrNew,pDest,pSize, step+1)==true){
printf("Step=%d:[%d,%d]\n",pC->step,cRow,cCol);
return true;
}
}
pC->step=-1;
return false;
}
int main()
{
Cell cells[][4]=
{
{
{false,true,false, false,-1},
{false,true, false, false,-1},
{false,true, false, true,-1},
{false,false,true, false,-1}
},
{
{true,true,false,true,-1},
{true,false,true,false,-1},
{true, true,false,true,-1},
{false,true, true,false,-1}
},
{
{true ,false ,false ,true,-1},
{false,false,true ,true,-1},
{true ,false ,true,false,-1},
{true ,false ,true,true,-1}
}
};
//cells[0][0].step=0;
Pos pCurr={0,0},pDest={2,3},pSize={3,4}; // rows, cols
Maze((Cell *)cells,&pCurr,&pDest,&pSize,0 );
//true;
//printf("%d,%d,%d ",sizeof (Cell),false,c1.down );
return 0;
}
结果:
Success match! 0 -1 -1 -1 1 -1 5 6 2 3 4 7 Step=7:[2,3] Step=6:[1,3] Step=5:[1,2] Step=4:[2,2] Step=3:[2,1] Step=2:[2,0] Step=1:[1,0] Step=0:[0,0] Process returned 0 (0x0) execution time : 0.016 s Press any key to continue.