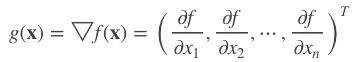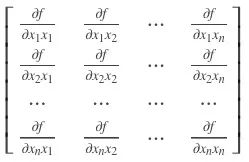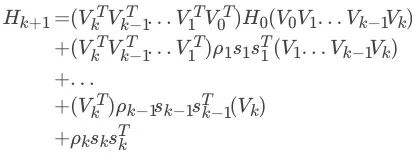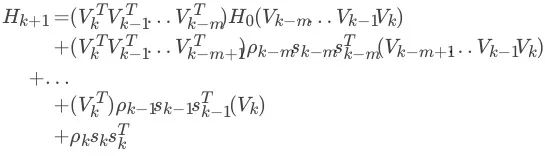二阶优化方法——牛顿法、拟牛顿法(BFGS、L-BFGS)
原文地址：二阶优化方法——牛顿法、拟牛顿法(BFGS、L-BFGS)
欢迎关注我的公众号，微信搜 algorithm_Tian 或者扫下面的二维码~
现在保持每周更新的频率，内容都是机器学习相关内容和读一些论文的笔记，欢迎一起讨论学习~
对于逻辑回归和最大熵模型等以似然函数为最优化目标的问题，一般常用的求解方法有梯度下降法、牛顿法和拟牛顿法等。梯度下降法是一阶优化方法。牛顿法和拟牛顿法是二阶优化方法。
牛顿法和拟牛顿法的优势是收敛速度快，但是牛顿法迭代的每一步都需要求解目标函数的二阶偏导矩阵——海森矩阵（Hessian matrix）的逆矩阵，计算较复杂。拟牛顿法简化了这一点，它通过正定矩阵近似海森矩阵或它的逆矩阵。
本篇博文就介绍二阶最优化方法中的牛顿法和拟牛顿法中的BFGS、LBFGS这几个方法。
1.牛顿法
2.拟牛顿法
2.1 BFGS
2.2 L-BFGS
1.牛顿法
假设存在一个无约束的最优化问题：最小化目标函数f(x)。
牛顿法就是利用迭代点
处的一阶导数（梯度）和二阶导（hessian矩阵）对目标函数进行二次函数近似，在每次迭代中迭代方向都是沿着当前点函数值下降的方向，不断重复这一过程直到求得满足精度的近似极小值。
假设f(x)有二阶连续偏导数，那么对它进行二阶泰勒展开有：
这里，
是f(x)在
的梯度向量：
是f(x)的hessian矩阵：
=
函数f(x)有极值的必要条件就是在极值点处一阶导数为0，即梯度向量为0。我们对 二阶近似 求导有：
那么极值点的求解为：
于是就有：
牛顿法算法步骤：
输入：目标函数f(x)，精度阈值
输出：使f(x)达到极小值的x
（1）初始化
，令k=0
（2）计算梯度
和hessian矩阵
（3）假如
，即在此点处梯度的值接近于0，则达到极值点处，停止迭代
（4）计算搜索方向
（5）计算迭代点
，
是步长
（6）令k=k+1，返回（2）
优点：收敛速度快
缺点：需要计算hessian矩阵或它的逆
2.拟牛顿法
牛顿法在每次迭代时都需要计算出Hessian矩阵或逆矩阵，非常耗时，并且Hessian矩阵可能难以甚至无法计算。于是拟牛顿法便被提出。它利用一个正定对称矩阵B来近似表示hessian矩阵或它的逆矩阵。
同上面
同上面一样，进行泰勒二阶展开求导后：
令
于是有
即
其中，
所以拟牛顿法模拟了牛顿法的方向。
上面的条件就被称为拟牛顿条件，用来近似代替hessian矩阵的矩阵就需要满足这个条件。
根据此条件的不同构造出了很多不同的拟牛顿法，下午是常用拟牛顿法的迭代公式：
2.1 BFGS
BFGS算法是它的四个发明人Broyden，Fletcher，Goldfarb和Shanno名字首字母的简写。算法的思想是构造Hessian矩阵的近似矩阵，相应的牛顿条件是：
相应的秩2近似为：
所以有：
其中，
于是上式变为：
对它的逆，则有：
BFGS算法流程：
输入：目标函数f(x)，精度阈值
输出：使f(x)达到极小值的x
（1）初始化，
令k=0
（2）计算梯度,假如，即在此点处梯度的值接近于0，则达到极值点处，停止迭代
（3）计算搜索方向
（4）一维搜索：求步长
使得
（5）计算迭代点
（6）计算
，假如
则停止计算，得到近似解x=
，计算
其中
（7）k=k+1，回到（3）
优点：
1、不用直接计算Hessian矩阵；
2、通过迭代的方式用一个近似矩阵代替Hessian矩阵的逆矩阵。
缺点：
1、矩阵存储量为n*n，因此维度很大时内存不可接受；
2、矩阵非稀疏会导致训练速度慢。
2.2 L-BFGS
BFGS每一步迭代需要计算nxn的矩阵B，当维度很大时非常耗费内存，所以提出了改进的L-BFGS方法，它只存储计算
需要的最近的m个
序列。
对BFGS有公式2.2.1：
令
，
（不代表hessian矩阵）表示
。则有：
那么通过递归迭代，可以得到：
然后为了算这个式子，需要不断迭代LBFGS原著中给了一个两层的递推（two-loop）程序求这个式子，只保留最近m步：
更新方向：
在L-BFGS中的two-loop计算更新方向的步骤：
参考资料：
【1】李航，统计学习方法
【2】https://en.wikipedia.org/wiki/Limited-memory_BFGS
【3】https://en.wikipedia.org/wiki/Newton%27s_method_in_optimization
【4】https://zh.wikipedia.org/wiki/%E7%89%9B%E9%A1%BF%E6%B3%95
【5】https://blog.csdn.net/lansatiankongxxc/article/details/45873597
【6】https://zhuanlan.zhihu.com/p/37588590
【7】 https://www.cnblogs.com/vivounicorn/archive/2012/06/25/2561071.html
牛顿法和拟牛顿法的介绍到这里就结束啦。
下次博文准备介绍加入L1正则项的拟牛顿法：OWL-QN算法。
欢迎大家留言讨论~
欢迎扫描或长按二维码关注我
每周一篇技术分享
