上市公司风险预警案例可视化演示系统（附代码）

摘要

上市公司作为我国企业中的特殊群体和证券市场的基石，其经营质量和经营业绩的优劣直接影响证券市场的建设和发展，进而间接影响着我国国民经济体系的稳定和健康发展。随着我国经济的快速发展，财务风险对上市公司造成的危害程度正在日益加深，它不仅影响企业的生存和发展，而且也给相关利益者带来巨大损失。因此如何从企业经营过程产生的大量财务数据中挖掘出对企业财务风险有预警作用的信息成为我国上市公司迫切需要解决的问题。而数据挖掘技术的不断成熟正好解决了这一问题。数据挖掘具有通过对大量历史数据分析，挖掘出潜在的规则和知识的功能。因此运用数据挖掘技术对我国上市公司财务风险预警进行研究，构建一个有效适用的财务风险预警模型，具有十分重要的理论意义和现实意义。
本文主要研究数据挖掘中Logistic回归、神经网络和决策树在上市公司财务风险预警中的具体应用。首先本文介绍了财务风险预警和数据挖掘技术相关理论；其次介绍了财务风险预警模型研究流程，并详细阐述了本文所用的三种数据挖掘技术；然后结合我国上市公司实际情况，构建了财务风险预警指标体系；最后以2005-2007年77家首次被ST处理的制造业上市公司及其配对公司为研究样本，以被ST处理前第2-4年的财务数据为基础，以CRISP-DM数据挖掘流程模型为框架，运用CLementine数据挖掘工具实现了数据挖掘技术在财务风险预警中的应用。
本文研究发现，运用数据挖掘技术建立的财务风险预警模型具有很强预警能力。从三个模型预测能力看，距离ST的时间越近，预测准确率越高；从短期预警看，三种模型都较好的预测效果，但是从长期预警看，神经网络和决策树的预测效果要优于统计分析的Logistic 回归；基于知识发现类的数据挖掘技术不但适合应用于短期预警，也适合应用于较长时期预警。因此数据挖掘完全可以应用到财务风险预警分析中，以达到运用数据挖掘技术进行决策支持的目的。
**关键词：**风险预警；数据挖掘; logistic回归; 神经

第一章 引言

1.1 研究背景

竞争激烈的市场经济一方面为企业提供了广阔的经营舞台，一方面暗藏了无数激流和险滩，稍有不慎就可能被卷入失败的漩涡。国内外大量的实例表明，陷入经营危机的企业几乎毫无例外的都是以出现财务危机为征兆。企业发生财务危机的原因可能是多方面的，既有可能是外部原因，如战争、经济衰退、通货膨胀等，也有可能是内部原因，如企业经营者决策失误、管理失控等，或者是其他的一些特殊原因。但大多数企业的财务危机都有一个逐步显现不断悲化的过程。因此，应对企业的财务运营过程进行跟踪、监控，及早发现财务危机信号，预测企业的财务危机，使企业能够及时应变，避免或减少企业卷入危机。无论对经营者、投资者、债权人、政府或其他相关利益主体来说，建立财务预警系统，对企业财务状况进行预测都具有非常重要的现实意义。而另外从宏观经济运行的角度而言，自从1997年东南亚引发金融危机并迅速波及到全球以来，人们开始反思探讨造成危机的根源。各项研究表明，除了经济、金融体制和腐败等深层次原因外，引发危机的另一个重要原因就是相关的经济信息不全，缺乏必要的监测和预警机制。因此就经济运行的角度而言，建立一个功能强大的、可操作性强的危机监测预警系统十分必要。
当前，证监会加强了对上市公司的监管力度。自1986年我国通过了《破产法》以来，破产企业的数目逐年增加。我国很多企业都面临着企业失败或破产的问题。
1994年7月1日正式实行的《公司法》157条规定：“上市公司如果在最近三年连续亏损，由国务院证券管理部门决定暂停其股票上市”第158条规定：上述倩形在期限内未能消除，由国务院证券管理部门决定终l：其股票上市”。随后，中国证监会于1998年3月16日正式公布了《上市公司状况异常期间的特别处理》的规定，其中规定“当上市公司出现财务状况或其它状况异常，导致投资者对该公司前景难以判断，可能损害投资者权益的情形，交易所将对其股票交易实行特别处理”。
中国资本市场在十儿年中获得巨大的发展。股票市场对国有企业转换经营机制、建立现代企业制度产生了有力的推动作用。因此上市公司财务状况好坏影响巨大，且无疑是非常引人注目的。目前一项科研成果揭示出令人担忧的现状：用国际通用会计准则衡量，我国80%以上的上市公司存在财务隐患]。根据中国国情大幅度降低评价标准后，仍有将近20%的上市公司存在较为严重的财务问题。我国上市公司的平均资产负债率、平均的长期资金适合率、应收账款增长率与主营业务增长率之比等，都远远高于国际标准。
由于目前中国证券市场己经逐步完善了对经营管理不善上市公司的退出机制，对于上市公司而言，如何在财务危机到来之前就预先觉察其苗头，并提前告知管理者、投资者及其他相关利益主体，以便尽早采取措施，消除危机隐患，己成为当前有待解决的现实问题。
1.2 研究意义
正是基于上述背景，建立上市公司财务预警系统对各个相关利益方面都具有重要意义：
①对投资者：个人投资者中占大多数的中小投资者无论是从资金量的拥有还是对信息的获取角度来看，都属丁弱势群体。借助于上市公司的财务预警系统，中小投资者能够从盲目跟庄的风气中解脱围来，将有助于他们树立正确的投资理念。中小投资者通过上市公司预警系统能较为容易地判断上市公司的经营状况，推断出哪些公司将滑向ST、暂停上市，甚至退出证券市场。这为他们做出正确的投资决策提供了有益的帮助。这在当前大力提倡保护中小投资者利益的中国证券市场上有重要的现实意义。而对于机构投资者而言，也需要一种能够客观评判上市公司经营状况的预警系统。如今的中国证券市场正在提倡“超常规发展机构投资者”，希望借助机构投资者的一些先进的投资理念，来扭转当前证券市场上弥漫着的投资气氛。机构投资者作为一个独立的经营实体，也面临着为他们所管理的资产组合如何选股的问题。借助上市公司的财务预警系统，机构投资者可以很容易地评判出不同股票之间的优劣，为他们的最终选择提供技术支持。
②对上市公司管理层：上市公司管理层希望及时发现公司经营状况的恶化，以及是何种原因导致公司的财务状况出现恶化，从而能够及时地，有针对性地调整公司的经营方针，来扭转公司经营状况恶化的趋势。上市公司预警系统正是能够为上市公司管理层提供上述信息的有效手段。从企业管理者的角度而言，一个有效的财务预警系统具有以下职能：
1）收集信息。通过收集与企业有关的国家产业政策、竞争者的状况、企业自身的财务及经营状况资料、向预警系统提供全面、准确、及时的信息，做好财务预警的前期准备工作。
2）预防财务危机发生。通过对大量信息的分析，当企业可能发生财务危机的征兆出现时，财务预警系统能预先发出警告，提醒经营者、投资者等相关利益方早做准各，采取对策应变，避免潜在风险演变成现实的损失。
3）控制财务危机的进一步扩大。当财务危机的征兆出现时，有效的财务预警系统不仅能预知并预告财务危机，还能及时找出导致企业财务状况恶化的症结所在，以便有关各方对症下药，阻化财务状况的进一步恶化。
4）避免类似财务危机的再次发生。有效的财务预警系统不仪能及时避免现存的财务危机，而且能通过系统详细记录财务危机发生的原因、解决措施、处理结果，有关各方可以财务预警系统提供的这些资料为依据，总结经验教训，避免类似财务危机的再次发生。
应该注意的是，企业财务预警系统是企业预警系统的一部分，它除了能够预先告知经营者、投资者企业组织内部财务运营体系隐藏的问题之外，还能清楚的告知企业经营者应朝哪个方向努力米解决问题。
③对证券监管部门：建立套有效的上市公司财务预警系统，有利于证券监管部门因势利导，制定切实可行的监管政策，对证券市场实施有效监管，更好地推动中国证券市场的健康发展。
1.3 研究思路
本文尝试用组合预测方法构建财务危机预警模型，以期能提高预测的精度，使之成为预测上市公司财务危机状态的有效工具。本文的研究思路如下：
①回顾国内外财务预警模型研究文献；
②界定财务危机概念；
③建立财务预警指标体系；
④提出组合预测方法；构建基于BP神经网络的财务危机组合预警模型；
⑤实证研究；
⑥结论与建议。
本文研究的主要目的是力图建立一种较为优化的对公司财务状况进行预警的模型。本文一共使用了三种预测模型，先使用Z分数判别模型和Logistic回归分析模型从不同角度对公司的财务指标进行分析，得出两种预测数据。然后把这两个预测数据作为输入变量，经过BP神经网络模型的处理，把这两种预测结果进行非线性组合，以期得到较优的预测结果。

第二章 财务危机预警的理论基础

2.1 财务危机
财务危机（Financial Crisis），又称财务困境（Financial Distress）、财务失败（Financid Failure）。从严格意义上讲，严重的财务危机是财务失败或破产。
关于财务危机的定义和财务危机企业的界定，国内外学术界有不同的观点。
1972年，Camichael给财务危机下的定义是：企业履行义务时受阻，具体表现为：流动性不足、权益不足、债务拖欠、资金不足。
同年，Deakin认为财务危机是：己经经历破产、无力偿债或为债权人利益而已经进行清算的状态。
1986年，Foster对财务危机的认识是：除非对经济实体的经营或结构实行大规模重组否则就无法解决的严重变现问题。
1999年，Ross从四个方面界定财务失败：企业失败、法定破产、技术破产、会计破产。
1999年，国内学者谷棋、刘淑莲给财务危机下的定义是：企业无力支付到期债务与费用的一种经济现象，包括资金管理技术性失败直致破产。
综上所述，本文倾向于将财务危机定义为一个企业的现金流不足以支付企业的到期债务，包括借款和各种应付款。从这个角度看，陷入财务危机的企业既可能是亏损企业，也可能是盈利企业。企业在通过并购等一系列手段快速发展时，往往容易忽略企业财务风险，如盲目投资导致大量现金流出，所投项目可能不是公司擅长的领域导致未来经营收益很不确定，以及企业由于自身管理不当导致负债结构不合适，或应收账款占流动资产比率过高等，存在这些问题就很容易陷入财务危机。
2.2 预警理论
预警原义是指在敌人进攻之前发田警报，以做好防守应战的准备。19世纪末，人们开始把预警思想应用于经济领域，但主要是对宏观经济的预测与警示，以显示一个国家经济运行过热或过冷的不良状态。直到20世纪60年代，欧美一些国家才开始将预警思想运用于微观经济领域，对企业的经营状况进行事前监测，以便在企业经营出现危情之前，发出警告，采取措施加以排除。
2.2.1 企业预警理论
企业预警理论是一门专门揭示企业经营活动中的逆境现象：企业逆境、管理波动、管理失误、管理失误行为等的本质特征、成因机理和发生规律，研究如何构建企业管理系统的防错、纠错机制及建立避防失误、扣转逆境的管理系统的基本理论企业预警理论主要包括企业逆境管理理论、企业生命周期理论和企业诊断理论。
①企业逆境管理理论
企业逆境，是指由于环境的突变或内部管理不良，使企业经营陷入极端窘困的一种状态。它的现实特征有三：一是企业经济活动遭受严重的、连续的挫折与损失；二是出现经营亏损或亏损趋势（如企业的市场份额大幅度减少，产品质量急剧下降，即使暂时没有亏损，但其非常状态表明企业正在遭受并将继续遭受挫折，使亏损的发生不可避免）；三是出现资不抵债的危机现象。这三种现象中的任何一种，都足以说明企业陷入逆境。三种现象互相联系，呈现直接的因果关系。它们都有一个重要的识别特征：一旦逆境发生便难以在短期内迅速扭转。企业逆境现象是客观的，也是普遍的，但也是可以认识、预防和避免的。企业逆境管理理论，就是要研究企业经营失利、管理失误的成因机理和运动规律，研究防止和摆脱企业逆境、保持顺境的管理方法理论。
②企业生命周期理论
企业生命周期理论是20世纪90年代以来国际上流行的一种管理理论，它以研究企业成长阶段模型为核心内容。这种理论的核心观点是：企业像生物有机体一样也有一个从生到死、由盛到衰的过程。企业生命周期一般可分为孕育期、生存期、成长期、成熟期、衰退期和蜕变期。各阶段的主要特征如表2.1所示。
表2.1 企业各成长阶段的主要特征

企业的每个成长阶段都是山前期的演进和后期的变革或危机组成，变革的顺利与否直接关系到企业的持续成长问题；而危机稍有处理不当，就会对企业的生存造成威胁，甚至走向灭亡。因此，在每个成长阶段企业都会面临健康成长和经营失败两种选择。企业生命周期理论揭示了企业在其内在动力的推动下，如何发展变化，并对生命周期中的每个阶段可能发生的“病症”做出预测和解释，并同时给出诊断方法。
③企业诊断理论
企业诊断理论（Management Diagnosis）产生于20世纪30年代的美国，至今已经形成了一套较为成熟的企业诊断理论与方法体系。企业诊断，仍以一般意义的企业管理原理、原则为理论依据，采用有利于诊断功能的独特分析模式和技术方法，对企业各个方面进行诊断，主要包括以下内容：经营诊断（经营战略、市场营销、经济活动分析）、生产诊断（现场管理、质量管理、设备管理等）、组织诊断（组织结构、组织冲突、信息沟通等）和技术诊断（纯粹的工程或技术问题），从而帮助企业发现或判断企业管理中存在的主要问题，确诊产生问题的原因，提出改进企业管理水平的方案。
2.2.2 财务危机预警理论
企业财务预警系统是指为了防止企业财务系统运行偏离预期目标而建立的报警系统。从该定义中可以看出，财务预警系统不仅仅只是针对财务危机的预警或者说是只有当企业财务将要发生危机的时候才进行的预警，而是只要企业财务系统运行偏离预期的目标就要报警]。
企业财务预警系统具有下面的特性：一是针对性。根据企业发展规律和结构特点，从众多指标中选出能灵敏、准确反映出企业财务风险发展变化的指标及指标体系，反映企业发展中所处的财务状态，为决策者和投资着提供决策支持。二是预测性。企业财务预警系统要能预测企业财务状况的发展趋势和变化，可以为科学决策提供依据，能尽量减少决策者的失误。
目前，对于财务危机预警的研究，无论在国际还是国内都是一个正在探索的课题。因此其理论发展尚处于一种前沿性和创新性的研究阶段，并没有完备的理论。目前国内外学者对财务危机预警的研究主要有：混沌理论（Chaos）和灾害理论（Catastrophe）。主要用外米冲击来解释公司破产。其次是契约理论的代理模型（Agency model），认为公司变现价值和账面价值之比对公司投资行为有很大的影响，同时债务的期限结构也是影响投资效率的显著因素；认为短期银行借款在总负债中的比率越高，企业的投资效率也越高，这是因为银行相对丁其他债权人来说，更具有信息优势和谈判能力，更能保护所有债权人和股东的共同利益。另外许多管理学领域的学者将管理失误作为公司经营失败的主要原因，如权力过于集中、缺乏内部控制机制或机制没有得到有效的执行、会计及财务控制不严、对竞争反应太慢、经营缺乏多元化、借贷过渡等等。
财务危机预警作为预警管理理论体系的重要组成部分，其在研究思路、研究方法等方面，厂必然要遵循、借鉴经济、企业预警管理理论。预警管理理论对财务危机预警的指导是直接的、重要的，它是财务预警研究的论基础。

第三章 预警指标体系的建立

3.1 财务危机预警样本指标的选取
美国纽约大学的Edward·Altman教授在建立企业破产预测的Zeta模型时，财务指标的最初选取遵循了两个原则：一是该指标在以前的研究中出现的频率；二是指标与所要研究问题的潜在相关性。本文预警指标的选取在此基础上，另外还考虑了以下几个原则：
①灵敏性原则
所选取指标对经营危机的情况能准确、科学及时的反映，成为企业经营状况的睛雨表。灵敏性是指被选择的财务指标要能够比较灵敏地反映财务运行的主要方面。并及时再现财务管理的真实状态。
②可比性原则
所选取指标应根据我国日前通用的公司财务报表为基础设置指标，且指标不但能够反映公司的危机状况，且具有经济意义。要充分的考虑指标的可比性，舍去不具有普遍意义的指标。
③针对性原则
指指标与危机的生成过程密切相关。就财务层面上看，诱发财务危机最为直接的原因，可能是由于资源配置缺乏效率或对竞争应对不当，导致了企业在竞争中处于劣势地位，未来现金流入能力低下；也可能是企业一味地追求销售数额的增长，却忽略了对销售质量一现金流入的有效支持程度及其稳定可靠性与时间分布结构等的关注，由此导致企业陷入了过渡经营状态与现金支付能力匮乏的困境。这就要求预警指标应当依托这些根源加以把握从财务危机的根源选择指标。
④可操作性原则
指根据现有公开的财务会计信息，能够直接或间接地得到各有关的指标。因为要体现上述原则的指标数不胜数，但有些指标的数据很难取得，需要耗费大量的人力和物力，因此这些取得成本很高的指标将不予以考虑。
⑤系统性原则
指标体系的构建应有高度的概括性和覆盖面，能比较完整、全面、真实地反映预警管理的实际效果以及存在的问题。且各指标都能单独体现某一预警含义，而整体指标体系可以综合地反映企业财务管理的总体状态。
3.2 财务危机预警指标体系
根据以上原则，本文在借鉴国内外学者的实证研究成果并结合我国上市公司实际情况的基础上，从表内信息和表外信息两个角度六个方面25个财务指标构建上市公司财务危机预警的指标体系，作为研究中使用的初始变量。
①表内信息指标
表内信息指标主要包括反映企业盈利能力、经营能力、偿债能力、成长能力和现金流量五个方面的财务指标，具体说明如下。
1）盈利能力指标
盈利能力是指上市公司赚取利润的能力，也是上市公司财务结构和经营绩效的综合体现。其盈利能力大，在获取贷款、增资扩容方面就有优势；盈利能力小，其发行的股票就难有市场。该类指标通常越高越好。
a.净资产收益率
净资产收益率反映所有者投资的获利能力。净资产收益率越高，说明所有者投资带来的收益越高。净资产收益率是从所有者角度考察企业益利水平的高低，该指标越高，反映单位资产创造的利润越大，说明资产增值能力强，充满活力和生机，企业财务状况比较健康。
b.总资产报酬率
总资产报酬率反映企业总资产获得利润的能力，是反映企业资产综合利用效果的指标。该指标越高，表明资产利用效果越好，整个企业的活力能力越强，经营管理水平越高，发生财务危机的可能性越小。
c.每股收益
每股收益表明普通股每股分得的利润，反映了公司分配股利的能力。每股收益越大，企业越有能力发放股利，从而使投资者得到回报。股东对企业充满信心，财务安全。
d.主营业务利润率
主营业务利润率反映主营业务收入带来净利润的能力，主营业务是上市公司的核心业务，是上市公司重点发展方向和利润的主要来源。这个指标越高，说明企业每一元的主营业务收入所能创造的利润越高，主营业务的盈利能力就越强。
e.成本费用利润率
成本费用利润率表示企业为取得利润而付出的代价，从企业支出方面评价企业的获利能力，有利于促进企业加强内部管理，节约支出，提高经营效益。该指标越高，说明企业投入产出比越高，单位成本费用创造的利润越大，企业财务状况越健康。
2）营运能力指标
资产的营运能力反映企业资产的利用状况，它与企业的财务状况密切相关。这类指标也是越高越好。
a.总资产周转率
总资产周转率反映企业总资产的周转速度或企业的营运能力。比率越高，说明企业资产的周转速度越快，利用效果越好，企业发生财务危机的可能性；反之，说明企业资产的周转速度慢，发生财务危机的可能性大。
b.应收账款周转率
此项指标反映了应收账款流动程度的大小及应收账款管理效率的高低，周转率越高，表明企业收帐迅速，账龄期限较短，资产流动性大，短期偿债能力强。
c.存货周转率
此项指标不仅反映企业采购、储存、生产、销售各环节管理状况的好坏，而且对企业的偿债能力及获利能力产生决定性的影响。一般来说，存货周转率越高，表明其变现速度越快，资产占用水平越低，成本费用越节约。此指标还在一定程度上反映企业资产流动性的强弱。
3）偿债能力指标
偿债能力是指企业在一定期间内清偿到期债务的能力，对于大多数上市公司而言，资金米源除了股东权益外，还有相当一部分来自对外负债。偿债能力的强弱是衡量上市公司经营绩效的重要指标，也与公司的筹资能力息息相关，关系到市公司是否因财务状况异常被特别处理。
a资产负债率
资产负债率又称财务杠杆系数，该指标反映了企业总资产来源于债权人提供的资金的比重，以及企业资产对债权人权益的保障程度。在生产经营状况良好的情况下，可以利用财务杠杆的正面作用，得到更多的经营利润。如果企业的经营状况不佳，不但企业资金实力不能保证偿债的安全，财务杠杆还会发挥负面作用导致财务状况越加恶化。
b流动比率
流动比率表示企业每一元流动负债有多少流动资产作为偿还的保证，反映企业用一年内变现的流动资产偿还流动负债的能力。该指标值越大，企业短期偿债能力越强，企业因无法偿还到期的流动负债而产生的财务风险越小。
C.速动比率
流动资产中的存货可能由于积压过久等原因无法变现或者变现价值远远低于账面价值；待摊费用一般也不会产生现金流入。因此，仅以流动资产中变现能力最强的部分与流动负债的比值计算得出速动比率。速动比率越高，表明企业未来的偿债能力越有保证，发生财务危机的可能性越小。
d.营运资本比率
营运资本是流动资产与流动负债的差额，它是企业开展日常生产经营活动的资金保证，它的数量决定着企业资金的整体平衡情况，对企业的短期偿债能力产生很大影响。一般情况下，该比率越高，企业的破产风险越小，陷入财务危机的可能性也越小。
4）成长能力指标
成长能力是指上市公司通过自身的生产经营活动不断发展的能力。成长能力反映了上市公司的发展潜力，该类指标越大越好。
a主营业务收入增长率
主营业务收入增长率反映了公司主营业务收入规模的扩张情况，即反映了公司产品的市场大小。一个成长性的企业，这个指标的数值通常较大。处于成熟期的企业，这个指标可能较低，但是凭借已经占领的强大的市场份额，也能够保持稳定而丰厚的利润。处于衰退阶段的企业，这个指标甚至可能为负数。这种情况通常是危机信号的征兆。
b.净利润增长率
净利润增长率指标反映企业获利情况的增长情况，反映了企业长期的盈利能力趋势。上市公司的积累、发展以及投资者的回报，主要取决于净利润的增加。该指标是从资产增量扩张方面衡量发展能力。
c.总资产增长率
总资产增长率衡量上市公司本期资产规模的增长情况，评价经营规模总量上的扩张程度。总资产增长率指标是从资产总量扩张方面衡量发展能力，表明规模增长水平对发展后劲的影响。该指标越高，表明一个经营周期内资产规模扩张的速度越快。但实际操作时，应注意资产规模扩张的质与量的关系，以及企业的后续发展能力，避免资产盲日扩张。该指标是考核企业发展能力的重要指标。
d.每股收益增长率
每股收益增长率反映普通股每股盈余的增长情况，表明主市公司发放股利的实力扩张状况。该指标越高，股东对公司越有信心，公司的发展环境越好，发生财务危机的可能性越小。该指标是衡量上市公司成长能力的特有指标。
5）现金流量指标
现金流量是企业的生命。一个企业的偿债能力取决于企业在特定时点的现金流量，未来发展能力取决于企业长期稳定的现金流量，而不是企业净利润的多少。企业一切的经营活动不是为了获得利润，而是要为企业带来持续不断的现金流入，净利润只不过是会计账簿上的一堆数字，其能否转化为现金还有待确定。其次，在中国盈余操纵现象严重、会计信息失真的现实下，现金流量数据较之会计数据有更佳的可信性（当然也不能排除现金数据造假的可能性）。
a现金流动负债比
此指标从现金流量方面衡量企业短期偿债能力，能准确反映企业当期经营活动现金净流量和短期优先债务的比值，体现企业的支付能力。该指标越大越好。
b.净收益营运指数
该指标表明每一元净利润中经营活动产生的现金净流入，反映企业净利润的收现水平。一般来说，该指标越高越好，表明企业实现的净利润中流入现金的净利越多，可供企业自由支配的货币资金增加量越大，有助于提高企业的偿债能力和付现能力。
c.销售现金比率
该比率反映每元销售收入得到的净现金，同净收益营运指数指标一样反映了企业的收现能力，其越大越好。
d.每股营业现金流量
该指标反映了公司在维持期初现金存量的条件下，有能力发给股东的最高现金股利，更有利于投资者对企业的股利发放能力进行客观评价。
②表外信息指标
从目前的研究成果看，选择的定量指标通常是财务信息。但是通过对大量的出现财务危机状况的公司的研究发现，有时非财务信息（表外信息）比如上市公司过度依赖短期借款、存在大量的或有事项（主要是因担保、财务承诺而产生的或有负债）、审计报告的意见类型、期末存在大量关联方交易等更能揭示公司陷入财务危机的状况。因此本文把这类非财务信息引入到预警指标体系，这是以往研究中忽视的地方。
1）短期借款流动比率
对于止市公司过渡依赖短期借款这指标，采用短期借款流动比卒来衡量。当上市公司开始出现应付款项不能偿还时，往往依赖短期借款来进行周转。因此当这一指标明显升高时，就有可能是市公司出现偿付危机，流动资金周转困难的征兆。
2）或有负债总资产比
上市公司由于担保、财务承诺、违约以及财产诉讼等原因可能产生或有负债。
由于或有负债的发生是不可预期的，有时甚至超过公司净资产，出现资不抵债的情形，持续经营受到威胁。或有负债总资产比可以衡量公司出现或有事项的危机程度，这个指标越低越好。
3）关联交易比率
当上市公司出现严重亏损，陷入危机时，往往通过期末大量的关联交易粉饰报表，以达到掩人耳目的目的。因此当期末出现大比数额的关联交易时，往往是上市公司出现财务危机的预兆。
4）审计意见类型：分为无保留意见、保留意见、无法表示意见或否定意见3种。
当上市公司出现财务危机时，为了掩人耳目，有可能在报表上编制虚假信息，此时注册会计师进行审计时就有可能发现问题，出示否定意见或无法表示意见的审计报告。因此审计报告的意见类型在一定程度上也是上市公司陷入财务危机的征兆。
表3.1 财务危机预警指标列表

第四章 财务危机预警模型的构建

4.1 传统财务危机预警方法评析
4.1.1 传统财务危机预警方法回顾
①定性预警模式
定性预警分析己有的并广为接受的方法主要包括以下几种方法。
1）标准化调查法
标准化调查法又称风险分析调查法，即通过专业人员、咨询公司等，就企业可能遇到的问题加以详细的调查和分析，形成报告文件供企业经营者参考的方法。此时这些标准化的问题就是财务预警的指标即警素，警兆即体现在企业对问题的回答中。这种方法的主要缺点是对特定企业来说无法提供特定问题，无法发现一些企业的个性特征。
2）“四阶段症状”分析法
该方法认为企业财务运营情况不住肯定有特定的症状，而且是逐渐加剧的，因此把企业财务运营“病症”大体分为四个阶段：财务危机潜伏期、财务危机发作期、财务危机的恶化期和财务危机实现期。
3）“三个月资金周转表”分析法
这种方法判断企业财务状况好坏的依据是“三个月资金周转表”的制定。其判断标准是：如果制定不出“三个月的资金周转表”，这本身就足个问题。这种方法的实质是企业面临着变幻无穷的的理财环境，所以要经常准备好安全度较高的资金周转表，假如连这种应当办到的事也做不到，就说明这个企业已经处丁紧张状态了。
4）管理评分法
这是由美国的仁翰·阿吉蒂提出的。这种评分法是基于这样一个前提：企业的失败源于企业的高级管理层。仁翰·阿吉蒂调查了企业的管理特性以及可能导致破产的公司缺陷，对这些缺陷、错误和征兆进行了对比打分，还根据这儿项对破产过程产生影响的大小程度对他们做了加权处理。
从以上对定性财务预警分析方法的论述中可以看出，定性方法虽然有简单、易懂、容易实施等优点，但其缺点亦非常明显，那就是定性分析法往往要受评价者个人主观意志的影响，而对于企业财务状况究竟如何，这种财务状况的发生究竟会对企业造成何种影响缺乏一个量化的解释。
②定量预警模式
通过对国内外文献的检索，有关财务预警的研究主要集中于定量方面，利用各种数学方法和工具，建立数学模型，对财务危机进行预测。文献报道的主要财务预警模型有45][4]：一是判定模型，二是回归分析模型，三是人工神经网络模型。
①判定模型
判定分析是对研究对象所属类别进行判别的一种多元统计分析方法。进行判别分析必须已知观测对象的分类和若干表明观测对象特征的变量值。判别分析就是要从中筛选出能提供较多信息的变量并建立判别函数，使推导出的判别函数对观测样本分类时的错判率最小。
1）一元判定模型
一元判定模型是以单个财务比率指标作为变量来判断企业是否处于破产状态，以单个财务比率指标的走势变化来预测企业财务危机的模型。在一元判定模型中，通常需要将样本分为两组：一组是构建预测模型的“预测样本”；另一组是测试预测模型的“测试样本”。当这些比率指标的值达到公司管理者设定的警戒值时，预警系统即应发出预警信号。
2）多元判定模型
多元判别模型是运用多种财务比率指标加权汇总而构造多元线性函数公式来对企业财务危机进行预测。其基本原理是：通过统计技术筛选出那些在两组间差别尽可能大而在两组内部的离散度最小的变量，从而将多个标志变量在最小信息损失下转换为分类变量，获得能有效提高预测精度的多元线性判别方程。多元判别模型的典型代表是Z值判别法和Fisher判别模型。
1）z值判别法
1968年，美国纽约大学商学院奥特曼（AlItman）教授在《金融杂志》上发表了《财务比率、判别分析和公司破产的预测》一文，奠定了多元判别模型的理论基础。奥特曼（Altman）教授多元线性判定模型又称z模型，即运用公司财务比率拟合多元线性函数方程，求出Z值，据以分析公司经营状况及发展趋势。奥特曼以1946年至1965年期间提出破产申请的33家企业和相对应的33家非破产企业为样本，运用数理统计分析的多元判别分析方法，结合会计数据拟合出了以下上市公司的Z分数模型：
Z=0.012X1+0.014X2+0.033X3+0.006X4+0.999X5 （式4.1）
X1=（期初流动资产一期末流动负债）/ 期末总资产
X2=期末留存收益 / 期末总资产
X3=息税前利润 / 期末总资产
X4=期末股东权益的市场价值 / 期末总负债
X5=本期销售收入 / 总资产
Z分数模型从企业的资产规模、折现力、获利能力、财务结构、偿债能力、资产利用效率等方面综合反映了企业财务状况，进一步推动了财务预警的发展。奥曼教授通过对Z分数模型的研究分析得出：Z值越小，该企业遭受财务失败的可能性就越大。美国企业的Z值的临界值为1.8。
2）Fisher判别模型
Fisher 判别法是一种线性判别的方法，该方法对两样本总体的要求很低，不需要两总体同为正态分布，不需要两者具有相同的协方差矩阵。Fisher判别法的指导思想为：对原始数据系统进行坐标变换，寻求能将总体尽可能分开的方向。
对于P维数据，Fisher判别法将寻求一个方向，将两组的P维数据在该方向上投影，使其投影的组与组之间尽可能地分开。如果要使得投影组点的组与组之间尽可能地分开，就相当于使组间的差异（即组间离差平方和SSG）尽可能的大，同时，又使每一组内差异（即组内离差平方和SSE）尽可能的小，这一优化准则可以表示为：
L（X1，X2，X3，……，Xp）=SSG/SSE→MAX
最后得到的判别函数的形式为：
Z=a1X1+a2X2+…+apXp （式4.2）
在总体只具有两类本时，利用回归分析所得到的回归方程和判别法则只差一个常数倍。因此，我们在进行财务危机判别时，只需假设危机组的因变量为0，非危机机组的因变量为1，就可以采用回归分析的方法直接计算Fisher判别法则的系数。
②回归分析法
回归分析法的基本思想是分析预测对象与有关因素的相互关系，用适当的回归预测模型（即回归方程）表达出来，然后再根据数学模型预测其未来状态。回归分析方法就是在大量实验观测数据的基础上，找出这些变量之间的内部规律性，从而定量的建立一个变量和另外多个变量之间的统计裹挟的数学表达式。常用的回归模型按变量之间的相互关系可分为多元逻辑（Logit）回归模型和多元概率比（Probit）回归模型。
1）多元逻辑（Logit）回归
多元线性回归可用于分析一个连续性因变量与一组自变量之间的关系，当因变量为分类变量时，需要研究分类变量与一组变量之间的关系，就要用多元逻辑回归。设P为某一事件发生的概率，1-P就为事件不发生的概率，将比数P/1-P取自然对数得In（P/1-P），即对P作Logit转换，记为logitP，则logitP的取值范围为一oo到+0之间。以logitP为因变量，建立线性回归方程：
logitP=a+β1x1+β2X2+ …+βnXn （式4.3）
可得：P=1/(1+exp(a+β_1 x_1+β_2 x_2+⋯+β_n x_n ) ) （式4.4）
2）多元概率比（Probit）回归模型
多元概率比回归的原理和Logit 回归类似，也是把求因变量和一组自变量之间关系的问题转化为求某一事件发生概率的问题，只是Logit 回归采用线性回归求解概率P，而Probit回归采用积分的方法求解，即

（式4.5）
参数a，b通过求似然函数的极大值得到。
③人工神经网络模型
人工神经网络（Artificial Neurd Network，ANN）作为一种平行分散处理模式，是对人类大脑神经运作的模拟。ANN除具有较好的模式识别能力（PatternRecognition）外，还可以克服统计方法的局限，因为它具有容错能力和处理资料遗漏或错误的能力。最为可贵的是，ANN还具有学习能力，可随时依据新的数据资料进行自我学习，并调整其内部的储存权重参数，以应对多变的企业环境。由于ANN具备上述良好的性质与能力，因而可以作为解决分类问题的一个重要工具。
4.1.2传统财务危机预警方法的局限性分析
上述介绍的三类财务危机预警建模采用的方法，在实际的应用过程中各有利弊，具体分析见表4.2。
表4.2 传统财务危机预警方法优缺点分析总结表

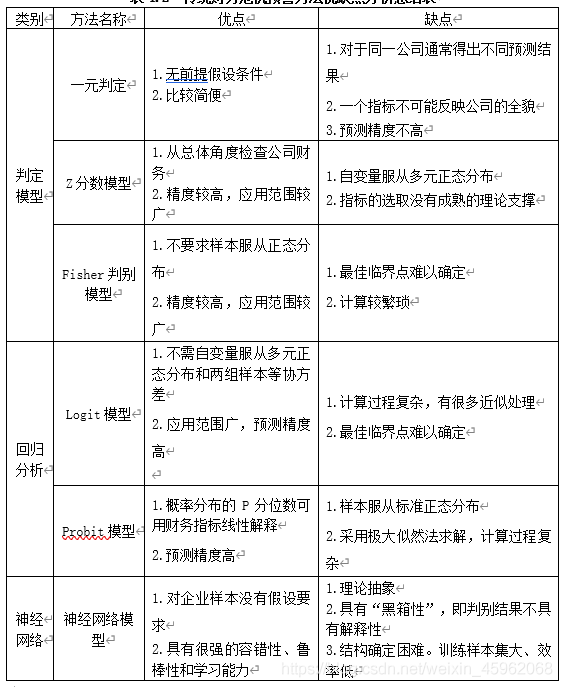
由表4.2分析可知，究竞哪一种方法是最恰当有效的预测方法，目前还难有定论。本文把两种方法结合起来，采用基于BP神经网络的组合预测方法建立财务危机预警模型。这种组合预测方法集合了统计模型和人工智能模型的优点，以期提高预测精度。
4.2 基于BP神经网络的非线性组合预测方法
4.2.1 组合预测方法
从信息论的角度来看，每一种预测方法都具有其独特的信息特征，是对事物内部结构的一种探索。因此，为了尽可能多地去利用全部有用信息，J.M.Bates和C.W.JGranger 1969年首次提出了“组合预测”的思想，并且得到了很大发展4951]。组合预测方法提倡对于同一个预测目标，最好不要只从一个角度着眼进行预测，而是从多个不同的方面系统地进行，这样就可以得到同一个预测目标的多个有一定差异的预测结果。组合预测理论认为这些结果各白所载有信息的价值是不同的，所以应该尽力将它们各自所载有的有价值的信息提取出来，用加权的方式把它们组合成一个综合的预测结果。
组合预测理论通过求个体预测值的加权算术平均而得到它们的组合预测值，在确定加权权重（也称组合权重）时，以组合预测误差方差最小为原则，这就是组合预测理论的组合原理5254。现以对两个个体预测进行加权组合为例阐述如下。

只要能近似得到ρ， 和 （ρ为两个体预测误差的相关系数），便可由（4.9）式得到权重k，最终由（4.7）式得到两个体预测值的组合预测值，也就是加权组合预测值。
Bates和Granger开创性地将两组时间序列预侧值进行加权平均组合，并对组合权重的确定进行了系统地研究，在此基础上，把组合预测的研究推广到三组或三组以上的时间序列值的组合，在国际预测界产生了一定的影响。

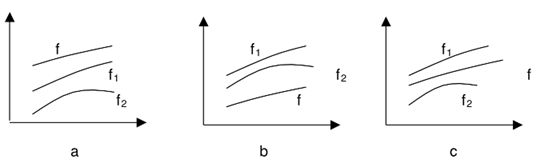
图4.1 线性组合方法的局限性
由于每一种预测方法都有其优点和局限性，很难断定哪一种预测方法针对某一问题优于其他方法。在先前不知道哪种方法优越时，线性组合方法能够以一种折衷的方式接近真实值，具有一定的应用价值。
但是线性组合方法有很多缺点，只有当这两种预测方法的其中一种估计值（f1）高于真实值（f），而另一种估计值（f2）低于真实值（f），此时把这两种预测方法进行线性组合，才能提高预测精度（如图4.1c所示）。而且加权平均组合隐含着这样一个强加的约束：预测对象的实际值总是介于f和f2之间，因而组合预测值可以取两个个体预测值的加权平均。事实上，预测对象的实际值x（t）与其预测值f，和f2之间的关系常常不满足那样的条件。由于客观上很多现象本身具有非线性，因此文新辉在1994年的一篇文章中首次提出了义组合预测原理非线性组合预测方法。
组合预测原理2：
设对于事件F有m种预测方法，那么可以用映射X∈X∈R"， 表示第i种预测方法。非线性组合预测原理是使用不同预测方法的非线性组合函数 进行预测，在某种测度之下， 的度量要比 （I=1.2…n）优越。
组合预测方法近年来引起我国学者的重视，唐小我、陈华友、蒋良奎等对组合预测的理论和方法作了深入的研究，其应用范围也逐渐扩大。
4.2.2 BP神经网络
人工神经网络（artificial neural network，简称ANN）是对生理上真实的人脑神经网络的结构和功能及基本特征进行理论抽象、简化和模拟而构成的一种信息系统，ANN作为一种并行分散处理模式，具有非线性映射、自适应学习和较强容错性的特点，可以对应多变的企业运作环境。BP人工神经网络是由D.E.Rumelhart和J儿McCelland及其领导的PDP（Paralld Distributed Processing）研究小组在1986年设计出来的。由于BP神经网络的神经元采用的传递函数通常是Sigmoid型可微函数，可以实现输入与输出间的任意非线性映射，因此在模式识别、风险评价、自适应控制等方而有着最为广泛的应用。
BP算法作为人工神经网络的一种比较典型的学习算法，它是由一个输入层、一个或多个隐层以及一个输出层组成，不仅含有输入输出节点，而且含有一层或多层隐节点，每一个节点的输出值由输入值、作用函数和阈值决定。当有信息输入时，输入信息送到输入节点，经过权值的处理传播到隐节点，在隐节点层经过各单元的特性为sigmoid型的激活函数（又称为作用函数、传递函数或映射函数等如F（x）=1/（1+e））运算后，送到输出节点，得到输出值让其与期望的输出进行比较，若有误差，则误差反向传播，逐层修改权系数，直到输出满足要求为止。最基本的三层BP人工网络结构如图4.2所示。

图4.2 BP神经网络结构简要示意图
人工神经网络（ANN）为广泛连接的巨型系统。人的大脑皮层是一个广泛连接的巨型复杂系统，ANN的连接机制模仿了人脑的这一特性。神经网络的特点有：
①神经网络具有很强的容错性，即人脑善于联想、类比和推广，对不完整的信息、扭曲的图像有很强的识别和纠正能力，能把不同领域内的知识结合起来，加以灵活运用。人工神经网络（ANN）有其并行结构和并行处理机制。人工神经网络（ANN）的分布式结构使其具有和人脑一样的容错性和联想能力。这类似人类和动物的联想记忆，当一个神经网络输入一个激励时，它要在已存储的知识中寻找与输入匹配最好的存储知识为其解。
②人工神经网络（ANN）具有自学习、自组织、自适应能力。大脑功能受先天因素的制约，但后天因素（如经历、学习和训练等）也起着重要作用。ANN很好地模拟了人脑的这一特性。如果最后的输出不正确，系统可以调整加到每个输入上去的权重以产生一个新的结果，最终达到所希望的输出。在训练过程中网络便得到了经验。由于这种自反馈，交替因果性不断地循环反复，使系统能够对其自身内部的关系以及它与外部的关系进行不断的自我调整，从而表现出自组织的特点。自适应功能是指不依靠外界强制性力量，而只依靠系统间充分的信息交换和反馈来实现整个系统间的平衡，要更好地适应变化着的外部环境。同时，神经网络有较强的鲁棒性，即是指控制系统在一定的参数摄动下，维持某些性能的特性。
神经网络学习的过程就是不断地总结经验的过程，类似人脑的活动。国际象棋大师在下每一步棋时，总要思考：这种棋局我以前见过吗，我原来时怎么下的，结果是对是错，到底哪种下法才是最优的。这就是所谓的“定式”。超级国际象棋大师一般能记忆5000种以上的棋局定式，并且能预测接下来的十部棋的大致走向。神经网络对财务数据进行分析的原理与之类似：对某一公司的一组财务数据，如果预测结果错误，那么就会反过来对模型的各个权值进行调整，这就象人脑一样，犯错后进行经验总结，避免以后再犯同样的错误。当神经网络学习到定程度，就能对些财务指标的组合产生一些“定式”，比如根据某一公司的一组财务数据，就能判断公司财务状况的好坏及其发展趋势。
传统的预测模型一般都把管理者的经验归结为定性的变量，而神经网络包含了“经验”这一定性因素，同时进行数据分析，达到了定性分析与定量分析的完美结合。
4.2.3 基于BP神经网络的组合预测方法
由于线性组合预测方法本身的局限性和企业财务危机系统的非线性特征，本文从非线性组合预测的角度采用基于BP神经网络的非线性组合预测方法来构建财务危机预警模型，采用Z值判别法和logistic 回归分析法两种预测方法得出的预测结果作为网络的输入，而实际的数据值作为网络的输出，各种预测方法在组合预测中的权重根据网络的自学习获得。
BP神经网络算法的步骤为[566]
①BP网络的初始化：确定各层节点的个数。将各个权值和阈值的初始值设为比较小的随机数，输入P个样本，m种预测方法的预测值作为输入向量Xki（k=1，2，3，… p；i=1，2，3，…，m）。各个实际数据为神经网络的输出Tk，对每个输入样本进行下面③到⑤的迭代。

⑥由误差函数E，判断E是否收敛到给定的学习精度以内（E≤拟定误差），如果满足，则学习结束否则转向步骤2继续进行。
⑦进行预测。
对某一学习样本使用上述算法，通过误差反向传播调整各层网络单元的权系数，输入所有学习样本，重复以上步骤，使输出误差限制在规定的范围内，此时权系数则不再改变。
4.3 基于BP神经网络的财务危机组合预警模型的构建
4.3.1 提出构建模型的基本假设前提
①所选取的样本企业在行业类型，企业的成长阶段等因素基本相同。在选取作为对照研究的样本的上市公司时，由于行业、企业规模等因素对企业的财务指标影响较大，为了控制这些干扰因素，我们采取了配对抽样的方法，选取116家制造行业的上市公司作为样本。
②所选取的企业所处的宏观环境（包括区域差异，经济政策等）具有大体一致性。将宏观经济周期、重大会计制度变化等因素可能造成的干扰尽量减少，从而使导致危机组与正常组之间财务特征差异化的变量集中于企业内部因素。
③每个公司的同一财务指标具有同方差，进入预测模型的指标之间无共线关系。
4.3.2 构建组合预警模型的步骤
在阐明了财务危机的概念、预警指标体系、模型的计量方法三个基本问题的基础上，构建基于BP神经网络的财务危机组合预警模型。构建组合预警模型的基本步骤如下：
第一步：设计研究样本
在明确财务危机概念的基础上，选择合适的财务危机公司和配对健康公司组成研究样本；第二步：搜集研究样本相关数据资料
在确定研究样本后，通过各种途径搜集研究样本所需的预警指标体系的若干年的相关数据资料；第三步：筛选预警指标体系
针对搜集的研究样本相关数据资料，运用显著性分析和因子分析法，对预警指标体系进行两次筛选，确定最终进入模型的指标变量；
第四步：构建单项预警模型
以上一步确定的预警指标变量为基础，选择应用较多的Z值判别分析法和Logistic回归方法，构建单项预警模型；
第五步：构建基于BP神经网络的财务危机组合预警模型以上述建立的Z值判别分析模型和Logistic回归模型作为单预测模型，运用BP神经网络建立组合预测模型。BP神经网络的设计包括输入层、隐含层、输出层、传递函数、训练函数等网络结构和网络参数的设置，具体到文本的研究，设置如下。
①输入层：本文以80家训练样本的z值判别分析模型和Logistic回归模型两个单预测模型的判别结果Z和Y组成的向量X=（ZY）作为组合预测模型的输入节点，即确定了2个输入节点。
②输出层：网络的输出层定义为一个节点，即上市公司的实际财务状况。在学习样本集中，i样本的输出量为y（当为ST公司时，y=1；当为非ST公司时，y=0）。
③隐含层：关于隐含层的层数有关文献证明在一定条件下，一个三层的BP神经网络可以任意精度去逼近任意映射关系，因此本文采用三层前向型神经网络结构。关于隐含层的神经元个数，一般只能根据经验，通过反复试验，本文采用隐含层神经元个数为36个。
④传递函数：传递函数的好坏对一个神经网络的学习效率至关重要。一般研究中都采用sigmoid型函数，考虑到输出层的期望输出数据为0或1，经反复测试，本文对输入层到隐含层的传递函数确定为log sigmoid型传递函数，隐含层到输出层之间的传递函数都确定为tan sigmoid型传递函数（即正切S型）。

⑤学习函数：本文选取了基于快速BP算法的学习函数learngdm，该算法在学习规则上选取了梯度下降动量学习函数。
⑥网络参数：目标误差0.05，学习速率为0.09，训练循环次数1000次。这样我们就用MATLAB语言，建立了一个2-36-1前向三层BP网络（程序见附表1）。
每一种预测方法都有其优点和局限性，本文以建立的Z值判别分析模型和Logistic回归预警模型对应的每个研究样本的判别值作为BP神经网络的输入向量，以研究样本所处实际状态为神经网络的输出，从而在各参加组合的模型预测结果与上市公司的实际状态之间建立一种非线性映射关系。经过不断地学习及测试，达到较高的精度之后，该模型就可以作为预测上市公司财务危机状态的非线性组合预测的有效工具。

第五章 上市公司财务预警模型的实证研究

5.1模型自变量的确定
根据指标确定的一定原则，本文在借鉴国内外学者的实证研究成果并结合我国上市公司的实际情况的基础上，从盈利能力、经营能力、偿债能力、成长能力和现金流量、表外信息六个方面构建上市公司财务危机预警的指标体系，包含25个预警指标（见表5.1），作为研究中使用的初始变量。然而模型中包括如此多的指标是不经济的，显得过于复杂，同时由于财务指标之间的相关性比较强，结构错综复杂，因此在建立模型前有必要对初始变量进行筛选。
表5.3 国内部分研究模型的财务比率列表

5.1.2 显著性分析
根据前人研究的思路，ST公司和非ST公司之间在财务指标上应该能够区别的，因此进入预警模型的指标至少能有效显著的区别ST公司和非ST公司，这是入选指标的必要条件。所以以此为标准本文采用统计分析法中的显著性检验方法（T检验）对预警指标进行第一次筛选。

零假设：ST公司的财务指标和非ST公司没有差异。
从以上的T检验结果可以看出：
在财务危机发生的前2年有14个指标通过了显著性检验，即净资产收益率、总资产报酬率、每股收益、成本费用利润率、总资产周转率、总资产增长率、现金流动负债比、每股营业现金流量、短期借款流动比率、审计意见类型、企业资产规模、存货周转率、资产负债率和流动比率14个指标通过显著性检验，其中总资产报酬率、每股收益、成本费用利润率、总资产周转率、总资产增长率、现金流动负债比、每般营业现金流量、审计意见类型8个指标在0.01水平上显著。而其他6个指标仅在0.05水平上显著。
根据T检验结果，我们选取总资产报酬率、每股收益、成本费用利润率、总资产周转率、现金流动负债比、每股营业现金流量、审计意见类型、净资产收益率、总资产增长率、每股营业现金流量、短期借款流动比率、企业资产规模、存货周转率、资产负债率和流动比率14个指标作为第一次筛选的入选变量。其中前8个指标在财务危机发生的前两年有很好的区分效果，所以引入预警模型。后6个指标虽然只是在0.05水平上显著性，但考虑到还要进行第二轮筛选，因此也把后6个作为入选变量，以期使得入选得指标更能反映公司的全貌。
5.1.3 因子分析
通过显著性检验，我们筛选出14个指标作为建立模型的第一次筛选的变量，然而这些指标有些相关性很强，包含了重复信息，为使模型更加精简，本文采用因子分析法对第一次筛的14个变量进行第二次筛选。
因子分析最早是由心理学家Karl PoarSon和CharleS Speamen在1904年提出的，它是从变量的相关矩阵出发将一个m维的随机向量X分解成低于m个且有代表性的公因子和一个特殊的m维向量，使其公因子数取得最佳的个数，从而使对m维随机向量的研究转化成对较少个数的公因子的研究。即用较少个数的公共因子的线性函数和特定因子之和来表达原来观测的每个变量，从研究相关矩阵内部的依赖关系出发，把一些具有错综复杂的变量归纳为少数几个综合因了子的一种多变量统计分析方法。该方法的本质就是通过降维技术将多个指标转化为少数几个综合指标，这些综合指标能够反映原始指标的绝大多数信息，并且所含有的信息互不重叠，彼此之间又不相关。
5.2基于BP神经网络的组合预测模型在公司财务预警中的应用
由于每一种预测方法都有其优点和局限性，很难断定哪一种预测方法针对某一问题优于其他方法。所以根据以上所选出的样本和预警指标变量，进行基于BP神经网络组合预警模型的构建。本文首先运用Z值判别分析方法和Logistic回归方法建立单项预测模型，然后以其预测结果作为基于BP神经网络的组合预测模型的输入变量，构建我国上市公司的财务危机预警模型，最后进行比较性分析。
为了使输入组合预测模型的Z值判别法和Logistic回归法的两种预测变量能从不同角度、不同层次反映企业的财务状况，本文在应用Z值判别模型时选用第一次筛选的14个财务指标作为模型的预警指标变量，在应用Logistic回归模型时选用第二次筛选的8个财务指标作为模型的预警指标变量。以期使得BP神经网络的组合预测模型取得较好的预测效果。
5.2.1 基于Z值判别分析的模型
本文以80家训练样本财务危机发生前两年的数据为基础，采用Z值线性判别分析法，建立判别分析模型，运用SPSS软件获得判别分析系数如下表。
表5.4 Z值判别分析变量系数表

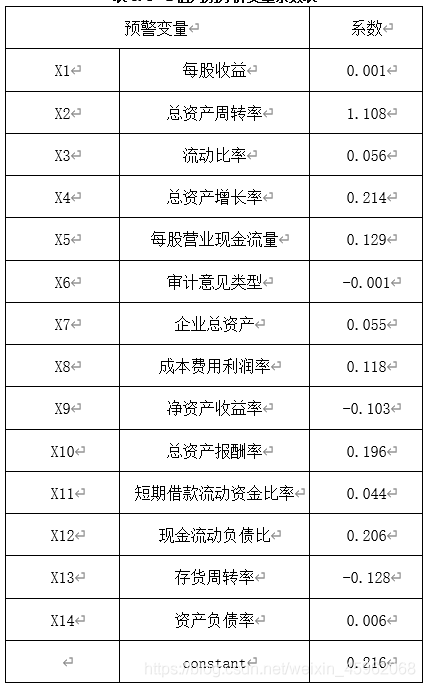
由此得到判别函数：
Z=0.216+0.001X1+1.108X2+0.056X3+0.214X4+0.129X5-0.001X6+0.055X7+0.118X8-0.103X9+0.196X10+0.044X11+0.206X12-0.128X13+0.006X14
根据判别模型，将训练样本财务危机发生前两年的数据进行回代，得到ST和非ST公司的平均Z值分别为一0.182和0.408。一般是取其平均数0.110为分界值，则两类样本的误判率一样。但是事实上，对于任何一个分割点，所有的模型都会犯两类错误：第一类错误（弃真错误）和第二类错误（取伪错误）。具体到本文研究中，弃真错误定义为将ST公司误判为非ST公司，而取伪错误指的是将非ST公司误判为ST公司。
实际中运用当中，为了满足谨慎性原则，把某一公司判为ST公司的概率应该明显要高于把它判为：ST公司，假设某一容量的样本公司的财务指标大致服从正态分布，处于中间区域的公司两年后可能变好也可能变坏，我们把财务状况处于中间偏上的10%也划归到ST公司行列。因此我们对ST和非ST公司的平均Z值一0.182和0.408，取二者之间的60%处的数0.171而不是50%的数0.110作为模型判别的临界值。若Z值小于0.171，则说明该公司未来两年内会被ST，否则即为财务健康公司。若Z值恰好等于0.171，则说明该公司的财务状况不够明朗，处于灰色地带，为谨慎起见，我们也将其归为ST行列。
对实证结果进行汇总，得到测试样本财务危机发生前2年的Z值判别分析模型预测结果汇总表，见表5.8。
表5.8 Z值判别分析模型一训练样本判别结果表

5.2.1 基于Logistic回归分析的判别模型
本文以80家训练样本财务危机发生前两年的数据为基础，使用上节筛选的8个指标为自变量，构建Logistic回归分析模型，假设ST公司的Y值为1，非ST公司的Y值为0，运用SPSS软件分析获得模型的系数及相关参数见表5.9。
表5.9 Logistic回归模型参数表一学习样本财务危机发生前两年

注：B为预警变量的回归系数；S.E.为回归系数的标准误差；Wald是检验偏回归系数的统计量；df为白由度；Sig.为显著水平。
根据表5.9，构建 Logistic回归模型为：

Logistic回归模型一般选择0.5作为分割点。Y但是事实上，对于任何一个分割点，所有的模型都会犯两类错误：第一类错误（弃真错误）和第二类错误（取伪错误）。具体到本文研究中，弃真错误定义为将ST公司误判为非ST公司，而取伪错误指的是将非ST公司误判为ST公司。理论上我们希望把模型的两类错误都降到最低水平，然而一类错误的减少意味着另一类错误的增加。
同样在实际中应用当中，为了满足谨慎性原则，把某一公司判为ST公司的概率应该明显要高于把它判为非ST公司，因此我们选择分割点应在尽量降低取伪错误的同时，优先满足降低弃真错误。而以0.5作为分割点则没有考虑到人们对于两类错误的承受能力的不同，因此本文选择以0.4作为分割点，以期能使预警模型在实际中有更好的预测效果。当Y值大于0.4时，判别为ST公司，数值越大，表明该公司未来一年内发生财务危机的可能性越大；当Y值小于0.4时，判别为非ST公司，数值越小，表明该公司财务状况越安全；当Y值等于0.4时，说明该公司的财务状况不太明朗，但是为谨慎起见，也判别为ST公司。
对以上实证结果进行汇总，得到测试样本财务危机发生前2年的Logistic回归模型预测结果汇总表，见表5.10。
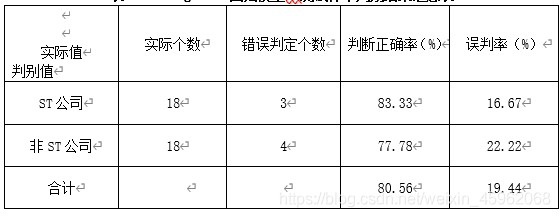
表5.10 Logistic回归模型一测试样本判别结果汇总表

5.2.3 基于BP神经网络的组合预测模型
以上述建立的Z值判别分析模型和Logistic回归模型作为单预测模型，运用BP神经网络建立组合预测模型。BP神经网络的设计包括输入层设2个输入节点、隐含层神经元个数为36个、输出层定义为一个节点、输入层到隐含层的传递函数确定为log sigmoid型传递函数，隐含层到输出层之间的传递函数都确定为tan sigmoid型传递函数、目标误差0.05，学习速率为0.09，训练循环次数1000次。用MATLAB语言，建立了一个2-36-1前向三层BP网络（程序见附表1）。
把36家测试样本的Z值判别模型和Logistic回归模型的判别结果输入到组合预测模型，得到输出结果如表5.11。
表5.11 基于BP神经网络的组合预警模型一测试样本判别结果表

由上表可知，ST公司有3家判错；非ST公司有3家判错，准确率为83.34%。模型对检验样本的判别率低于模型对训练样本的判别率。
5.2.4 模型测试结果比较
下面把三种模型针对36家测试样本的预测结果进行汇总，结果如下表5.12。
表5.12 预测结果比较一单预测模型与组合预测模型测试样本

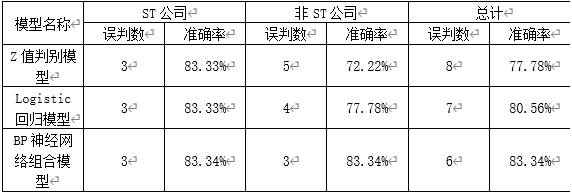
由表5.12，我们可以清楚地看到，在对36家上市公司的测试中。
①判别模型对于ST公司的判别准确率要高于非ST公司，这是由于在确定判别模型的临界点时，为满足谨慎性原则，尽量避免把ST公司误判为非ST公司，人为的加大了ST公司的判别区域（60%），提高对ST公司的判别准确率，得到了较好的预期效果。另外通过对单个误判样本的分析，笔者发现出现误判的样本都是处于ST和非ST临界状态的上市公司。
②Z值判别模型的判别准确率为77.78%，Logistic回归模型的判别准确率为80.56%。BP神经网络组合预测模型的总判别准确率为83.34%，明显高于前两种模型，可见组合预测模型集合了前两种模型的判别信息，并且神经网络模型较强的自我学习能力和容错能力，对样本所包含的数据信息的分析比较充分，有利于提高对主体不明的样本的判别能力，提高预测精度，具有较大的优越性。

第六章 结论

本文在总结国内外财务危机预警模型研究成果的基础上，以我国上市公司为研究对象，构建了基于BP神经网络方法的财务危机预警模型并进行了实证研究。其主要特色如下：
①由于不同行业和不同发展阶段企业的财务指标有一定的差距，在进行财务危机的预测时，把企业进行分类预测比不分类预测的预测结果好。所以本文选取制造行业的上市公司为研究对象，收到了较好的预测结果。该神经网络模型也可以以其他某行业的数据进行预测，进而推广到其他行业。
②经过主成分分析的预测模型更具有合理性，能把较多的原始预测变量筛选为较少的变量，而信息含量却没有什么减少，使得模型更易于计算和推广。本文把25个财务指标筛选为8个，大大地简化了计算工作量，使得模型更具有实用价值。③由于组合预测模型能够集合前两种模型的优点，为了使输入组合预测模型的z值判别法和Logistic 归法的两种预测变量能从不同角度、不同层次反映企业的财务状况，本文在应用Z值判别模型时选用第一次筛选的14个财务指标作为模型的预警指标变量，在应用Logistic回归模型时选用第二次筛选的8个财务指标作为模型的预警指标变量。以期使得BP神经网络的组合预测模型取得较好的预测效果。
④山于每一种预测方法都有其优点和局限性，很难断定哪一种预测方法针对某问题优于其他方法。本文集合统计模型和人工智能模型的优点，以Z值判别模型和Logistic回归模型的预测结果作为输入变量，构建了基于BP神经网络的财务危机组合预测模型，该模型克服了统计方法对样本的严格限制和神经网络方法的黑箱性等缺陷，充分利用了人神经网络模型容错性、学习性和统计方法的优点研究结果表明，在上市公司财务危机发生前两年有83.34%的判断准确率，优于Z值判别模型和Logistic回归模型，具有很好较高的预测精度和适用性。

参考文献

[1]余廉等.企业预警管理实务[M]，河北科学技术出版社，1999,42
[2]周首华陆正飞汤谷良：现代财务理论前言专题[M]，东北财经大学出版社2000
[3]邵屹.中国上市公司财务失败预警模型的实证研究：[学位论文].北京：首都经济贸易大学，2004,3
[4]李晶.引入信息修正因素的上市公司财务危机预警系统的构建：[学位论文].沈阳：沈阳工业大学，2004,3
[5]殷尹，梁梁，吴成庆，财务困境概率贝叶斯估计[J]，系统工程理论方法与应用,2004,2
[6]飞思科技产品研发中心.MATLAB6.5辅助神经网络分析与设计[M].北京：电子工业出版社,2003
[7]李秉祥.我国上市公司被特别处理的组合预测模型研究[J]，运筹与管理，2004,6
[8]鲍一丹，吴燕萍，何勇，BP神经网络最优组合预测方法及其应用[J]，农机化研究,2004,5
[9]胡平，康玲.一种基于非线性组合预测方法在径流测报中的应用[J]，人坝与安全,2001,6
[10]蒋良.一种在组合预测中确定变权系数的方法（J），上海海运学院学报，20023
[12]文新辉，牛明洁.一种新的基于神经网络的非线性组合预测方法[J].系统工程理论与实践，1994,12
[13]苏金明，傅荣华等.统计软件SPSS系列应川实战篇[M]，北京，电了子工业出版社，2004
[14]周昌仕，李森木.企业财务预警分析模型及其运用[J]，湛江海洋大学学报，2003,4、

附录1 BP算法

x为输入向量
Y为目标向量
m为测试向量
MATLAB代码如下
%录入输入向量P和目标向量T
P=[x]2×80矩阵，T=[Y]1×80矩阵
%输入向量的最大值和最小值，2×80矩阵
threshold-2×80矩阵
net=netff
net=netff（minmax（P）,[36,1],{‘logsig’,‘tansig’},‘trainlm’，‘learngdm’）;
%训练次数为1000，训练日标为0.05，学习速率为0.09
net.trainParam.show=100;
net.trainParam.epochs=1000;
net.trainParam.goal=0.05;
LP.Ir=0.09;
net=train（net,P,T）;
z=sim（net，P）;
%测试网络：
%输入测试数据Pt
Pt=[m]2×36矩阵
z=sim（net，Pt）

附录2

1、数据读取和处理

1.	import numpy as np  
2.	import pandas as pd  
3.	path = r'D:Documentspython_documentsPractical Business Data AnalysiscaseCH4st.csv'
4.	data = pd.read_csv(path)  
5.	data.head()

2、参数估计
用似然比对整体的显著性进行检验。
（1）先以空模型进行逻辑回归：

1.	import pandas as pd
2.	import statsmodels.formula.api as smf 
3.	import statsmodels.api as sm
4.	import pylab as pl
5.	import numpy as np
6.	 
7.	 
8.	glm0_1999 = smf.glm('ST~1', data_1999, family=sm.families.Binomial(sm.families.links.logit))
9.	res = glm0_1999.fit()
10.	print(res.summary())

（2）再以全模型进行逻辑回归：

1.	import statsmodels.formula.api as smf 
2.	import statsmodels.api as sm
3.	 
4.	glm1_1999_logit = smf.glm('ST~ARA + ASSET + ATO + GROWTH + LEV + ROA + SHARE', data_1999,
5.	                          family=sm.families.Binomial(sm.families.links.logit))
6.	res_logit = glm1_1999_logit.fit()
7.	print(res_logit.summary())

（3）全模型的probit回归：

1.	import statsmodels.formula.api as smf 
2.	import statsmodels.api as sm
3.	 
4.	glm1_1999_probit = smf.glm('ST~ARA + ASSET + ATO + GROWTH + LEV + ROA + SHARE', data_1999,
5.	                           family=sm.families.Binomial(sm.families.links.probit))
6.	res_probit = glm1_1999_probit.fit()
7.	print(res_probit.summary())

3、模型选择
（1）logit回归基于AIC的变量选择：

1.	X = data_1999.drop('ST',axis=1)
2.	Y = data_1999['ST']
3.	import statsmodels.api as sm
4.	import itertools
5.	 
6.	predictorcols = list(X.columns)   #将各个自变量汇成一个列表
7.	AICs = {}
8.	for k in range(1, len(predictorcols)+1):
9.	    #print(k)
10.	    for variables in itertools.combinations(predictorcols, k):
11.	      
12.	        predictors = X[list(variables)]
13.	        predictors2 = sm.add_constant(predictors)
14.	        est = sm.Logit(Y, predictors2)
15.	        res = est.fit()
16.	        AICs[variables] = res.aic
17.	 
18.	from collections import Counter
19.	c = Counter(AICs)   
20.	c.most_common()[:-4:-1] 

（2）查看三个变量的logit拟合结果：

1.	import statsmodels.formula.api as smf 
2.	import statsmodels.api as sm
3.	 
4.	glm1_1999 = smf.glm('ST~ARA + GROWTH + LEV', data_1999, family=sm.families.Binomial(sm.families.links.probit))
5.	res_aic_probit = glm1_1999.fit()
6.	print(res_aic_probit.summary())

（3）用BIC准则进行logit的变量选择：

1.	import statsmodels.api as sm
2.	import itertools
3.	 
4.	predictorcols = list(X.columns)   #将各个自变量汇成一个列表
5.	BICs = {}
6.	for k in range(1, len(predictorcols)+1):
7.	    #print(k)
8.	    for variables in itertools.combinations(predictorcols, k):
9.	        #Python itertools模块combinations(iterable, r)方法可以创建一个迭代器，
10.	        #返回iterable中所有长度为r的子序列，返回的子序列中的项按输入iterable中的顺序排序。
11.	        predictors = X[list(variables)]
12.	        predictors2 = sm.add_constant(predictors)
13.	        est = sm.Logit(Y, predictors2)
14.	        res = est.fit()
15.	        BICs[variables] = res.bic
16.	 
17.	from collections import Counter
18.	c = Counter(BICs) 
19.	c.most_common()[:-4:-1] 

（4）probit回归的AIC选择：

1.	import statsmodels.api as sm
2.	import itertools
3.	 
4.	predictorcols = list(X.columns)   #将各个自变量汇成一个列表
5.	AICs = {}
6.	for k in range(1, len(predictorcols)+1):
7.	    #print(k)
8.	    for variables in itertools.combinations(predictorcols, k):
9.	        #Python itertools模块combinations(iterable, r)方法可以创建一个迭代器，
10.	        #返回iterable中所有长度为r的子序列，返回的子序列中的项按输入iterable中的顺序排序。
11.	        predictors = X[list(variables)]
12.	        predictors2 = sm.add_constant(predictors)
13.	        est = sm.Probit(Y, predictors2)
14.	        res = est.fit()
15.	        AICs[variables] = res.aic
16.	 
17.	from collections import Counter
18.	c = Counter(AICs) 
19.	c.most_common()[:-4:-1]

（5）probit回归的BIC选择：

1.	import statsmodels.api as sm
2.	import itertools
3.	 
4.	predictorcols = list(X.columns)   #将各个自变量汇成一个列表
5.	BICs = {}
6.	for k in range(1, len(predictorcols)+1):
7.	    #print(k)
8.	    for variables in itertools.combinations(predictorcols, k):
9.	        #Python itertools模块combinations(iterable, r)方法可以创建一个迭代器，
10.	        #返回iterable中所有长度为r的子序列，返回的子序列中的项按输入iterable中的顺序排序。
11.	        predictors = X[list(variables)]
12.	        predictors2 = sm.add_constant(predictors)
13.	        est = sm.Probit(Y, predictors2)
14.	        res = est.fit()
15.	        BICs[variables] = res.bic
16.	 
17.	from collections import Counter
18.	c = Counter(BICs) 
19.	c.most_common()[:-4:-1]

欢迎大家加我微信学习讨论