OpenFOAM 网格拓扑与计算表面向量和 (1)
OpenFOAM 网格拓扑与计算表面向量和 (1)
OpenFOAM采用非结构化网格,从而在网格类型和网格加密方面更加具有灵活性。
在OpenFOAM中,网格单元 (cell)、网格面 (face)、点 (point)都被按照特定结构进行拓扑排序。
OpenFOAM 运行blockMesh指令生成网格文件 constant/polyMesh,其中主要包含 boundary、 faces、 neighbour、 owner、 points五个文件 (在不考虑添加faceZone或者cellZone的情况下)。
从blockMesh的日志文件中也可以看出相关信息 (网格总量 4×4×1):
Writing polyMesh
----------------
Mesh Information
----------------
boundingBox: (0 0 0) (1 1 0.1)
nPoints: 50
nCells: 16
nFaces: 72
nInternalFaces: 24
----------------
Patches
----------------
patch 0 (start: 24 size: 4) name: movingWall
patch 1 (start: 28 size: 12) name: fixedWalls
patch 2 (start: 40 size: 32) name: frontAndBack
End
其中 nPoints表示构成所有cells的点的数量,ncells表示网格的数量,nFaces为面的数量,nInternalFaces为内部面的数量。
(1) 点 (points)
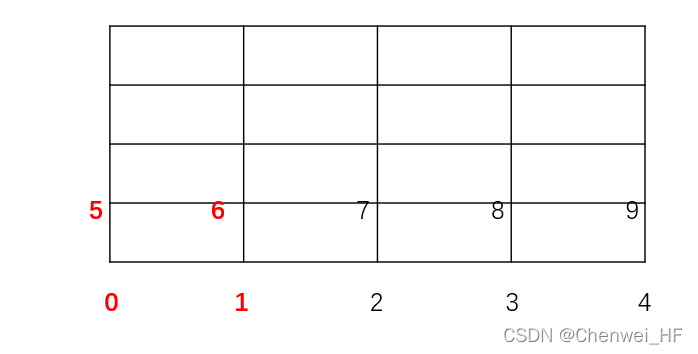
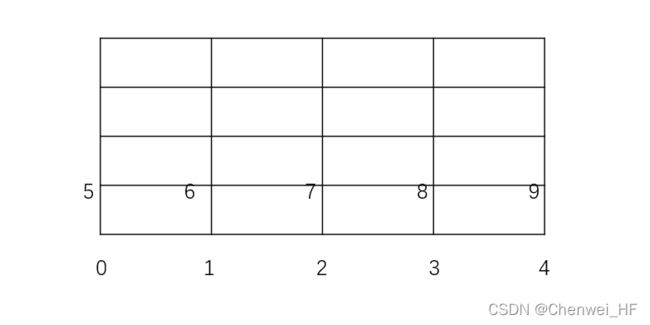
接下来,我们在constant/polyMesh/points文件中可以看到 points的总数为50 (仅列举部分),可以很明显的看出来points是按照 x→y→z 的顺序排列,作二维简化之后如图所示。
FoamFile
{
version 2.0;
format ascii;
class vectorField;
location "constant/polyMesh";
object points;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
50
(
(0 0 0) // points 0
(0.25 0 0)
(0.5 0 0)
(0.75 0 0)
(1 0 0)
(0 0.25 0)
(0.25 0.25 0)
(0.5 0.25 0)
(0.75 0.25 0)
(1 0.25 0) // points 9
...
我们打开constant/polyMesh/faces文件,可以看到faces的总数为72 (仅列举部分)。每个面包含4个point,例如:组成第一个面的四个顶点序号为分别为1, 6, 31, 26,顶点排列遵循面法向量指向block内部的准则。
FoamFile
{
version 2.0;
format ascii;
class faceList;
location "constant/polyMesh";
object faces;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
72
(
4(1 6 31 26)
4(5 30 31 6)
4(2 7 32 27)
4(6 31 32 7)
4(3 8 33 28)
4(7 32 33 8)
...
(2) 面 (faces)
OpenFOAM的面拓扑按照内部面→边界面的顺序。我们可以在constant/polyMesh/boundary中看出各个边界 (boundary patch) 的边界面 (boundary faces) 起始序号和数量,在本算例中,共有三个patch:movingWall、fixedWalls、frontAndBack。
其中,我们可以看到边界movingWall的 s t a r t F a c e = 24 startFace=24 startFace=24,等于 I n t e r n a l F a c e InternalFace InternalFace的总量;
而 f r o n t A n d B a c k 的 s t a r t F a c e = 40 , n F a c e s = 32 frontAndBack的startFace = 40, nFaces = 32 frontAndBack的startFace=40,nFaces=32,说明边界 f r o n t A n d B a c k frontAndBack frontAndBack从第40个面开始,总共包含32个面 ( 16 × 2 ) (16 × 2) (16×2)
FoamFile
{
version 2.0;
format ascii;
class polyBoundaryMesh;
location "constant/polyMesh";
object boundary;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
3
(
movingWall
{
type wall;
inGroups 1(wall);
nFaces 4;
startFace 24;
}
fixedWalls
{
type wall;
inGroups 1(wall);
nFaces 12;
startFace 28;
}
frontAndBack
{
type patch;
nFaces 32;
startFace 40;
}
)
那么,我们再次打开constant/polyMesh/faces文件,找到第40个face:
...
4(3 4 29 28)
4(0 5 6 1) // frontAndBack的startFace
4(5 10 11 6)
...
(3) 内部面 (InternalFaces)
有了以上的基本理解之后,我们可以进一步探究OpenFOAM的面拓扑。在OpenFOAM的计算中,涉及到梯度的计算,定义变量 Φ Φ Φ在有限体积单元形心处的平均梯度[1]:
∇ Φ c ‾ = 1 V c ∫ V c ∇ Φ d V \overline{\nabla \Phi_{c}} = \frac{1}{V_c}\int_{Vc} \nabla \Phi dV ∇Φc=Vc1∫Vc∇ΦdV
应用散度定理,将体积分转换为表面积分,并且针对于离散单元面的情况有:
∇ Φ c ‾ V c = ∑ f ∼ n b ( c ) Φ f ‾ S f \overline{\nabla \Phi c} Vc = \sum\limits_{f \sim nb(c)} \overline{\Phi_f} S_f ∇ΦcVc=f∼nb(c)∑ΦfSf
其中, f ∼ n b ( c ) f \sim nb(c) f∼nb(c)代表cell C的各个面。
在OpenFOAM,因为一个面只存储一个对应的法向量,所以规定:面法向量从 c e l l ( k ) cell (k) cell(k) 指向序号大于 k k k 的 c e l l cell cell 时为正,反之则为负,如下图所示[1],于是 c e l l ( k ) cell (k) cell(k) 梯度的计算式可以写成:
∇ Φ k ‾ = − 1 V k ( − ∑ n = ( f ∼ n b ( k ) ) < k Φ n ‾ S n + ∑ n = ( f ∼ n b ( k ) ) > k Φ n ‾ S n ) \overline{\nabla \Phi_k} = -\frac{1}{V_k}(-\sum\limits_{n = (f \sim nb(k)) < k} \overline{\Phi_n} S_n + \sum\limits_{n = (f \sim nb(k)) > k} \overline{\Phi_n} S_n) ∇Φk=−Vk1(−n=(f∼nb(k))<k∑ΦnSn+n=(f∼nb(k))>k∑ΦnSn)
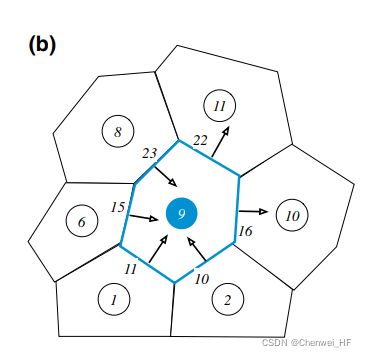
这样的拓扑结构就需要界定两个 c e l l cell cell 之间的内部面 ( I n t e r n a l F a c e ) (InternalFace) (InternalFace) 中 f a c e face face 与 c e l l cell cell 的 从属关系,于是OpenFOAM在生成 f a c e face face 时,同样生成了 f a c e face face 的本网格— o w n e r owner owner与 相邻网格— n e i g h b o u r neighbour neighbour,如下:
constant/polyMesh/owner:
FoamFile
{
version 2.0;
format ascii;
class labelList;
note "nPoints: 50 nCells: 16 nFaces: 72 nInternalFaces: 24";
location "constant/polyMesh";
object owner;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
72
(
0
0
1
1
2
2
3
...
constant/polyMesh/neighbour:
FoamFile
{
version 2.0;
format ascii;
class labelList;
note "nPoints: 50 nCells: 16 nFaces: 72 nInternalFaces: 24";
location "constant/polyMesh";
object neighbour;
}
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
24
(
1
4
2
5
3
6
7
5
...
其中, o w n e r = 72 = n F a c e s owner = 72 = nFaces owner=72=nFaces,代表每个 f a c e face face都有一个对应的本网格,而 n e i g h b o u r = 24 = n I n t e r n a l F a c e s neighbour = 24 = nInternalFaces neighbour=24=nInternalFaces代表每个内部面都会有一个相邻网格。
至此,完成了对OpenFOAM的网格拓扑介绍,如果有理解不正确的地方欢迎大家指正。下一节会以实操的形式介绍对OpenFOAM面法向量的计算。
参考文献如下:
[1] Moukalled F, Mangani L, Darwish M. The finite volume method[M]//The finite volume method in computational fluid dynamics. Springer, Cham, 2016: 103-135.