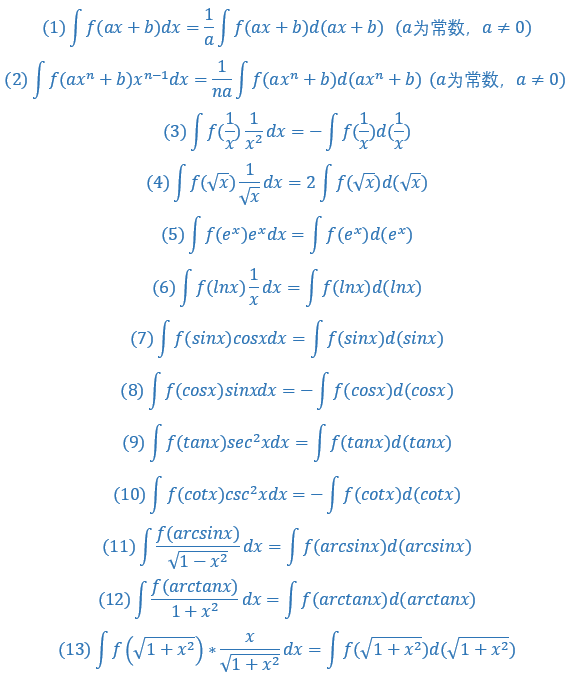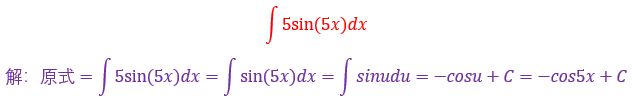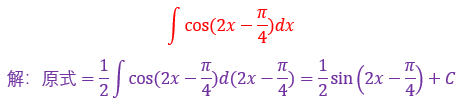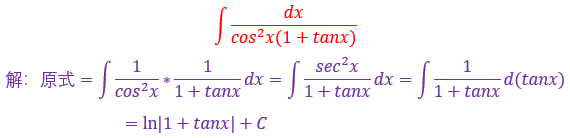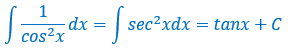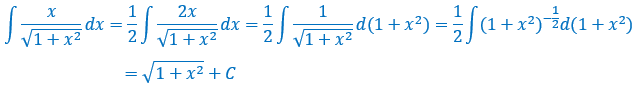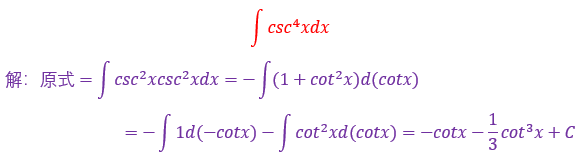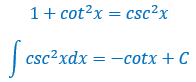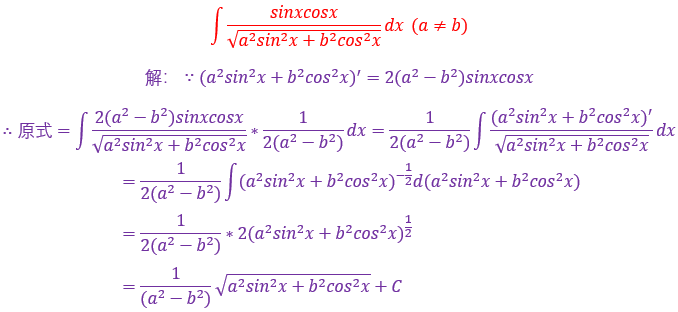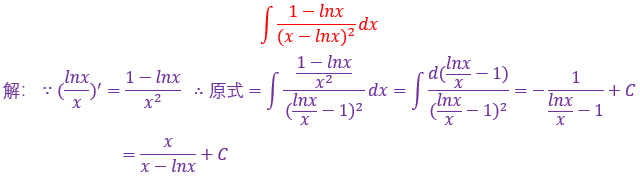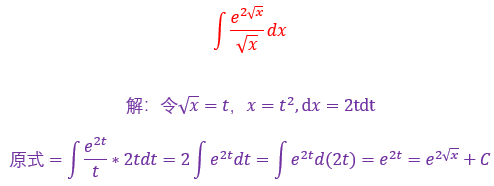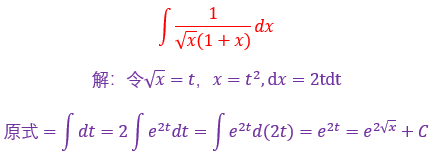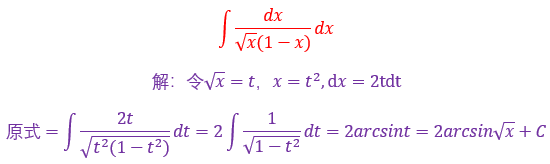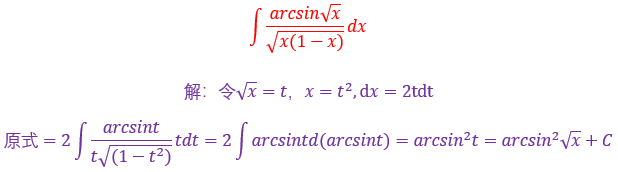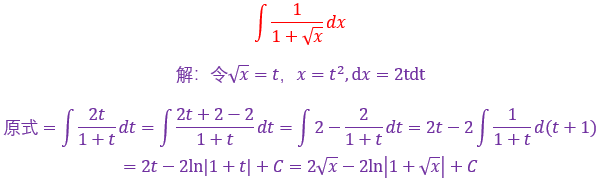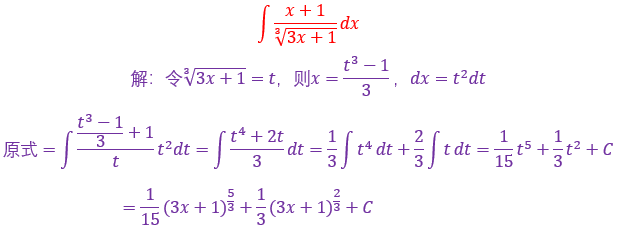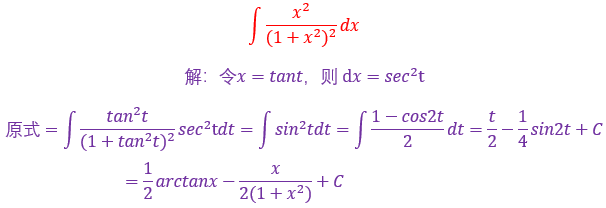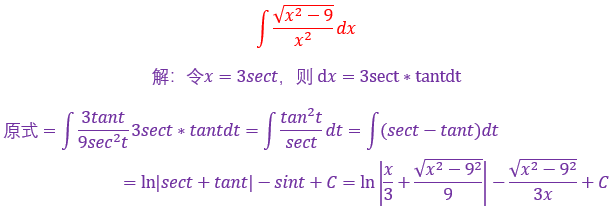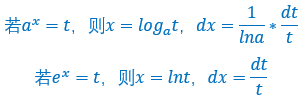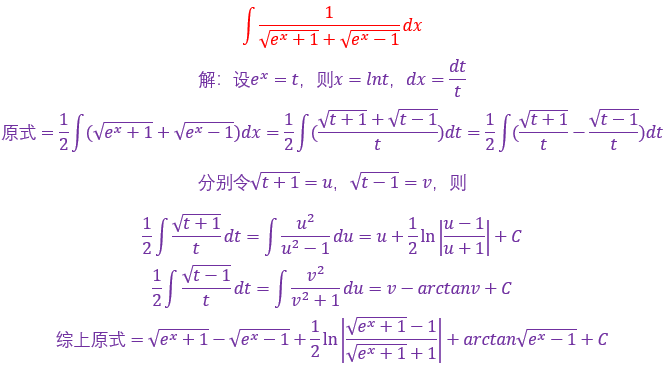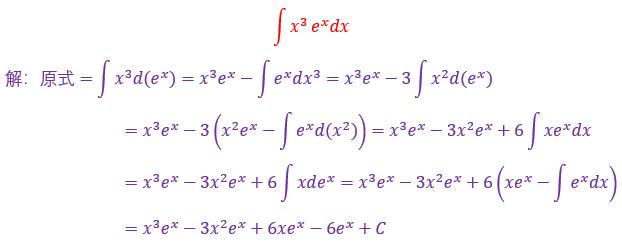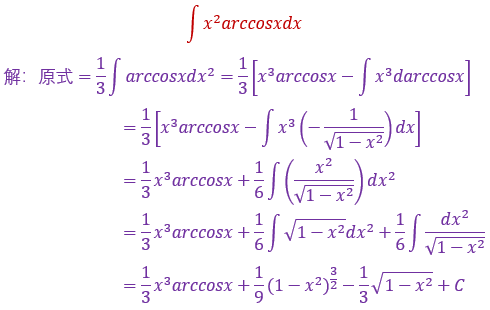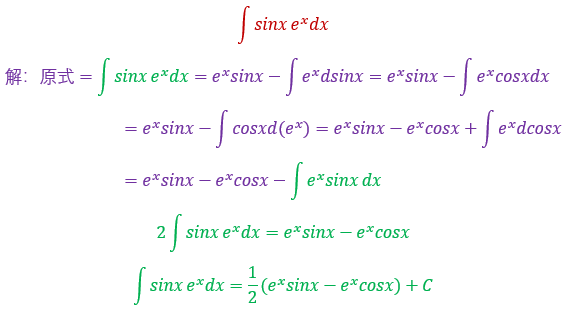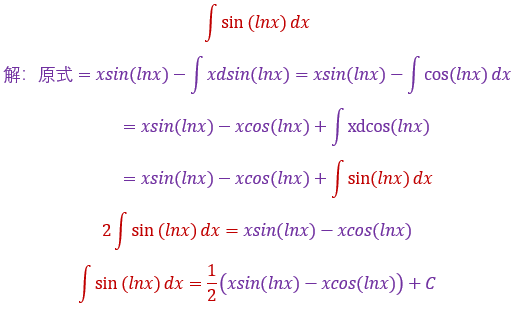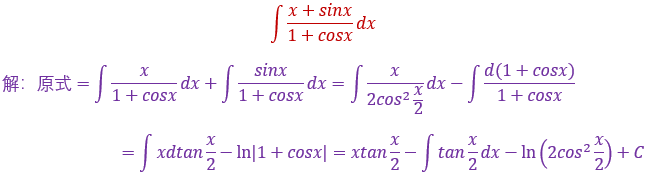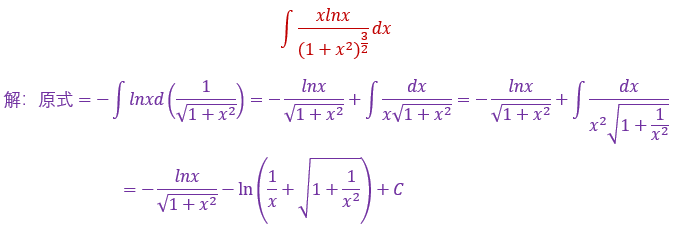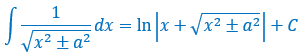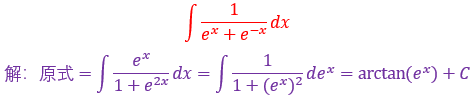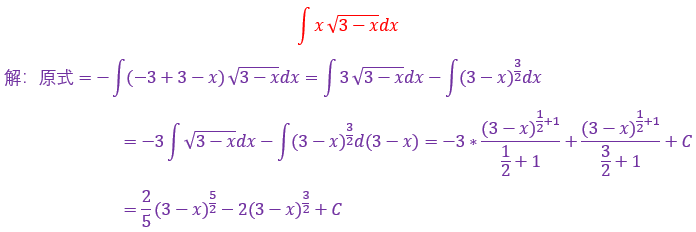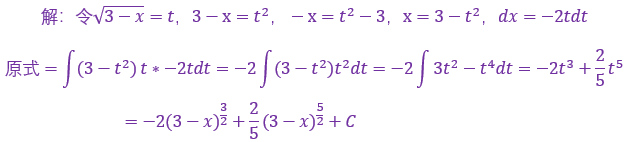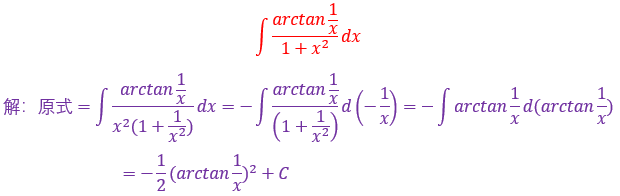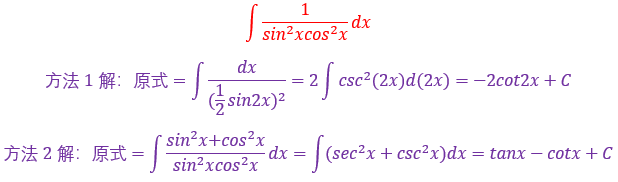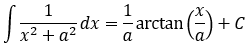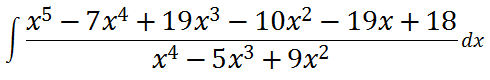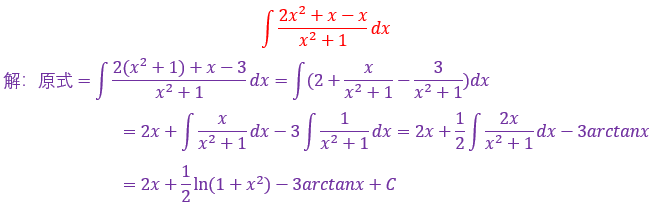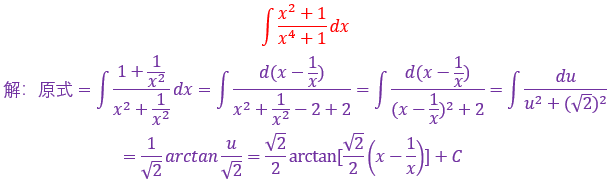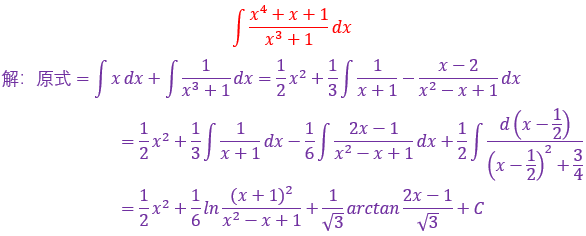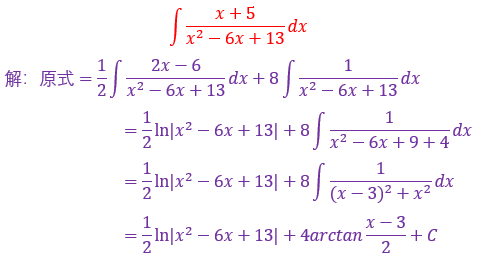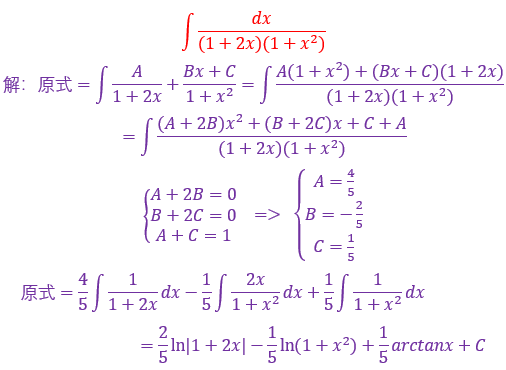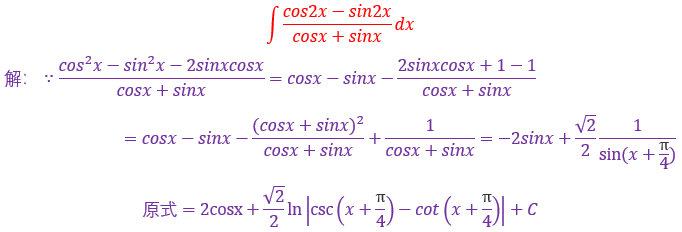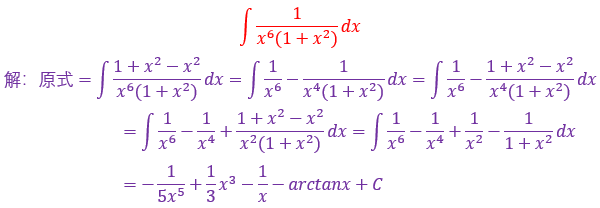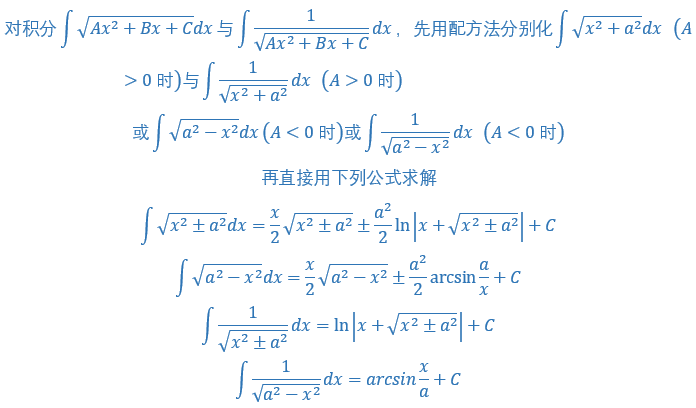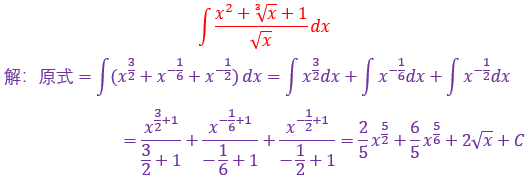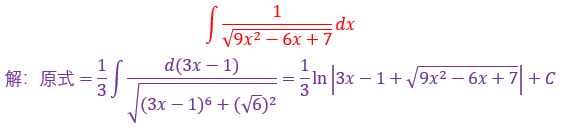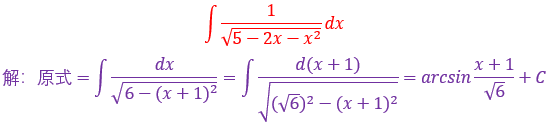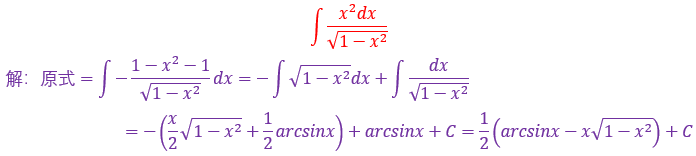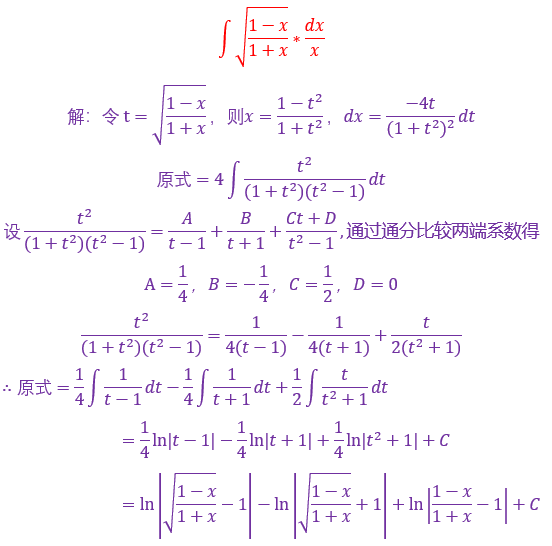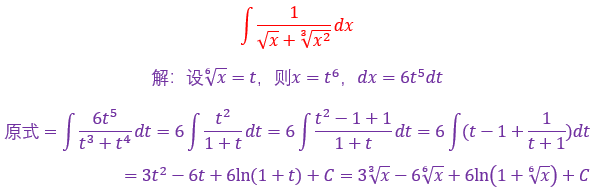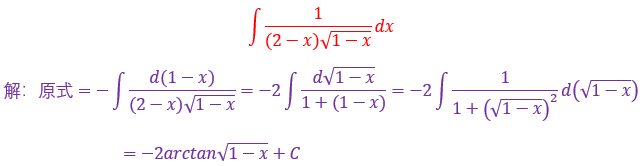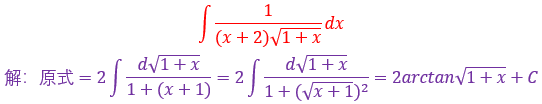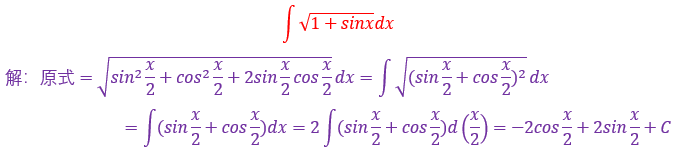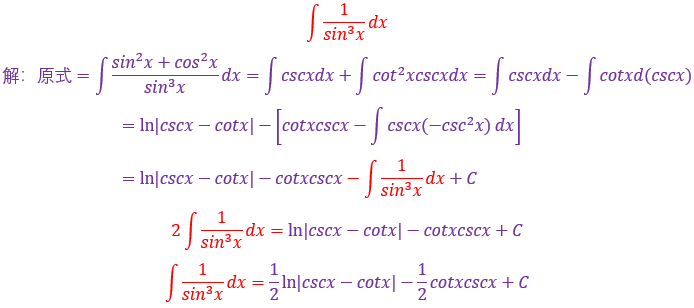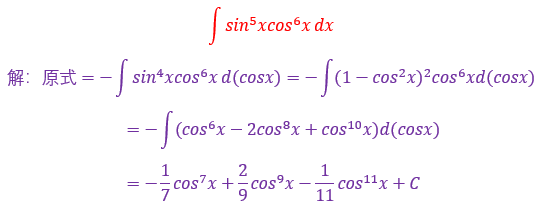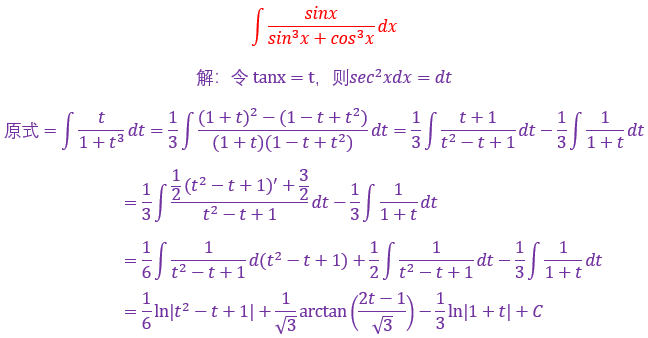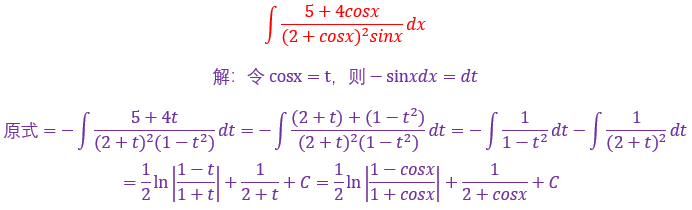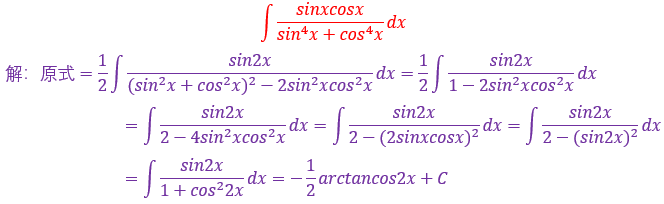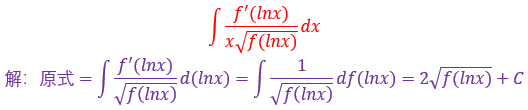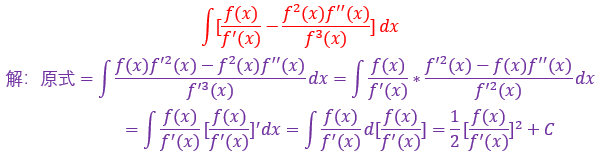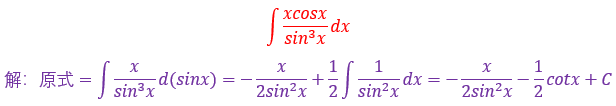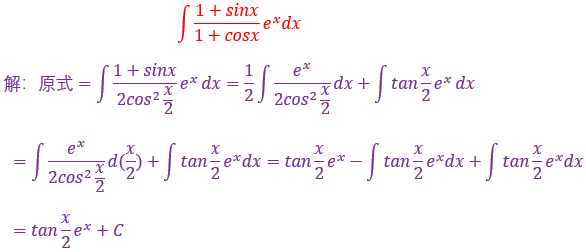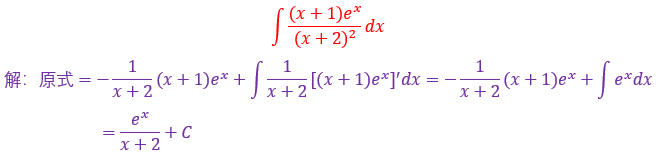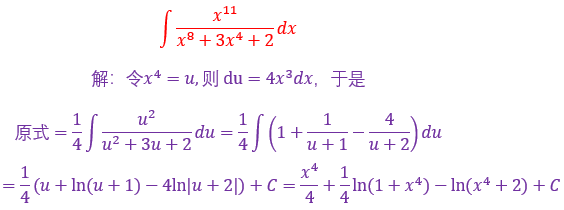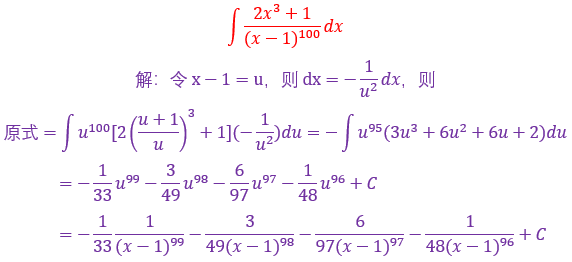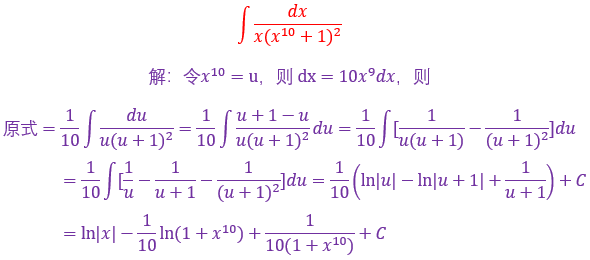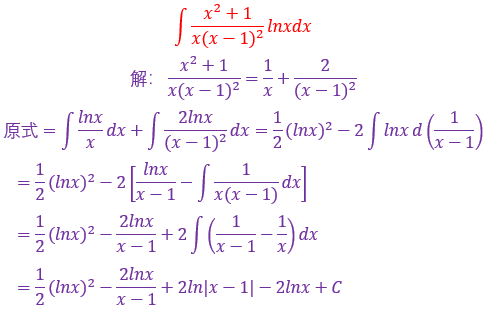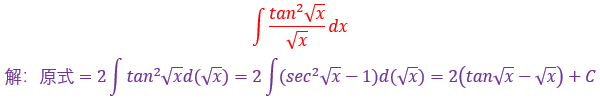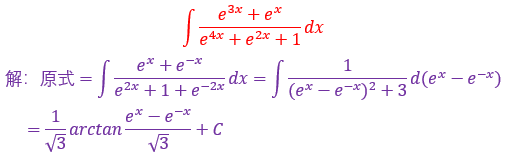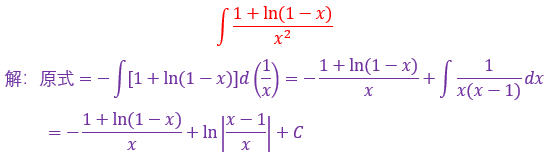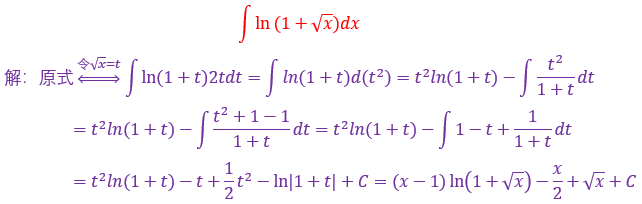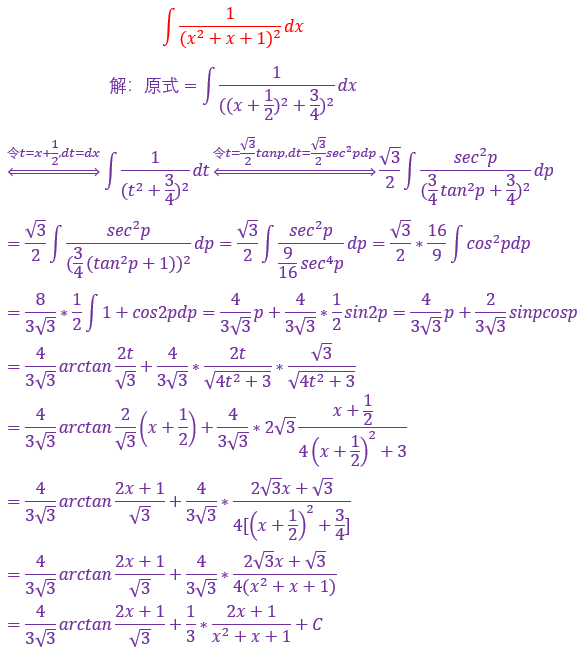不定积分24个基本公式_不定积分计算—典型题及解题技巧
前言:想起专接本的时候,不定积分的计算可把我折磨惨了,现在好点了,遇到大部分的题目知道该怎么解了,但是有些题还是属实让我有些苦恼,我在这里写一篇超长文章来进行对症下药,也希望给大家一些帮助,参考书目我会放在最后
这或许是有史以来本公众号以来最长文章
这也或许是我近一年最后一次写大篇幅文章
今年就要考研了,请允许我自私一次,以后少更文了,感谢以来大家对我的支持,笔芯
正文:
题型Ⅰ—利用凑微分法求不定积分
解题思路:把被积函数和相似基本积分公式进行比较,被积函数中找到复合函数,大概率复合函数是突破口,用复合函数以外的元素进行凑复合部分,再用基本积分公式从而达到化简的效果
一些常见的凑微分的形式我放在这里
1.
经分析可以看出sin5x是复合函数,而复合部分就是5x
恰好5x的导数就是5,也就是说∫5dx=5x+C,所以把5放到微分后面
设5x=u,再利用∫sinx=-cosx+C基本积分公式进行求解
熟练了以后中间设u这一步可以不用写
2.
复合函数为cos(2x-π/4),复合部分为2x-π/4
而放眼望去什么也没有啊,此时要返回来想(2x-π/4)的导数是谁?
是2啊,π/4是常数,常数的导数为0,∫2dx=2x+C
多出来的2倍需要在前面乘以1/2平衡系数即可完成
3.
千万不要被他的外表所吓倒,以为100次方就很难解
还是冷静地分析,复合函数为(1+x²)^100,复合部分为1+x²
剩余部分还有个x,想起2x的原函数不就是1+x²吗?
前面乘以1/2平衡系数即可完成
4.
这个题咋一看也是,(e^(e^x)+x)什么玩意
但是如果你能联想到指数函数的性质
![]()
那应该就没什么问题了
5.
这个题很有特点的是分母是由两部分相乘而成,而分子上什么也没有
恰好本题解决关键不是去凑cos²x,而是去凑1+tanx,要知道
6.
本题难点在于如果你不知道复合的部分和剩余部分是什么关系
就很难处理往往被搞得很复杂,所用的guo'ch
7.
本题属于一类题型,需要各位注意一下,之前的文章里有提到过,链接如下
不定积分—sinx与cosx型(可点击)
在这里放一下我总结的结论,应该是没问题的
8.
这个题明显比前面几个稍微上了点难度,做本体的关键在于你要知道两个公式
9.
这个其实算跟BT类型了,我曾经还做到一个凑微分的,我硬是找不到怎么凑
本质还是找复合函数复合部分跟其他部分比较找关联
10.
这个就是我所说的很BT的题,我不看答案实在想不起来到底该怎么凑
甚是苦恼,估计过个几天再回头做没多少印象了
题型Ⅱ—利用变量代换法求不定积分
解题思路:将被积函数与相似的基本积分公式作比较是做这一题型的基本思路
如何进行变量替换,以下是常见的变量替换表格
11.
12.
13.
14.
15.
16.
本题就非常典型,属于标准的变量替换法,其实凑微分跟它有点交集,本质都是换元,遇到根号要条件反射,想起整体替换,分子要想和分母相消一定要想到+n-n这个技巧,然后再用基本积分公式计算,属于入门难度
17.
要学以致用鸭,上面说到了,遇到根号要想到什么?对,想起根号整体替换,因为要消掉根号鸭,然后把常数提到不定积分号的外面再用基本积分公式进行求解计算即可
18.
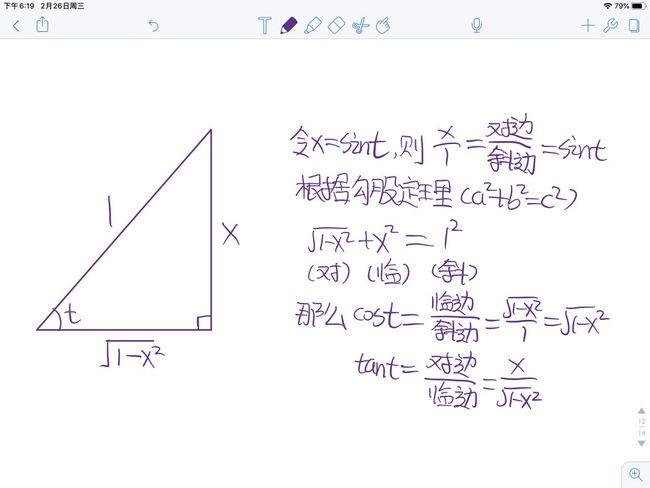
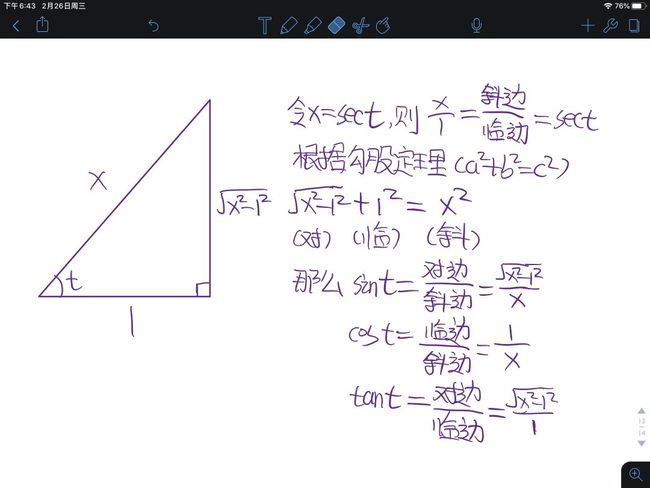
遇到a²-x²,要想到三角代换,令x=asint,则dx=acostdt,三角代换方法我放在这里
另外解决这个题还需要一个公式,还需要注意一些点
ln(a*b)=lna+lnb,ln(a/b)=lna-lnb
19.
遇到a²+x²,要想到三角代换,令x=atant,则dx=asec²tdt
具体不会的操作可以看上面的我用ipad截图的图片,相信会对你有帮助
20.
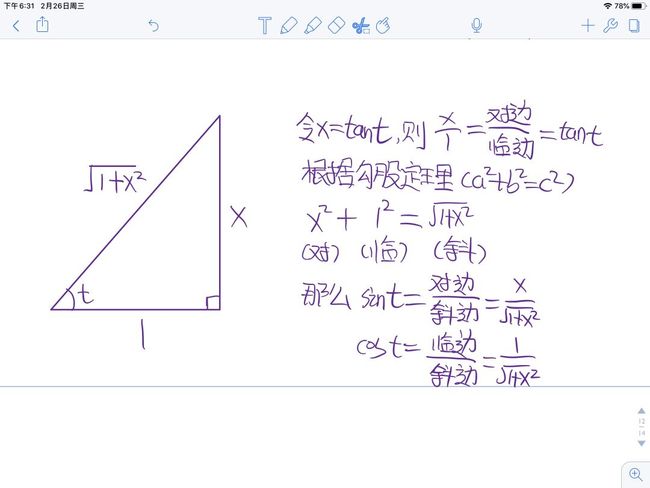
遇到x²-a²,要想到三角代换,令x=asect,则dx=asecttantdt
这里需要注意的是这里是-9,是3的平方,要设a倍的时候记得注意为3
21.
若m是分子中的最高次幂,n是分母中最高次幂,当n-m>1时,用倒代换90%成功
原本答案最后一步写的比较跳跃,我这里展开写了,应该不会觉得突兀了
22.
![]()
遇到这种题型呢,看分母有个很明显的特征,n次多项式,一般有两种思路,能因式分解就因式分解,不能的话只能凑完全平方公式然后用基本积分公式来求解,分母比分子的次数要大于1阶,所以可以用倒代换来进行求解
23.
一题多解是我向往喜欢的理想题型,这个题目就很典型,你也可以选择整体替换,你也可以三角代换,希望大家能灵活运用方法
24.
遇到根号,里面的项无法因式分解(a²-b²=(a+b)(a-b)),所以只能凑完全平方公式(a±b)²=a²±2ab+b²,然后凑基本积分求解即可,这个题另外的一个特点是分母的次数较高,也可以尝试倒代换,这个题目也很好
25.
这个题的确有点难想,我跟你分享一下我怎么想的,首先没法换元,可以考虑根式替换,但这个题有个更显著的特点,你看复合函数部分,(1+cosx)'=-sinx,假如分子要是也有个sinx就好了,那就分子分母同时乘以sinx,那分母的sin²x该怎么办怎么处理啊!别忘了一个最基本的公式sin²x+cos²x=1,那么推出sin²x=1-cos²x,还有后面的√1+cosx=u,那么推出cosx=u²-1,遇到cos²x直接替换即可,可能还有小伙伴不会因式分解的,这个需要自己在下面补习了
26.
不仅可以倒代换,三角代换,如果遇见指数较多的情况还可以指数代换,效果也不错
那么把指数替换的一些技巧放在下面以供参考
27.
这个题相较于前面的指数替换要稍微复杂一些,用了两次替换然后求解更容易一些题型Ⅲ—利用分部积分法求不定积分
解题思路:(1)首先要将它写成∫udv(或∫uv'dx)的形式
(2)多次应用分部积分法,每分部积分一次得以简化,直至最后求出。
(3)用分部积分法有时可导出∫f(x)dx的方程,然后解出。
(4)有时用分部积分法可导出递推公式
28.
本题属于典型的用分部积分法,因为标志是被积函数中
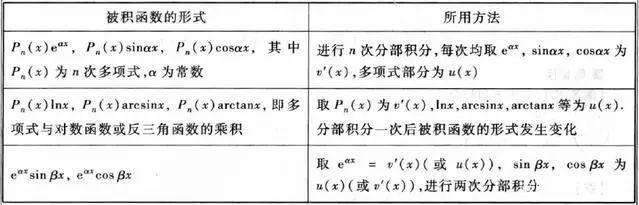
还记得分部积分法确定U的口诀吗?对了,反对幂三指(指三)
当一个被积函数中出现三角函数和指数函数的时候是同一优先级
可以看我下方的文章链接,还有表格法,相信你已经想到了
分部积分法(指三or三指)(可点击跳转至该文章)
分部积分法—公式法与表格法的终极对决(可点击跳转至该文章)
分部积分法之表格法(可点击跳转至该文章)
![]()
该题目的表格法如上
29.
这个题看着是蛮多项的哈,其实你也可以按乘法分配律一个个展开,然后相当于算三个小的不定积分题目,其实我觉得拆开更简单一点吧
30.
还是按照一般的套路,口诀,反对幂三指,这个被积函数里只有幂函数和反三角函数,因此反三角函数当U,幂函数当V,然后对其化间即可
31.
这种题又是不定积分中的另一类题型,是回头积分型,也就是说积着积着等号两边出现相同的部分,此时一定要注意不要不看你算的,一直循环下去就没完没了了,移项到等号的一边除以系数即可求解,不熟悉这套路的话我再给你举个例子,如下题
32.
相信你上面的那个题如果会的话,这个题也应该不在话下啦哈哈哈
这虽然并不是看起来表面上有两种函数,但你知道的其实相当于已经凑好了
旧文新发--分部积分法(可点击跳转至该文章)
如果对分部积分法不是那么了解,可点击本篇文章里有详细介绍,还有视频
33.
这个题的要点在于如何处理sin2x,高中的时候我们背过一个公式
叫做sin2x=2sinxcosx,相信这个公式对你来说一定没有那么陌生
然后其实相当于把sinx当作t来运算了,熟练了就像这样不用设t了
34.
这个题遇到两项之和可以试着拆开分别积分,前面的题也有这样做的
还有分母1±cosx一定要条件反射想到半角公式,不用问为什么就是这样
35.
如果最后一步觉得突兀的话,那是因为用到了这个公式
所以啦公式,还是那句话不能死记硬背,我都没想起来要用
我是翻了翻书才发现,诶,回头还得从新推导一遍
题型Ⅳ—利用恒等变形的不定积分
解题思路:要熟记以下的公式以及常用的恒等变形
36.
这种题型需要你一上手来进行一个恒等变形然后求解,在上面我们也说过一种情况是令e^x=t来进行换元,具体问题具体分析
37.
![]()
这个题目你也可以按照下面专门一个类型叫做部分分式来进行求解,其实前三部用脱式除法就能完成,具体的做法看我文章后半部分的专门例子吧
38.
这个题按说可以用根式替换,看我下面的另外一种解法
39.
这个题突破点是arctan1/x,我们知道arctanx的导数是1/1+x^2,从这里下手应该会简单一些,剩下的就不用我说了,基本公式
40.
这个例子很入门也很经典,希望大家能通过这个栗子对恒等变换有一个深深的记忆
题型Ⅴ—有理函数的不定积分
解题思路:
第一步——首先观察分子与分母的最高次幂的大小,如果有必要请做除法。那什么情况下有必要呢?
若分子的最高次幂小于分母的最高次幂,那么你运气很好直接进入第二步。
若不是,就要进行多项式的除法,然后再进入第二步。
第二步——对分母进行因式分解,使用二次公式或者猜想一个根,然后再做除法,以便因式分解被积函数的分母。
第三步——分部,像之前的描述那样,分别写出带有未知常数的“分部”,写下来一个像这样的等式:被积函数=分部。
第四步——计算常数的值,把方程两边同时乘以分母,通过任一方法计算常数的值:(a)换掉x的值;(b)系数相等法;或者结合使用(a)和(b)两种方法,现在你能用几个有理函数的和来表示这个被积函数,这些有理函数可能是分子为常数,分母为线性函数的幂,或者分子为线性函数分母为二次函数。
第五步——求解分母为线性项次幂的积分,求解分母是线性函数次幂的积分,答案将会是对数形式或该线性项的负次幂。
第六步——对分母是二次函数的被积函数求积分,对于分母是二次函数且不能因式分解的被积函数求微分,先配方,再换元,然后把它尽可能分解为两个积分,前者会涉及对数,而第二个会涉及正切函数的反函数,如果仅仅有一个积分,它可能是对数形式又可能是正切函数的反函数形式,这个公式通常是非常实用的。
有的题目是不需要都要经历这六步,有时候可能直接跳到最后一步
感兴趣童鞋们可以做做
41.
这种题目,在于观察分子与分母的关系,例如差了哪些项,差了几倍,然后+n-n技巧,跟分子分母相消拆成若干个小式子分别求不定积分
42.
这个题看到分子和分母既不是差几项几倍的关系,不妨同乘同除一些东西会有不一样的效果,然后再用完全平方公式进行凑,最后基本积分公式解决
43.
遇到这种假分式(“分子最高次幂比分母要高的”),要用除法脱式计算把他拆成一个整式和一个真分式之和,具体的详细操作,我把文章链接放在下面,非常详细
有理函数积分的完整方法(可点击跳转)
只要你有耐心看相信你会看懂的,这种题型都是一个套路
44.
这个题目难度蛮大的,主要考的是分母的因式分解还有完全平方公式
45.
凡是三角函数都能用第二个方法万能公式来解,理论上
但实际上可能操作起来比较麻烦,到万不得已的时候不要用第二种方法
46.
分母因式分解,通过待定系数法确定各个项的式子,也可以设特殊值来求解未知项
47.
分子次数跟分母次数差一次,就能凑微分了,也可以分母因式分解,但可能比较麻烦
48.
分母是两项相乘,就直接拆开,然后平衡系数,并逐项求不定积分
49.
主要用的是倍角公式,然后逐项拆,再用万能角公式
50.
看到括号里的部分,然后+n-n,做好几次这个方法,逐项求不定积分
题型Ⅵ—含根式的不定积分解法
解题思路:
51.
把根式换成次幂的形式,有时会比直接换元法要简单些
52.
分母用完全平方公式,然后凑微分即可
53.
这个题目的做法跟上面的一样再用基本积分公式求得
54.
分子与分母差常数项+n-n,然后凑微分即可
55.
方法与上面同上
56.
分子与分母通分,然后拆项各自求不定积分
57.
令整个根号为t,然后再拆分各自求不定积分
58.
设整个根号为t,然后约分,然后+n-n
59.
分母+n-n,然后拆项用基本积分公式求解
60.
这个题跟59题的方法一样
题型Ⅶ—三角有理式的不定积分
61.
遇见1要想起来它的变形,然后各自求不定积分
62.
还是考虑1的变形,凑完全平方公式
63.
方法同上
64.
方法同上
65.
用被角公式与分子分母约分
66.
看到好几个三角函数相乘,用积化和差
67.
用倍角函数预处理,在各自求不定积分
68.
sin²x=1-cos²x,再各自求不定积分
69.
看见一大堆三角函数,可以用tanx万能公式求解即可
70.
cosx用基本积分公式换元成sinx,分子加项减项再拆项即可
71.
sinx用基本积分公式换元成cosx,分子加项减项再拆项即可
72.
分母都是四次方,用完全平方公式再用基本求解公式求解即可
题型Ⅷ—含反三角函数的不定积分
解题思路:一般设反三角函数为u换元即可
73.
看到反三角函数,然后又看到分母的a²-x²的标准形式
用x=cost进行替换即可化简即可
74.
还是一样,表面上一个函数,直接用分部积分法求解即可,然后遇到根号换元
75.
看到两个反三角函数,直接用分部积分法求解即可
76.
![]()
设反三角函数为u,然后反解即可
题型Ⅸ—抽象函数的不定积分
77.
观察复合函数用其他的项来求它
78.
观察整个式子既有导数又有次方,求解的时候稍微有点乱
习题部分
79.
凑微分然后用分部积分法求解
80.
这个题目不止一种解法,其他的算法各位再想想拓展一些思路
81.
观察(x+2)^-2的导数与(x+1)只差常数倍,然后用分部积分法求解即可
82.
用分部积分法求解即可
83.
还是分部积分法,诶,都是一个套路
84.
设次幂为换元然后再拆项求不定积分即可
85.
看见复合函数x-1然后再去换元各项求不定积分
86.
还是一样的步骤,求不定积分
87.
分母有理化,然后次幂相加各自求不定积分即可
88.
分母是两部分项相乘,然后再拆项
分别求不定积分
89.
![]()
用分部积分法,e^x宜放在dv部分,而另一因式比较繁琐,应该拆项化简
90.
貌似是一个函数,其实已经给你凑好了,直接用分部积分法求解即可
91.
遇到根号换元,然后tan²x=sec²x-1求解即可
92.
复合函数的部分复合的导数等于其余项,这个题目比较简单
93.
遇到被积函数中大部分项目都是指数函数,那就设指数函数为t,同时除以e^2x,再凑完全平方公式即可
94.
看到1,sin²x+cos²x=1,然后分子分母约分,以此类推循环
求导不能再拆为止
95.
遇到奇次幂然后乘开,各自用基本积分公式求解即可
96.
遇到根号换元,然后乘法分配律各自求不定积分
97.
把分母放到d的后面然后分部积分法
98.
看到复合函数部分,复合部分的导数等于剩余部分,然后用半角公式求解
99.
看到了根号要想起换元然后再用分部积分法求解再用+n-n
这个题目不是很难
100.
最后的这个题目是群里有人问的,网上的答案普遍不是很详细
这次我写了个完整版,相信会对你有所帮助
对文章有什么疑问或错误,欢迎与我一起讨论
如果觉得文章还不错,点个打赏分享再走吧
笔耕不辍,有你支持