【自然语言处理】条件随机场【Ⅰ】马尔可夫随机场
有任何的书写错误、排版错误、概念错误等,希望大家包含指正。
部分推导和定义相关的佐证资料比较少,供参考。讨论的过程中我会加入自己的理解,难免存在错误,欢迎大家讨论。
在阅读本篇之前建议先学习:
隐马尔可夫模型系列
最大熵马尔可夫模型
由于字数限制,分成五篇博客。
【自然语言处理】条件随机场【Ⅰ】马尔可夫随机场
【自然语言处理】条件随机场【Ⅱ】条件随机场概述
【自然语言处理】条件随机场【Ⅲ】条件随机场估计问题
【自然语言处理】条件随机场【Ⅳ】条件随机场学习问题
【自然语言处理】条件随机场【Ⅴ】条件随机场解码问题
1. 随机场
随机变量、随机过程、随机场的定义或概念比较抽象,但其实我们还是比较容易理解的。
随机变量:随机变量表示随机试验各种结果的实值单值函数。随机事件不论与数量是否直接有关,都可以数量化,即都能用数量化的方式表达。简单地说,随机变量是指随机事件的数量表现。离散型随机变量即在一定区间内变量取值为有限个或可数个;连续型随机变量即在一定区间内变量取值有无限个,或数值无法一一列举出来。
随机过程:随机过程 X ( t ) X(t) X(t) 是一组依赖于实参数 t t t 的随机变量, t t t 一般具有时间的含义。随机过程 { X ( t ) , t ∈ T } \{ X(t), t∈T \} {X(t),t∈T} 可能取值的全体所构成的集合称为此随机过程的状态空间,记作 S S S。 比如某商店在从时间 t 0 t_0 t0 到时间 t K t_K tK 这段时间内接待顾客的人数,就是依赖于时间 t t t 的一组随机变量,即随机过程。
随机场:随机场更像是随机过程的推广。随机场不再局限于标量的概念,而是可以采用高维向量作为所依赖的随机变量。一个简单的例子,二维网格上的四个点 ( 0 , 0 ) (0,0) (0,0)、 ( 0 , 2 ) (0,2) (0,2)、 ( 2 , 0 ) (2,0) (2,0) 和 ( 2 , 2 ) (2,2) (2,2),对应随机变量 X 1 X_1 X1、 X 2 X_2 X2、 X 3 X_3 X3 和 X 4 X_4 X4,每个随机变量取值的概率依赖于其相邻位置的取值。在理解上不妨认为随机场与随机过程为同义词。
2. 马尔可夫随机场
概率无向图模型(probabilistic undirected graphical model),又称为马尔可夫随机场(Markov Random Field,MRF)或马尔可夫网(Markov Network),是一组有马尔可夫性质的随机变量的联合概率分布模型。
无论是有向概率图模型还是无向概率图模型,都表示将⼀组变量上的联合概率分布分解为局部条件概率分布的乘积的⼀种分解⽅式。两类模型也都会定义一组条件独立性质,根据图进⾏分解的任何概率分布都必须满⾜这些条件独⽴性质。在这里,我们考虑使用无向图描述的概率图模型,即概率无向图模型,它表示一个分解方式,也表示一组条件独立关系。
马尔可夫随机场由一个无向图和定义于无向图上的势函数(poential functions)组成。图中的每个结点表示一个或一组随机变量,结点之间的边表示两个变量之间的依赖关系。势函数亦称“因子”(factor),是定义在变量子集上的非负实函数,主要用于定义概率分布函数。
2.1. 团与最大团
团与最大团的定义:无向图 G G G 中任何两个结点均有边连接的结点子集称为团(clique)。若 C C C 是无向图 G G G 的一个团,并且不能再加进任何一个 G G G 的结点使其成为一个更大的团,则称此 C C C 为最大团(maximal clique)。
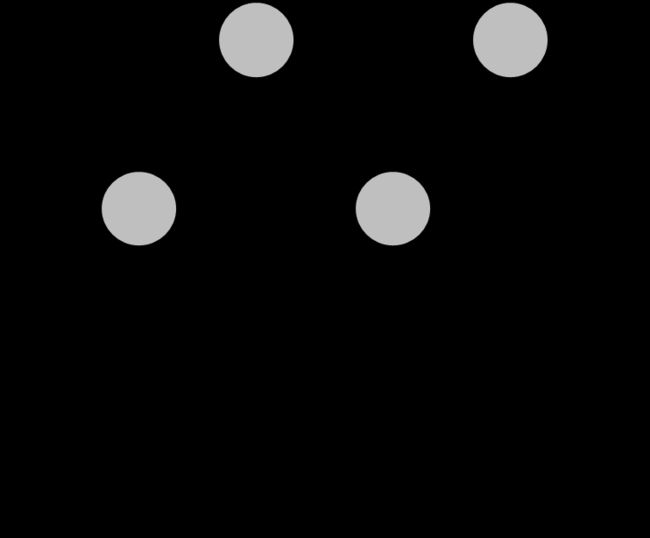
通俗来说,对于图中结点的一个子集,若其中任意两结点间都有边连接,则称该结点子集为一个团。若在一个团中加入另外任何一个结点都不再形成团,则称该团为最大团;换言之,最大团就是不能被其他团所包含的团。例如,在图 1 1 1 中, { x 1 , x 2 } \{x_1, x_2\} {x1,x2}, { x 1 , x 3 } \{x_1,x_3\} {x1,x3}, { x 2 , x 4 } \{x_2, x_4\} {x2,x4}, { x 2 , x 5 } \{x_2, x_5\} {x2,x5}, { x 2 , x 6 } \{x_2, x_6\} {x2,x6}, { x 3 , x 5 } \{x_3, x_5\} {x3,x5}, { x 5 , x 6 } \{x_5,x_6\} {x5,x6} 和 { x 2 , x 5 , x 6 } \{x_2, x_5, x_6\} {x2,x5,x6} 都是团,并且除了 { x 2 , x 5 } \{x_2,x_5\} {x2,x5}, { x 2 , x 6 } \{x_2,x_6\} {x2,x6} 和 { x 5 , x 6 } \{x_5,x_6\} {x5,x6} 之外都是最大团;但是,因为 x 2 x_2 x2 和 x 3 x_3 x3 之间缺乏连接, { x 1 , x 2 , x 3 } \{x_1,x_2,x_3\} {x1,x2,x3} 并不构成团。显然,每个结点至少出现在一个最大团中。
图 1 一个简单的马尔可夫随机场
2.2. 联合概率函数
将概率无向图模型的联合概率分布表示为其最大团上的随机变量的函数的乘积形式的操作,称为概率无向图模型的因子分解(factorization)。
具体来说,对于 n n n 个变量 x = { x 1 , x 2 , … , x n } {\rm x} = \{x_1, x_2,\dots, x_n\} x={x1,x2,…,xn},所有最大团构成的集合为 C \mathcal C C,与最大团 C ∈ C C∈\mathcal C C∈C 对应的变量集合记为 x C {\rm x}^{C} xC,则联合概率 P ( x ) P({\rm x}) P(x) 定义为
P ( x ) = 1 Z ∏ C ∈ C ψ C ( x C ) (1) P({\rm x}) = \frac{1}{Z} \prod_{C\in \mathcal C} \psi_C({\rm x}_C) \tag{1} P(x)=Z1C∈C∏ψC(xC)(1)
其中, Z Z Z 是规范化因子(normalization factor) ,由式
Z = ∑ x ∏ C ∈ C ψ C ( x C ) = ∑ x 1 , … , x n ∏ C ∈ C ψ C ( x C ) (2) Z = \sum_{\rm x} \prod_{C\in \mathcal C} \psi_C({\rm x}_C) = \sum_{x_1,\dots,x_n} \prod_{C\in \mathcal C} \psi_C({\rm x}_C) \tag{2} Z=x∑C∈C∏ψC(xC)=x1,…,xn∑C∈C∏ψC(xC)(2)
给出。规范化因子保证 P ( x ) P(\rm x) P(x) 是一个概率分布。函数 ψ C ( x C ) \psi_C({\rm x_C}) ψC(xC) 为势函数,通常定义为指数函数:
ψ C ( x C ) = exp ( − E C ( x C ) ) (3) \psi_C({\rm x}_C) = \exp(-E_C({\rm x}_C)) \tag{3} ψC(xC)=exp(−EC(xC))(3)
其中, E C ( x C ) E_C({\rm x}_C) EC(xC) 称为能量函数(energy function)。
对于图 1 1 1 的马尔可夫随机场,联合概率分布 P ( x ) P(\rm x) P(x) 定义为
P ( x ) = 1 Z ψ 12 ( x 1 , x 2 ) ψ 13 ( x 1 , x 3 ) ψ 24 ( x 2 , x 4 ) ψ 35 ( x 3 , x 5 ) ψ 256 ( x 2 , x 5 , x 6 ) P({\rm x}) = \frac{1}{Z} \psi_{12}(x_1,x_2)\psi_{13}(x_1,x_3)\psi_{24}(x_2,x_4)\psi_{35}(x_3,x_5)\psi_{256}(x_2,x_5,x_6) P(x)=Z1ψ12(x1,x2)ψ13(x1,x3)ψ24(x2,x4)ψ35(x3,x5)ψ256(x2,x5,x6)
关于马尔可夫随机场中的势函数,我们不把势函数的选择限制为具有具体概率含义(例如边缘概率分布或者条件概率分布)的函数。这与有向图的情形相反。在有向图的情形中,每个因⼦表示对应变量以它的父结点为条件的条件概率分布。当然,如果无向图是通过有向图去方向来构建的,那么势函数可能有具体意义。势函数的这一通用性导致它们的乘积无法直接表示概率分布,所以需要显式地引入规范化因子。
势函数 ψ C ( x C ) \psi_C({\rm x}_C) ψC(xC) 的作用是定量刻画变量集合 x C {\rm x}_C xC 中变量之间的相关关系,它应该是非负函数,且在所偏好的变量取值上有较大函数值。例如,假定图 1 1 1 中的变量均为二值变量,若部分势函数为
ψ 12 ( x 1 , x 2 ) = { 1.5 i f x 1 = x 2 0.1 o t h e r w i s e ψ 13 ( x 1 , x 3 ) = { 0.2 i f x 1 = x 3 1.3 o t h e r w i s e \psi_{12}(x_1,x_2) = \left\{ \begin{matrix} 1.5 & {\rm if} \space x_1= x_2 \\ 0.1 & {\rm otherwise} \end{matrix} \right.\\ \psi_{13}(x_1,x_3) = \left\{ \begin{matrix} 0.2 & {\rm if} \space x_1= x_3 \\ 1.3 & {\rm otherwise} \end{matrix} \right. ψ12(x1,x2)={1.50.1if x1=x2otherwiseψ13(x1,x3)={0.21.3if x1=x3otherwise
则说明该模型偏好变量 x 1 x_1 x1 与 x 2 x_2 x2 拥有相同的取值, x 1 x_1 x1 与 x 3 x_3 x3 拥有不同的取值;换言之,在该模型中 x 1 x_1 x1 与 x 2 x_2 x2 正相关, x 1 x_1 x1 与 x 3 x_3 x3 负相关。结合式 ( 1 ) (1) (1) 可知,令 x 1 x_1 x1 与 x 2 x_2 x2 相同且 x 1 x_1 x1 与 x 3 x_3 x3 不同的变量值指派将取得较高的联合概率。
能量函数 E C ( x C ) E_C({\rm x}_C) EC(xC) 是一个定义在变量 x C {\rm x}_C xC 上的实值函数,常见形式为
E C ( x C ) = ∑ i , j ∈ C , i ≠ j α i j x i x j + ∑ i ∈ Q β i x i E_C({\rm x}_C) = \sum_{i,j\in C,i\ne j} \alpha_{ij}x_ix_j+\sum_{i\in Q} \beta_i x_i EC(xC)=i,j∈C,i=j∑αijxixj+i∈Q∑βixi
其中 α i j \alpha_{ij} αij 和 β i \beta_i βi 是参数。上式中第一项考虑每一对结点的关系,第二项仅考虑单节点。
联合概率分布被定义为势函数的乘积,因此总能量 E ( x ) E(\rm x) E(x) 可以通过将每个最大团的能量相加的方法得到:
E ( x ) = ∑ C ∈ C E C ( x C ) (4) E({\rm x}) = \sum_{C\in \mathcal C} E_C({\rm x}_C)\tag{4} E(x)=C∈C∑EC(xC)(4)
用总能量 E ( x ) E(\rm x) E(x) 表示联合概率分布
P ( x ) = 1 Z exp ( − E ( x ) ) (5) P({\rm x}) = \frac{1}{Z}\exp(-E(\rm x))\tag{5} P(x)=Z1exp(−E(x))(5)
另外,还需要注意一点,规范化因子的存在使得无向图模型出现了一个严重的缺点。假设模型中的 n n n 个离散结点,每个结点有 m m m 个状态,根据 Z Z Z 的表达式可知, Z Z Z 的计算需要枚举全部结点的全部状态,即涉及到 m n m^n mn 个状态求和,因此(在最坏的情况下),计算量是模型大小的指数形式。对于参数学习来说,规范化因子是不可忽略的,因为规范化因子包含全部的势函数参数。但是,对于局部条件概率分布的计算,规范化因子是忽略的,因为条件概率可以通过两个边缘概率的比值计算出来,分子和分母的规范化因子可以被抵消。对于计算局部边缘概率,如果只涉及少量的变量,那么规范化因子的计算是可行的,比如计算 P ( { x 1 , x 2 , x 3 } ) P(\{x_1,x_2,x_3\}) P({x1,x2,x3}),假设每个结点有 2 2 2 个状态,根据规范化因子表达式可知,计算量为 2 3 = 8 2^3=8 23=8,这个计算量是非常小的。
举个例子来说明马尔可夫随机场的应用以及实践中如何定义势函数(或能量函数)。
以二值图像去噪为例,令观测的噪声图像通过⼀个⼆值像素值 y i ∈ { − 1 , + 1 } y_i\in \{-1,+1\} yi∈{−1,+1} 组成的数组来描述,其中下标 i = 1 , 2 , … , D i=1,2,\dots, D i=1,2,…,D 覆盖了所有像素。我们假设图像通过下⾯的⽅式获得:取⼀张未知的⽆噪声图像,这幅图像由⼆值像素值 x i ∈ { − 1 , + 1 } x_i\in \{-1,+1\} xi∈{−1,+1} 描述,然后以⼀个较小的概率随机翻转像素值的符号,噪声图像中像素值发⽣符号翻转的概率为 10 % 10\% 10%。给定带有噪声的图像,我们的目标是恢复原始的⽆噪声的图像。
由于噪声等级比较小,因此我们知道 x i x_i xi 和 y i y_i yi 之间有着强烈的相关性。我们还知道图像中相邻像素 x i x_i xi 和 x j x_j xj 的相关性很强。这种先验知识可以使用马尔科夫随机场模型进行描述,它的无向图如图 2 2 2 所示。
图 2 对应的无向图模型,灰色表示观测到的噪声图像中的像素,白色表示像素未知无噪声图像中的状态
图中的团数非常多,但是就两种类型,且均仅包含两个变量,这两类团分别为 { x i , y i } \{x_i,y_i\} {xi,yi} 和 { x i , x j } \{x_i,x_j\} {xi,xj},其中 i i i 和 j j j 为相邻像素下标。对于第一类团 { x i , y i } \{x_i,y_i\} {xi,yi},我们为这些团定义相同能量函数 − α x i y i -\alpha x_iy_i −αxiyi 来表达变量间的相关性,其中 α \alpha α 为正数。该能量函数的效果是:当 x i x_i xi 和 y i y_i yi 符号相同时,能量函数会给出一个较低的能量值,对应的势函数值较高;而当 x i x_i xi 和 y i y_i yi 符号相反时,能量函数会给出较高的能量值。另一类团 { x i , x j } \{x_i,x_j\} {xi,xj} 与第一类团一样,我们希望当两个像素符号相同时能量值较低,当两个像素符号相反时能量值较高,因此选择能量函数 − β x i x j -\beta x_ix_j −βxixj,其中 β \beta β 为正数。另外,由于势函数是最大团上的一个任意的非负函数,所以我们可以将势函数与团的子集上的任意非负函数相乘,或者等价地,我们可以加上对应的能量。在这个例子中,这使得我们可以为无噪声图像的每个像素 i i i 加上一个额外的项 γ x i \gamma x_i γxi,作用是使模型对于每个像素倾向于选择一个特定符号,而不选择另一个符号。于是,完整的总能量函数形式为
E ( x , y ) = γ ∑ i x i − α ∑ i x i y i − β ∑ { i , j } x i x j E({\rm x},{\rm y}) = \gamma \sum_{i} x_i - \alpha \sum_{i} x_iy_i - \beta\sum_{\{i,j\}}x_ix_j E(x,y)=γi∑xi−αi∑xiyi−β{i,j}∑xixj