机器学习教程篇2 -- K近邻(KNN)算法

    “学习如逆水行舟，不进则退”
    这一节开始讲KNN算法，说到这个算法，就不得不提到它的大表哥K-means算法，是不是觉得这两个家伙长得很像，其实他们区别还是挺大的。k近邻算法（knn）是一种基本的分类与回归的算法，k-means是一种基本的聚类方法。
    这一节讲KNN算法，下一节再讲K-means算法，并附上他们的对比。
    那我们开始吧！

k近邻算法（knn）

1、概念

    （1）K近邻(k-Nearest Neighbor，KNN)分类算法
            最简单的初级分类器，将全部训练数据所对应的类别记录下来，当测试对象的属性和某个训练对象完全匹配时，便对其进行分类。
            用官方的话来说，所谓K近邻算法，即是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例（也就是上面所说的K个邻居）， 这K个实例的多数属于某个类，就把该输入实例分类到这个类中。
    （2）算法思路：
            如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。
    （3）k近邻模型的三个基本要素：
            k值的选择：k值的选择会对结果产生重大影响。较小的k值可以减少近似误差，但是会增加估计误差；较大的k值可以减小估计误差，但是会增加近似误差。一般而言，通常采用交叉验证法来选取最优的k值。
            距离度量：距离反映了特征空间中两个实例的相似程度。可以采用欧氏距离、曼哈顿距离等。
            分类决策规则：往往采用多数表决。

2、举例说明

    如下图所示（图片来自百度百科），有两类不同的样本数据，分别用蓝色的小正方形和红色的小三角形表示，而图正中间的那个绿色的圆所标示的数据则是待分类的数据。也就是说，现在， 我们不知道中间那个绿色的数据是从属于哪一类（蓝色小正方形or红色小三角形），下面，我们就要解决这个问题：给这个绿色的圆分类。
    我们常说，物以类聚，人以群分，判别一个人是一个什么样品质特征的人，常常可以从他/她身边的朋友入手，所谓观其友，而识其人。我们不是要判别上图中那个绿色的圆是属于哪一类数据么，好说，从它的邻居下手。但一次性看多少个邻居呢？从图中，你还能看到：

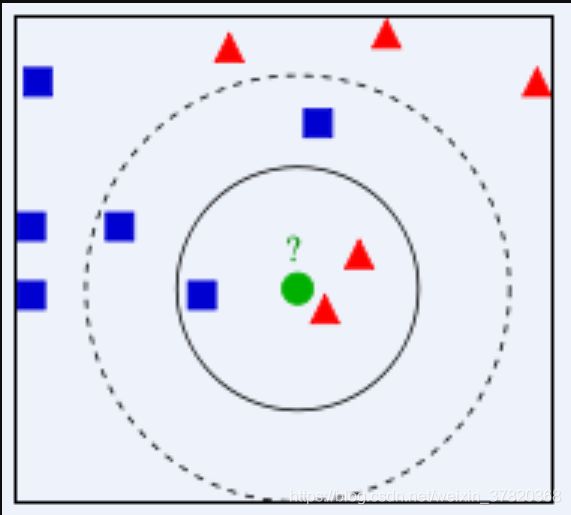
图片来自百度百科

    如果K=3，绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形，少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于红色的三角形一类。
    如果K=5，绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形，还是少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于蓝色的正方形一类。
    于此我们看到，当无法判定当前待分类点是从属于已知分类中的哪一类时，我们可以依据统计学的理论看它所处的位置特征，衡量它周围邻居的权重，而把它归为(或分配)到权重更大的那一类。这就是K近邻算法的核心思想。
    KNN算法的结果很大程度上取决于K的选择

3、KNN距离计算

    KNN中，通过计算对象间的距离作为各个对象之间非相似性指标，避免了对象之间的匹配问题，在这里距离一般采用欧氏距离或者曼哈顿距离：
    欧式距离(Euclidean distance)是通过直线距离(as the crow flies)来度量，即最短的直线路线。曼哈顿距离(anhattan distance)，即两点在南北方向上的距离加上在东西方向上的距离。
    下图中红线代表曼哈顿距离，绿线代表欧氏距离，蓝线和黄线代表等价的曼哈顿距离。

图片来自网络

    相应的公式如下：
    欧式距离：
$$d(x,y)=\sqrt{\sum _{k=1}^n(x_k-y_k{)}^2}$$
    曼哈顿距离：
$$d(x,y)=\sqrt{\sum _{k=1}^n|x_k-y_k|}$$

4、算法描述总结

    总结一下该算法的步骤：
    （1）计算测试数据与各个数据之间的距离；（公式已给）
    （2）按照距离的递增关系进行排序；（这一步相信大家也会）
    （3）选取距离最小的K个点；（K的大小由我们定义，对结果影响大）
    （4）确定前K个点所在类别出现的频率；
    （5）返回前K个点中出现频率最高的类别作为测试数据的预测分类。

5、代码

    网络上其实由很多案例教程，这里给出一份很简答的代码。

### 0.引入依赖
import numpy as np
import pandas as pd

#这里引入sklearn里的数据集，iris鸢尾花
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split# 切分数据集为训练集和测试集
from sklearn.metrics import accuracy_score #测试指标 计算分类预测的准确率

### 1. 数据加载和预处理
iris = load_iris()
df = pd.DataFrame(data = iris.data, columns = iris.feature_names)
df['class'] = iris.target
df['class'] = df['class'].map({0: iris.target_names[0], 1: iris.target_names[1], 2: iris.target_names[2]})
df.describe()

x = iris.data
#  x #(150，4),150行4列，每一行是个特征值，但是还是（-1，1）这种格式
y = iris.target.reshape(-1, 1)
print(x.shape, y.shape)

# 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=35, stratify=y)

print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)

### 2.核心算法实现
#距离函数定义
def l1_distance(a, b):
    return np.sum(np.abs(a-b), axis=1)
def l2_distance(a, b):
    return np.sqrt(np.sum((a-b)**2, axis=1))

#分类器实现
class KNN(object):
    def __init__(self, n_neighbors = 1, dist_func = l1_distance):
        self.n_neighbors = n_neighbors
        self.dist_func = dist_func
        
    # 训练模型方法
    def fit(self, x, y):
        self.x_train = x
        self.y_train = y
        
    # 模型预测方法
    def predict(self, x):
        # 初始化预测分类数组
        y_pred = np.zeros( (x.shape[0], 1), dtype=self.y_train.dtype)
        
        # 遍历输入的x数据点，取出每一个数据点的序号i和数据x_test
        for i, x_test in enumerate(x):
            # 一次循环其实只取出了一个点，x_test在跟所有的训练数据计算距离
            distances = self.dist_func(self.x_train, x_test)
            
            # 得到的距离按照从近到远排序，取出索引值
            nn_index = np.argsort(distances)
            '''
            ([0, 5, 100 ...])
            '''
            
            #选取最近范围的的K个点，保存他们对应的分类类别
            #这里并不是说distances就小，而是随机截取几个点，表示K截取范围
            nn_y = self.y_train[ nn_index[: self.n_neighbors] ].ravel()
            
            # 统计类别中出现频率最高那个，赋给y_pred[i]
            # 这里的argmax函数和bincount函数结合得很巧妙，可以记录一下
            y_pred[i] = np.argmax( np.bincount(nn_y) )
            
        return y_pred
    
### 3.测试
# 定义一个knn实例
knn = KNN(n_neighbors = 3)
# 训练模型
knn.fit(x_train, y_train)
# 传入测试数据，做预测
y_pred = knn.predict(x_test)

print(y_test.ravel())
print(y_pred.ravel())

# 求出预测准确率
accuracy = accuracy_score(y_test, y_pred)

print("预测准确率: ", accuracy)
# 定义一个knn实例
knn = KNN()
# 训练模型
knn.fit(x_train, y_train)

# 保存结果list
result_list = []

#针对不同的参数选取，做预测
for p in [1, 2]:
    knn.dist_func = l1_distance if p == 1 else l2_distance
    
    # 考虑不同的K取值，步长为2
    for k in range(1, 10, 2):
        knn.n_neighbors = k
        # 传入测试数据，做测试
        y_pred = knn.predict(x_test)
        # 求出预测的准确率
        accuracy = accuracy_score(y_test, y_pred)
        result_list.append([k, 'l1_distance' if p == 1 else 'l2_distance', accuracy])
    
df = pd.DataFrame(result_list, columns=['k', '距离函数', '准确率'])
df

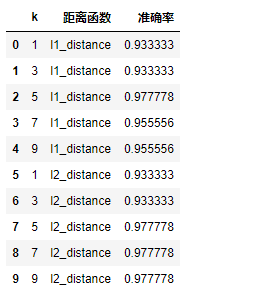
小结：knn其实就是没有训练，直接做测试的模型，自己定义一个范围作为划分的范围
代码更新：https://github.com/BZQLin/Linear-regression