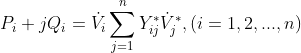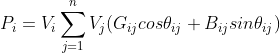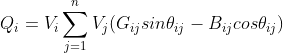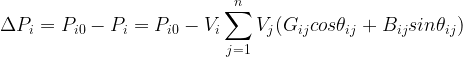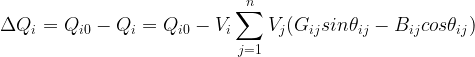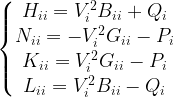牛顿法和P-Q分解法IEEE14系统潮流计算(附matlab代码)
目录
一、概述
二、潮流计算的数学模型
1.节点的分类
2.潮流计算方程
三、极坐标形式的牛顿法潮流计算(附matlab代码)
1.数据输入和导纳矩阵计算
2.求节点注入功率的不平衡量
3.求雅可比矩阵,解修正方程
4.修正节点电压
5.求支路功率
6.主函数
7.运行结果与matpower对比
四、P-Q分解法的潮流计算
一、概述
潮流计算是电力系统中最基本,应用最广泛的一种计算,是电力系统稳定计算和故障分析的基础。本文主要介绍极坐标下牛顿法和P-Q分解法的原理以及matlab实现,适用IEEE14节点系统进行测试,计算结果和应用matpower的潮流计算完全一致。
二、潮流计算的数学模型
1.节点的分类
按照潮流计算中给定的量不同,节点可分为以下三类:
(1)PQ节点:有功功率P和无功功率Q是给定的,一般负荷都是PQ节点;
(2)PV节点:有功功率P和电压幅值V是给定的;
(3)平衡节点:电压幅值V和相位角θ是给定的,系统中只有一个平衡节点。
2.潮流计算方程
加*表示取共轭,加·表示向量,其中Pi和Qi表示节点注入功率,Vi表示节点电压,Yij表示导纳矩阵中的元素。为了简化计算,可以将导纳矩阵分成实部和虚部,如下式:
![]()
另外,将节点电压用极坐标形式表示,如下:
![]()
这样就可以用导纳矩阵和节点电压表示节点的注入功率:
![]()
潮流计算的结果还需满足一定的约束条件,如节点电压上下限约束,发电机注入功率上下限约束,节点之间的相角差约束,支路功率约束等等。
另外,在求出节点电压和节点注入功率后,还需要求支路的传输功率,计算公式如下:
![]()
其中,Sij表示节点i到节点j的传输功率,yi0表示节点i的接地导纳,yij表示节点i和节点j之间的支路导纳。
三、极坐标形式的牛顿法潮流计算(附matlab代码)
牛顿法是常用的求解非线性方程的迭代方法,用于电力系统潮流计算时有直角坐标和极坐标两种迭代形式,本文以极坐标形式为例进行原理说明。具体步骤如下:
1.数据输入和导纳矩阵计算
输入电力系统节点、支路、发电机的基本参数,形成导纳矩阵;本文选用IEEE14节点进行测试,matlab代码如下:
IEEE14.m:
function mpc = IEEE14
mpc.version = '2';
%% system MVA base
mpc.baseMVA = 100;
%% bus data
% bus_i type Pd Qd Gs Bs area Vm Va baseKV zone Vmax Vmin
mpc.bus = [
1 3 0 0 0 0 1 1.06 0 0 1 1.06 0.94;
2 2 21.7 12.7 0 0 1 1.045 -4.98 0 1 1.06 0.94;
3 2 94.2 19 0 0 1 1.01 -12.72 0 1 1.06 0.94;
4 1 47.8 -3.9 0 0 1 1.019 -10.33 0 1 1.06 0.94;
5 1 7.6 1.6 0 0 1 1.02 -8.78 0 1 1.06 0.94;
6 2 11.2 7.5 0 0 1 1.07 -14.22 0 1 1.06 0.94;
7 1 0 0 0 0 1 1.062 -13.37 0 1 1.06 0.94;
8 2 0 0 0 0 1 1.09 -13.36 0 1 1.06 0.94;
9 1 29.5 16.6 0 19 1 1.056 -14.94 0 1 1.06 0.94;
10 1 9 5.8 0 0 1 1.051 -15.1 0 1 1.06 0.94;
11 1 3.5 1.8 0 0 1 1.057 -14.79 0 1 1.06 0.94;
12 1 6.1 1.6 0 0 1 1.055 -15.07 0 1 1.06 0.94;
13 1 13.5 5.8 0 0 1 1.05 -15.16 0 1 1.06 0.94;
14 1 14.9 5 0 0 1 1.036 -16.04 0 1 1.06 0.94;
];
%% generator data
% bus Pg Qg Qmax Qmin Vg mBase status Pmax Pmin Pc1 Pc2 Qc1min Qc1max Qc2min Qc2max ramp_agc ramp_10 ramp_30 ramp_q apf
mpc.gen = [
1 232.4 -16.9 10 0 1.06 100 1 332.4 0 0 0 0 0 0 0 0 0 0 0 0;
2 40 42.4 50 -40 1.045 100 1 140 0 0 0 0 0 0 0 0 0 0 0 0;
3 0 23.4 40 0 1.01 100 1 100 0 0 0 0 0 0 0 0 0 0 0 0;
6 0 12.2 24 -6 1.07 100 1 100 0 0 0 0 0 0 0 0 0 0 0 0;
8 0 17.4 24 -6 1.09 100 1 100 0 0 0 0 0 0 0 0 0 0 0 0;
];
%% branch data
% fbus tbus r x b rateA rateB rateC ratio angle status angmin angmax
mpc.branch = [
1 2 0.01938 0.05917 0.0528 0 0 0 0 0 1 -360 360;
1 5 0.05403 0.22304 0.0492 0 0 0 0 0 1 -360 360;
2 3 0.04699 0.19797 0.0438 0 0 0 0 0 1 -360 360;
2 4 0.05811 0.17632 0.034 0 0 0 0 0 1 -360 360;
2 5 0.05695 0.17388 0.0346 0 0 0 0 0 1 -360 360;
3 4 0.06701 0.17103 0.0128 0 0 0 0 0 1 -360 360;
4 5 0.01335 0.04211 0 0 0 0 0 0 1 -360 360;
4 7 0 0.20912 0 0 0 0 0.978 0 1 -360 360;
4 9 0 0.55618 0 0 0 0 0.969 0 1 -360 360;
5 6 0 0.25202 0 0 0 0 0.932 0 1 -360 360;
6 11 0.09498 0.1989 0 0 0 0 0 0 1 -360 360;
6 12 0.12291 0.25581 0 0 0 0 0 0 1 -360 360;
6 13 0.06615 0.13027 0 0 0 0 0 0 1 -360 360;
7 8 0 0.17615 0 0 0 0 0 0 1 -360 360;
7 9 0 0.11001 0 0 0 0 0 0 1 -360 360;
9 10 0.03181 0.0845 0 0 0 0 0 0 1 -360 360;
9 14 0.12711 0.27038 0 0 0 0 0 0 1 -360 360;
10 11 0.08205 0.19207 0 0 0 0 0 0 1 -360 360;
12 13 0.22092 0.19988 0 0 0 0 0 0 1 -360 360;
13 14 0.17093 0.34802 0 0 0 0 0 0 1 -360 360;
];
系统数据直接用matpower里的数据,方便进行结果的对比,计算导纳矩阵懒得写,直接用的matpower工具箱里的子函数:
function [Ybus, Yf, Yt] = creat_Y(baseMVA, bus, branch)
if nargin < 3
mpc = baseMVA;
baseMVA = mpc.baseMVA;
bus = mpc.bus;
branch = mpc.branch;
end
nb = size(bus, 1); %% number of buses
nl = size(branch, 1); %% number of lines
%% define the indices
BUS_I = 1; %% bus number (1 to 29997)
GS = 5; %% Gs, shunt conductance (MW at V = 1.0 p.u.)
BS = 6; %% Bs, shunt susceptance (MVAr at V = 1.0 p.u.)
F_BUS = 1; %% f, from bus number
T_BUS = 2; %% t, to bus number
BR_R = 3; %% r, resistance (p.u.)
BR_X = 4; %% x, reactance (p.u.)
BR_B = 5; %% b, total line charging susceptance (p.u.)
TAP = 9; %% ratio, transformer off nominal turns ratio
SHIFT = 10; %% angle, transformer phase shift angle (degrees)
BR_STATUS = 11; %% initial branch status, 1 - in service, 0 - out of service
if any(bus(:, BUS_I) ~= (1:nb)')
error('makeYbus: buses must be numbered consecutively in bus matrix; use ext2int() to convert to internal ordering')
end
stat = branch(:, BR_STATUS); %% ones at in-service branches
Ys = stat ./ (branch(:, BR_R) + 1j * branch(:, BR_X)); %% series admittance
Bc = stat .* branch(:, BR_B); %% line charging susceptance
tap = ones(nl, 1); %% default tap ratio = 1
i = find(branch(:, TAP)); %% indices of non-zero tap ratios
tap(i) = branch(i, TAP); %% assign non-zero tap ratios
tap = tap .* exp(1j*pi/180 * branch(:, SHIFT)); %% add phase shifters
Ytt = Ys + 1j*Bc/2;
Yff = Ytt ./ (tap .* conj(tap));
Yft = - Ys ./ conj(tap);
Ytf = - Ys ./ tap;
Ysh = (bus(:, GS) + 1j * bus(:, BS)) / baseMVA; %% vector of shunt admittances
f = branch(:, F_BUS); %% list of "from" buses
t = branch(:, T_BUS); %% list of "to" buses
if nb < 300 || have_feature('octave') %% small case OR running on Octave
i = [1:nl 1:nl]'; %% double set of row indices
Yf = sparse(i, [f; t], [Yff; Yft], nl, nb);
Yt = sparse(i, [f; t], [Ytf; Ytt], nl, nb);
Ybus = sparse([f;f;t;t], [f;t;f;t], [Yff;Yft;Ytf;Ytt], nb, nb) + ... %% branch admittances
sparse(1:nb, 1:nb, Ysh, nb, nb); %% shunt admittance
else %% large case running on MATLAB
Cf = sparse(1:nl, f, ones(nl, 1), nl, nb); %% connection matrix for line & from buses
Ct = sparse(1:nl, t, ones(nl, 1), nl, nb); %% connection matrix for line & to buses
Yf = sparse(1:nl, 1:nl, Yff, nl, nl) * Cf + sparse(1:nl, 1:nl, Yft, nl, nl) * Ct;
Yt = sparse(1:nl, 1:nl, Ytf, nl, nl) * Cf + sparse(1:nl, 1:nl, Ytt, nl, nl) * Ct;
Ybus = Cf' * Yf + Ct' * Yt + ... %% branch admittances
sparse(1:nb, 1:nb, Ysh, nb, nb); %% shunt admittance
end
2.求节点注入功率的不平衡量
假设系统共有n个节点,m个PQ节点,因为平衡节点有且只有一个,所以PV节点共有n-m-1个,对于所有的PQ节点和PV节点,可以列写有功功率的不平衡量方程:
对于PQ节点,还可以列写无功功率不平衡量的方程:
加起来一共有n-1-m个方程,和未知数的数量相同。对应的子函数如下:
function [ dP,dQ,Pi,Qi] = Unbalanced( n,m,P,Q,U,G,B,cita )
%计算ΔPi有功的不平衡量
for i=1:n
for j=1:n
Pn(j)=U(i)*U(j)*(G(i,j)*cos(cita(i)-cita(j))+B(i,j)*sin(cita(i)-cita(j)));
end
Pi(i)=sum(Pn);
end
dP=P(1:n-1)-Pi(1:n-1); %dP有n-1个
%计算ΔQi无功的不平衡量
for i=1:n
for j=1:n
Qn(j)=U(i)*U(j)*(G(i,j)*sin(cita(i)-cita(j))-B(i,j)*cos(cita(i)-cita(j)));
end
Qi(i)=sum(Qn);
end
dQ=Q(1:m)-Qi(1:m); %dQ有m个
end3.求雅可比矩阵,解修正方程
求雅可比矩阵之前,应先判断潮流计算是否满足收敛条件,如果满足则可以退出迭代,进一步计算支路潮流和平衡节点的功率,如果没有满足收敛条件则需要继续迭代。
极坐标表示的修正方程式如下:
其中,H是n-1阶方阵,N是(n-1)×m阶矩阵,K是m×(n-1)阶矩阵,K是m阶方阵
雅可比矩阵中各元素的计算公式如下:
当i≠j时:
当i=j时:
解修正方程,就可以得到节点电压的修正量。这部分对应的matlab代码如下:
% Jacobi: 计算雅可比矩阵
function [ J ] = Jacobi( n,m,U,cita,B,G,Pi,Qi )
%雅可比矩阵的计算
%分块 H N K L
%i!=j时
for i=1:n-1
for j=1:n-1
H(i,j)=-U(i)*U(j)*(G(i,j)*sin(cita(i)-cita(j))-B(i,j)*cos(cita(i)-cita(j)));
end
end
for i=1:n-1
for j=1:m
N(i,j)=-U(i)*U(j)*(G(i,j)*cos(cita(i)-cita(j))+B(i,j)*sin(cita(i)-cita(j)));
end
end
for i=1:m
for j=1:n-1
K(i,j)=U(i)*U(j)*(G(i,j)*cos(cita(i)-cita(j))+B(i,j)*sin(cita(i)-cita(j)));
end
end
for i=1:m
for j=1:m
L(i,j)=-U(i)*U(j)*(G(i,j)*sin(cita(i)-cita(j))-B(i,j)*cos(cita(i)-cita(j)));
end
end
%i==j时
for i=1:n-1
H(i,i)=U(i).^2*B(i,i)+Qi(i);
end
for i=1:m
N(i,i)=-U(i).^2*G(i,i)-Pi(i);
end
for i=1:m
K(i,i)=U(i).^2*G(i,i)-Pi(i);
end
for i=1:m
L(i,i)=U(i).^2*B(i,i)-Qi(i);
end
%合成雅可比矩阵
J=[H N;K L];
end
% function:求节点电压修正量
function [ dU,dcita ] = Correct( n,m,U,dP,dQ,J )
%求解节点电压修正量
for i=1:m
Ud2(i,i)=U(i);
end
dPQ=[dP dQ]';
dUcita=(-inv(J)*dPQ)';
dcita=dUcita(1:n-1);
dcita=[dcita 0];
dU=(Ud2*dUcita(n:n+m-1)')';
dU=[dU zeros(1,n-m)];
end4.修正节点电压
将各个节点的电压加上修正量,并返回第一步继续迭代。
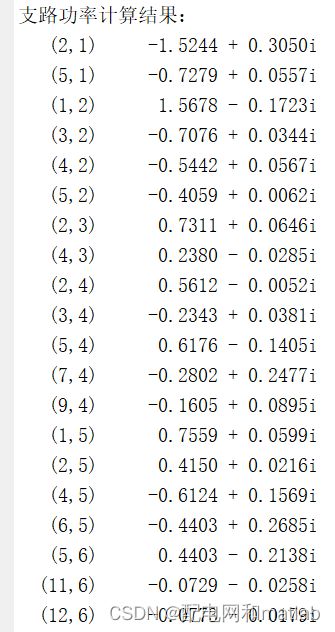
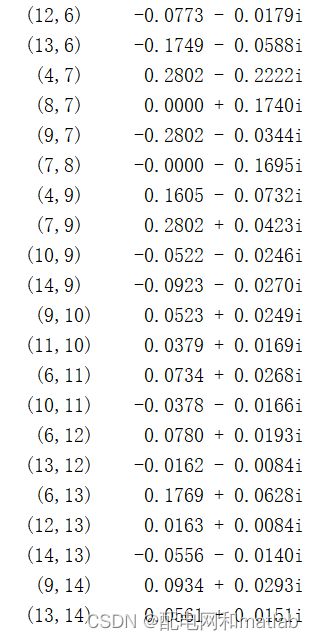
5.求支路功率
迭代完成后,还需要求出支路功率,计算公式在上文中已经介绍过了。这部分的matlab代码如下:
% line_power函数:用于计算支路功率
function Sij = line_power( n,y,U,cita )
for i=1:n
U1(i)=complex(U(i)*cos(cita(i)),U(i)*sin(cita(i)));
for j=1:n
U1(j)=complex(U(j)*cos(cita(j)),U(j)*sin(cita(j)));
Sij(i,j)=U1(i)*conj((U1(i)-U1(j))*y(i,j));
end
end
end6.主函数
clc
clear
%% 读取数据
mpc = IEEE14;
%% 初始化
%初始节点电压
[baseMVA,bus,gen,branch]=deal(mpc.baseMVA,mpc.bus,mpc.gen,mpc.branch);
n=14; %总节点数
m=9; %PQ节点数
P_load=bus(:,3);Q_load=bus(:,4);
P_gen=zeros(14,1);Q_gen=zeros(14,1);
for k=1:length(gen(:,1))
P_gen(gen(k,1))=gen(k,2);
Q_gen(gen(k,1))=gen(k,3);
end
P=zeros(1,n); %P,Q为原始数据,Pi,Qi为计算结果
Q=zeros(1,n);
for k=1:n
P(k)=P_gen(k)-P_load(k);
Q(k)=Q_gen(k)-Q_load(k);
end
[P,Q]=deal(P/baseMVA,Q/baseMVA);
U=bus(:,8)';%电压初始值由此确定
cita=bus(:,9)';%电压相角
cita=(deg2rad(cita)); %角度转换成弧度
show_index=input('是否在命令行展示计算过程?1-是,0-否');
%% 求导纳矩阵
Y=creat_Y(mpc);
G=real(Y);
B=imag(Y);
%% 计算功率不平衡量
[dP,dQ,Pi,Qi]=Unbalanced( n,m,P,Q,U,G,B,cita);
%% 迭代求解潮流
it=1;
it_max=50;
epr=0.001;%迭代收敛精度
if show_index==1
disp('初始条件:');disp('各节点有功:');disp(P);
disp('各节点无功:');disp(Q);
disp('各节点电压幅值:');disp(U);
cita=(deg2rad(cita)); %角度转换成弧度
disp('各节点电压相角(度):');disp(rad2deg(cita)); %显示依然使用角度
disp('节点导纳矩阵:');
disp(Y);
disp('有功不平衡量:');
disp(dP);
disp('无功不平衡量:');
disp(dQ);
end
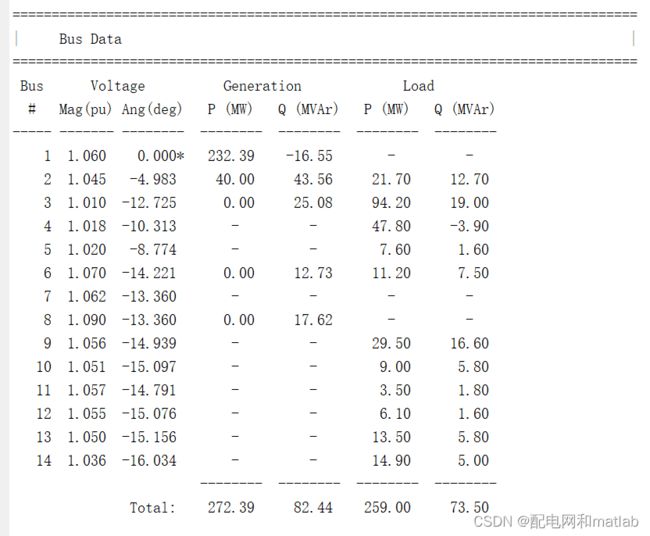
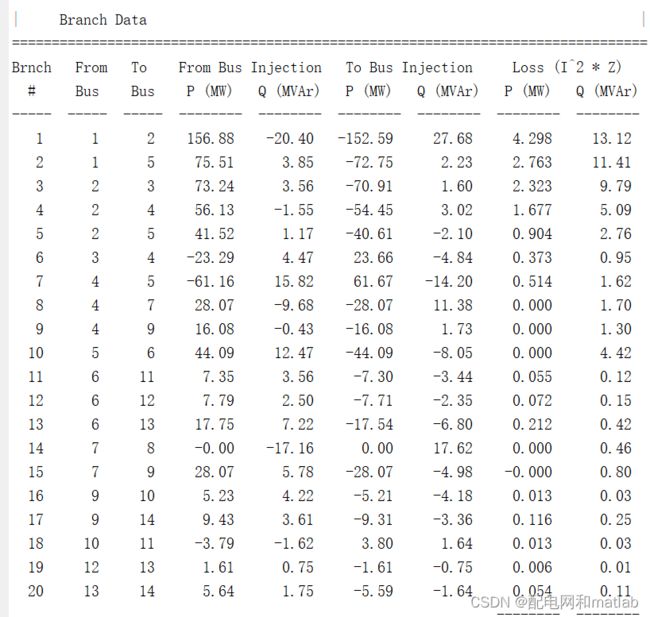
while it7.运行结果与matpower对比
代码运行的结果和matpower计算结果基本一致:
四、P-Q分解法的潮流计算
P-Q分解法是对牛顿法的改进,通过对极坐标形式的牛顿法的修正方程式进行简化,大大提升了计算速度,减少了内存占用量。基本原理如下:
在极坐标表示的牛顿法中,修正方程式如下:
其中,矩阵子块N和K一般都是很小的,与子块H、L相比可以忽略不计,因此,就可以把n-1+m阶的方程分解为一个n-1阶的方程和一个m阶的方程:
![]()
![]()
另外,一般情况下线路两端的相位角相差不大,而且由节点无功功率引起的导纳一般都远小于该节点自导纳的虚部,因此可以大致认为:
![]()
所以,矩阵H和L中的元素可以进一步简化:
![]()
![]()
由上述关系,修正方程式可以做进一步简化:
经过这样处理之后,修正方程的系数矩阵就变为了常数矩阵,只需要做一次三角分解,即可反复使用,结合稀疏矩阵的使用,可以进一步加快潮流计算的速度。
附:P-Q分解法的完整程序:电力系统潮流计算的matlab程序
参考资料:电力系统分析的计算机算法