可变多隐层神经网络的python实现

 

说明：这是我对网上代码的改写版本，目的是使它跟前一篇提到的使用方法尽量一致，用起来更直观些。

 

此神经网络有两个特点：

1、灵活性

非常灵活，隐藏层的数目是可以设置的，隐藏层的激活函数也是可以设置的

 

2、扩展性

扩展性非常好。目前只实现了一个学习方法：lm（Levenberg-Marquardt训练算法），你可以添加不同的学习方法到NeuralNetwork类

      什么是最优化，可分为几大类？
    答：Levenberg-Marquardt算法是最优化算法中的一种。最优化是寻找使得函数值最小的参数向量。它的应用领域非常广泛，如：经济学、管理优化、网络分析、最优设计、机械或电子设计等等。
    根据求导数的方法，可分为2大类。第一类，若f具有解析函数形式，知道x后求导数速度快。第二类，使用数值差分来求导数。
    根据使用模型不同，分为非约束最优化、约束最优化、最小二乘最优化。

      什么是Levenberg-Marquardt算法？
    答：它是使用最广泛的非线性最小二乘算法，中文为列文伯格-马夸尔特法。它是利用梯度求最大（小）值的算法，形象的说，属于“爬山”法的一种。它同时具有梯度法和牛顿法的优点。当λ很小时，步长等于牛顿法步长，当λ很大时，步长约等于梯度下降法的步长。

 

 （本文基于win7 + python3.4）

 

一、先说说改动的部分

1) 改写了NetStruct类初始化函数

原来：

1 class NetStruct: 
2     '''神经网络结构'''
3     def __init__(self, x, y, hidden_layers, activ_fun_list, performance_function = 'mse'):

 

现在：

1 class NetStruct: 
2     '''神经网络结构'''
3     def __init__(self, ni, nh, no, active_fun_list):
4         # ni 输入层节点数（int）
5         # ni 隐藏层节点数（int 或 list）
6         # no 输出层节点数（int）
7         # active_fun_list 隐藏层激活函数类型（list）

 

好处：

      初始化网络时更直观

 

2) 修改了NeuralNetwork类的train函数的参数

原来：

1 class NeuralNetwork:
2 
3     def __init__(self, ...):
4         # ...
5 
6     def train(self, method = 'lm'):
7         if(method == 'lm'):
8             self.lm()

 

现在：

 1 class NeuralNetwork:
 2     '''神经网络'''
 3     def __init__(self,  ...):
 4         '''初始化'''
 5         # ...
 6     
 7     def train(self, x, y, method = 'lm'):
 8         '''训练'''
 9         self.net_struct.x = x
10         self.net_struct.y = y
11         if(method == 'lm'):
12             self.lm()

 

好处：

      使用训练（train）函数时更直观

 

3) 修改了sinSamples样例函数的错误

　　原代码会报错："x与y维度不一致"

 

4) 添加了部分注释

      主要是为了更好地理解代码

 

 

 

二、再说说隐藏层的层数对误差的影响

效果图（peakSamples样例）

 

1) 两个隐藏层

 

误差：

100次迭代后，误差一般收敛在（1.3， 0.3）这个区间

 

 

2) 三个隐藏层

 

误差：

100次迭代后，误差一般收敛在（0.3， 0.1）这个区间

 

 结论：对于peakSamples这个样例，采用三个隐藏层优于两个隐藏层（显然，这里没有考虑与测试各隐藏层神经元数目改变的情况）

 

注：还可以试试另外一个测试函数

 

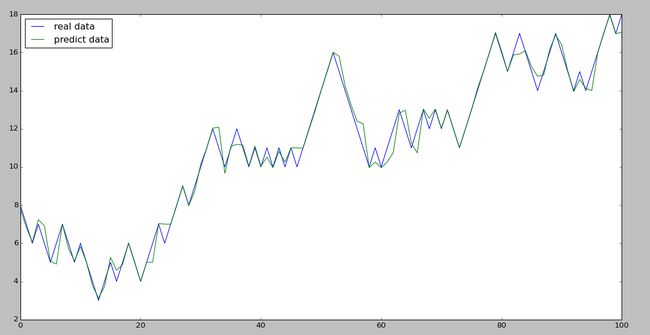
再附一个我用股票数据做的预测效果图 ：

 

 

完整代码：

  1 # neuralnetwork.py
  2 # modified by Robin 2015/03/03
  3 
  4 import numpy as np
  5 from math import exp, pow
  6 from mpl_toolkits.mplot3d import Axes3D
  7 import matplotlib.pyplot as plt
  8 import sys
  9 import copy
 10 from scipy.linalg import norm, pinv
 11 
 12 class Layer: 
 13     '''层'''
 14     def __init__(self, w, b, neure_number, transfer_function, layer_index):
 15         self.transfer_function = transfer_function
 16         self.neure_number = neure_number
 17         self.layer_index = layer_index
 18         self.w = w
 19         self.b = b
 20 
 21 class NetStruct: 
 22     '''神经网络结构'''
 23     def __init__(self, ni, nh, no, active_fun_list):
 24         # ni 输入层节点（int）
 25         # ni 隐藏层节点（int 或 list）
 26         # no 输出层节点（int）
 27         # active_fun_list 隐藏层激活函数类型（list）
 28         # ==> 1
 29         self.neurals = [] # 各层的神经元数目
 30         self.neurals.append(ni)
 31         if isinstance(nh, list):
 32             self.neurals.extend(nh)
 33         else:
 34             self.neurals.append(nh)
 35         self.neurals.append(no)
 36         # ==> 2
 37         if len(self.neurals)-2 == len(active_fun_list):
 38             active_fun_list.append('line')
 39         self.active_fun_list = active_fun_list
 40         # ==> 3
 41         self.layers = [] # 所有的层
 42         for i in range(0, len(self.neurals)):
 43             if i == 0:
 44                 self.layers.append(Layer([], [], self.neurals[i], 'none', i)) 
 45                 continue
 46             f = self.neurals[i - 1]
 47             s = self.neurals[i] 
 48             self.layers.append(Layer(np.random.randn(s, f), np.random.randn(s, 1), self.neurals[i], self.active_fun_list[i-1], i))
 49         
 50 class NeuralNetwork:
 51     '''神经网络'''
 52     def __init__(self, net_struct, mu = 1e-3, beta = 10, iteration = 100, tol = 0.1):
 53         '''初始化'''
 54         self.net_struct = net_struct
 55         self.mu = mu
 56         self.beta = beta
 57         self.iteration = iteration
 58         self.tol = tol
 59     
 60     def train(self, x, y, method = 'lm'):
 61         '''训练'''
 62         self.net_struct.x = x
 63         self.net_struct.y = y
 64         if(method == 'lm'):
 65             self.lm()
 66     
 67     def sim(self, x):
 68         '''预测'''
 69         self.net_struct.x = x
 70         self.forward()
 71         layer_num = len(self.net_struct.layers)
 72         predict = self.net_struct.layers[layer_num - 1].output_val
 73         return predict
 74     
 75     def actFun(self, z, active_type = 'sigm'):
 76         ''' 激活函数 '''
 77         # activ_type: 激活函数类型有 sigm、tanh、radb、line
 78         if active_type == 'sigm':
 79             f = 1.0 / (1.0 + np.exp(-z))
 80         elif active_type == 'tanh':
 81             f = (np.exp(z) + np.exp(-z)) / (np.exp(z) + np.exp(-z))
 82         elif active_type == 'radb':
 83             f = np.exp(-z * z)
 84         elif active_type == 'line':
 85             f = z
 86         return f
 87     
 88     def actFunGrad(self, z, active_type = 'sigm'):
 89         '''激活函数的变化（派生）率'''
 90         # active_type: 激活函数类型有 sigm、tanh、radb、line
 91         y = self.actFun(z, active_type)
 92         if active_type == 'sigm':
 93             grad = y * (1.0 - y)
 94         elif active_type == 'tanh':
 95             grad = 1.0 - y * y
 96         elif active_type == 'radb':
 97             grad = -2.0 * z * y
 98         elif active_type == 'line':
 99             m = z.shape[0]
100             n = z.shape[1]
101             grad = np.ones((m, n))
102         return grad
103     
104     def forward(self): 
105         ''' 前向 '''
106         layer_num = len(self.net_struct.layers)
107         for i in range(0, layer_num):
108             if i == 0:
109                 curr_layer = self.net_struct.layers[i]
110                 curr_layer.input_val = self.net_struct.x
111                 curr_layer.output_val = self.net_struct.x
112                 continue
113             before_layer = self.net_struct.layers[i - 1]
114             curr_layer = self.net_struct.layers[i]
115             curr_layer.input_val = curr_layer.w.dot(before_layer.output_val) + curr_layer.b
116             curr_layer.output_val = self.actFun(curr_layer.input_val, 
117                                                 self.net_struct.active_fun_list[i - 1])
118     
119     def backward(self):
120         '''反向'''
121         layer_num = len(self.net_struct.layers)
122         last_layer = self.net_struct.layers[layer_num - 1]
123         last_layer.error = -self.actFunGrad(last_layer.input_val,
124                                             self.net_struct.active_fun_list[layer_num - 2])
125         layer_index = list(range(1, layer_num - 1)) 
126         layer_index.reverse()
127         for i in layer_index:
128             curr_layer = self.net_struct.layers[i]
129             curr_layer.error = (last_layer.w.transpose().dot(last_layer.error)) * self.actFunGrad(curr_layer.input_val,self.net_struct.active_fun_list[i - 1])
130             last_layer = curr_layer
131     
132     def parDeriv(self):
133         '''标准梯度（求导）'''
134         layer_num = len(self.net_struct.layers)
135         for i in range(1, layer_num):
136             befor_layer = self.net_struct.layers[i - 1]
137             befor_input_val = befor_layer.output_val.transpose()
138             curr_layer = self.net_struct.layers[i]
139             curr_error = curr_layer.error
140             curr_error = curr_error.reshape(curr_error.shape[0]*curr_error.shape[1], 1, order='F')
141             row =  curr_error.shape[0]
142             col = befor_input_val.shape[1]
143             a = np.zeros((row, col))
144             num = befor_input_val.shape[0]
145             neure_number = curr_layer.neure_number
146             for i in range(0, num):
147                 a[neure_number*i:neure_number*i + neure_number,:] = np.repeat([befor_input_val[i,:]],neure_number,axis = 0)
148             tmp_w_par_deriv = curr_error * a
149             curr_layer.w_par_deriv = np.zeros((num, befor_layer.neure_number * curr_layer.neure_number))
150             for i in range(0, num):
151                 tmp = tmp_w_par_deriv[neure_number*i:neure_number*i + neure_number,:]
152                 tmp = tmp.reshape(tmp.shape[0] * tmp.shape[1], order='C')
153                 curr_layer.w_par_deriv[i, :] = tmp
154                 curr_layer.b_par_deriv = curr_layer.error.transpose()
155     
156     def jacobian(self):
157         '''雅可比行列式'''
158         layers = self.net_struct.neurals
159         row = self.net_struct.x.shape[1]
160         col = 0
161         for i in range(0, len(layers) - 1):
162             col = col + layers[i] * layers[i + 1] + layers[i + 1]
163         j = np.zeros((row, col))
164         layer_num = len(self.net_struct.layers)
165         index = 0
166         for i in range(1, layer_num):
167             curr_layer = self.net_struct.layers[i]
168             w_col = curr_layer.w_par_deriv.shape[1]
169             b_col = curr_layer.b_par_deriv.shape[1]
170             j[:, index : index + w_col] = curr_layer.w_par_deriv
171             index = index + w_col
172             j[:, index : index + b_col] = curr_layer.b_par_deriv
173             index = index + b_col
174         return j
175     
176     def gradCheck(self):
177         '''梯度检查'''
178         W1 = self.net_struct.layers[1].w
179         b1 = self.net_struct.layers[1].b
180         n = self.net_struct.layers[1].neure_number
181         W2 = self.net_struct.layers[2].w
182         b2 = self.net_struct.layers[2].b
183         x = self.net_struct.x
184         p = []
185         p.extend(W1.reshape(1,W1.shape[0]*W1.shape[1],order = 'C')[0])
186         p.extend(b1.reshape(1,b1.shape[0]*b1.shape[1],order = 'C')[0])
187         p.extend(W2.reshape(1,W2.shape[0]*W2.shape[1],order = 'C')[0])
188         p.extend(b2.reshape(1,b2.shape[0]*b2.shape[1],order = 'C')[0])
189         old_p = p
190         jac = []
191         for i in range(0, x.shape[1]):
192             xi = np.array([x[:,i]])
193             xi = xi.transpose()
194             ji = []
195             for j in range(0, len(p)):
196                 W1 = np.array(p[0:2*n]).reshape(n,2,order='C')
197                 b1 = np.array(p[2*n:2*n+n]).reshape(n,1,order='C')
198                 W2 = np.array(p[3*n:4*n]).reshape(1,n,order='C')
199                 b2 = np.array(p[4*n:4*n+1]).reshape(1,1,order='C')
200 
201                 z2 = W1.dot(xi) + b1
202                 a2 = self.actFun(z2)
203                 z3 = W2.dot(a2) + b2
204                 h1 = self.actFun(z3)
205                 p[j] = p[j] + 0.00001
206                 W1 = np.array(p[0:2*n]).reshape(n,2,order='C')
207                 b1 = np.array(p[2*n:2*n+n]).reshape(n,1,order='C')
208                 W2 = np.array(p[3*n:4*n]).reshape(1,n,order='C')
209                 b2 = np.array(p[4*n:4*n+1]).reshape(1,1,order='C')
210 
211                 z2 = W1.dot(xi) + b1
212                 a2 = self.actFun(z2)
213                 z3 = W2.dot(a2) + b2
214                 h = self.actFun(z3)
215                 g = (h[0][0]-h1[0][0])/0.00001
216                 ji.append(g)
217             jac.append(ji)
218             p = old_p
219         return jac
220     
221     def jjje(self):
222         '''计算jj与je'''
223         layer_num = len(self.net_struct.layers)
224         e = self.net_struct.y - self.net_struct.layers[layer_num - 1].output_val
225         e = e.transpose()
226         j = self.jacobian()
227         #check gradient
228         #j1 = -np.array(self.gradCheck())
229         #jk = j.reshape(1,j.shape[0]*j.shape[1])
230         #jk1 = j1.reshape(1,j1.shape[0]*j1.shape[1])
231         #plt.plot(jk[0])
232         #plt.plot(jk1[0],'.')
233         #plt.show()
234         jj = j.transpose().dot(j)
235         je = -j.transpose().dot(e)
236         return[jj, je]
237     
238     def lm(self):
239         '''Levenberg-Marquardt训练算法'''
240         mu = self.mu
241         beta = self.beta
242         iteration = self.iteration
243         tol = self.tol
244         y = self.net_struct.y
245         layer_num = len(self.net_struct.layers)
246         self.forward()
247         pred =  self.net_struct.layers[layer_num - 1].output_val
248         pref = self.perfermance(y, pred)
249         for i in range(0, iteration):
250             print('iter:',i, 'error:', pref)
251             #1) 第一步: 
252             if(pref < tol):
253                 break
254             #2) 第二步:
255             self.backward()
256             self.parDeriv()
257             [jj, je] = self.jjje()
258             while(1):
259                 #3) 第三步: 
260                 A = jj + mu * np.diag(np.ones(jj.shape[0]))
261                 delta_w_b = pinv(A).dot(je)
262                 #4) 第四步:
263                 old_net_struct = copy.deepcopy(self.net_struct)
264                 self.updataNetStruct(delta_w_b)
265                 self.forward()
266                 pred1 =  self.net_struct.layers[layer_num - 1].output_val
267                 pref1 = self.perfermance(y, pred1)
268                 if (pref1 < pref):
269                     mu = mu / beta
270                     pref = pref1
271                     break
272                 mu = mu * beta
273                 self.net_struct = copy.deepcopy(old_net_struct)
274     
275     def updataNetStruct(self, delta_w_b):
276         '''更新网络权重及阈值'''
277         layer_num = len(self.net_struct.layers)
278         index = 0
279         for i in range(1, layer_num):
280             before_layer = self.net_struct.layers[i - 1]
281             curr_layer = self.net_struct.layers[i]
282             w_num = before_layer.neure_number * curr_layer.neure_number
283             b_num = curr_layer.neure_number
284             w = delta_w_b[index : index + w_num]
285             w = w.reshape(curr_layer.neure_number, before_layer.neure_number, order='C')
286             index = index + w_num
287             b = delta_w_b[index : index + b_num]
288             index = index + b_num
289             curr_layer.w += w
290             curr_layer.b += b
291     
292     def perfermance(self, y, pred):
293         '''性能函数'''
294         error = y - pred
295         return norm(error) / len(y)
296 
297         
298         
299 # 以下函数为测试样例      
300 def plotSamples(n = 40):
301     x = np.array([np.linspace(0, 3, n)])
302     x = x.repeat(n, axis = 0)
303     y = x.transpose()
304     z = np.zeros((n, n))
305     for i in range(0, x.shape[0]):
306         for j in range(0, x.shape[1]):
307             z[i][j] = sampleFun(x[i][j], y[i][j])
308     fig = plt.figure()
309     ax = fig.gca(projection='3d')
310     surf = ax.plot_surface(x, y, z, cmap='autumn', cstride=2, rstride=2)
311     ax.set_xlabel("X-Label")
312     ax.set_ylabel("Y-Label")
313     ax.set_zlabel("Z-Label")
314     plt.show()
315 
316 def sinSamples(n):
317     x = np.array([np.linspace(-0.5, 0.5, n)])
318     #x = x.repeat(n, axis = 0)
319     y = x + 0.2
320     z = np.zeros((n, 1))
321     for i in range(0, x.shape[1]):
322         z[i] = np.sin(x[0][i] * y[0][i])
323     X = np.zeros((n, 2))
324     n = 0
325     for xi, yi in zip(x.transpose(), y.transpose()):
326         X[n][0] = xi
327         X[n][1] = yi
328         n = n + 1
329     # print(x.shape, y.shape)
330     # print(X.shape, z.shape)
331     return X, z.transpose()
332 
333 def peaksSamples(n):
334     x = np.array([np.linspace(-3, 3, n)])
335     x = x.repeat(n, axis = 0)
336     y = x.transpose()
337     z = np.zeros((n, n))
338     for i in range(0, x.shape[0]):
339         for j in range(0, x.shape[1]):
340             z[i][j] = sampleFun(x[i][j], y[i][j])
341     X = np.zeros((n*n, 2))
342     x_list = x.reshape(n*n,1 )
343     y_list = y.reshape(n*n,1)
344     z_list = z.reshape(n*n,1)
345     n = 0
346     for xi, yi in zip(x_list, y_list):
347         X[n][0] = xi
348         X[n][1] = yi
349         n = n + 1
350     # print(x.shape, y.shape)
351     # print(X.shape, z.shape, z_list.shape, z_list.transpose().shape)
352     return X,z_list.transpose()
353 
354 def sampleFun( x, y):
355     z =  3*pow((1-x),2) * exp(-(pow(x,2)) - pow((y+1),2))  - 10*(x/5 - pow(x, 3) - pow(y, 5)) * exp(-pow(x, 2) - pow(y, 2)) - 1/3*exp(-pow((x+1), 2) - pow(y, 2)) 
356     return z
357 
358 
359 
360 
361 # 测试
362 if __name__ == '__main__':
363 
364     active_fun_list = ['sigm','sigm','sigm']# 【必须】设置【各】隐层的激活函数类型，可以设置为tanh,radb，tanh,line类型，如果不显式的设置最后一层为line 
365     ns = NetStruct(2, [10, 10, 10], 1, active_fun_list) # 确定神经网络结构，中间两个隐层各10个神经元
366     nn = NeuralNetwork(ns) # 神经网络类实例化
367     
368     [X, z] = peaksSamples(20) # 产生训练数据
369     #[X, z] = sinSamples(20)  # 第二个训练数据
370     X = X.transpose()
371     
372     # 注意：测试数据的格式与我们习惯的用法有差别，行列要转置！！原因是内部逻辑采用了矩阵运算？！！！！
373     #print(X.shape) # (2, 20)
374     #print(X)
375     #print(z.shape) # (1, 20)
376     #print(z)
377     
378     nn.train(X, z) # 训练！！！！！！
379     
380     [X0, z0] = peaksSamples(40) # 产生测试数据
381     #[X0, z0] = sinSamples(40)  # 第二个测试数据
382     X0 = X0.transpose()
383     
384     z1 = nn.sim(X0) # 预测！！！！！！
385 
386     fig  = plt.figure()
387     ax = fig.add_subplot(111)
388     ax.plot(z0[0])      # 画出真实值 real data
389     ax.plot(z1[0],'r.') # 画出预测值 predict data
390     plt.legend(('real data', 'predict data'))
391     plt.show() 

 

转载于:https://www.cnblogs.com/hhh5460/p/4310083.html