Python机器学习基础教程

监督学习与预处理

在无监督学习中，学习算法只有输入数据，并需要从这些数据中提取知识。

无监督学习的类型

数据集变换

创建数据新的表示的算法，新的表示可以更容易被人或其他机器学习算法理解。常见的应用是降维，用较少的特征就可以概括数据的重要特征。无监督变换的另一个应用是找到构成数据的各个组成部分，对文本文档集合进行主题提取。

聚类

将数据划分成不同的组，每组包含相似的物项。

无监督学习的挑战

评估算法是否学习到了有用的东西。因为无监督算法一般用于不包含任何标签信息的数据，所以我们不知道正确的输出应该是什么，因此很难判断一个模型是否表现的很好。

预处理与缩放

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import mglearn

mglearn.plots.plot_scaling()

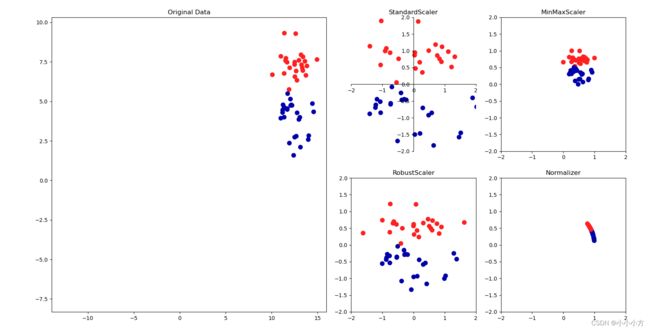
scikit-lear中的standardscaler确保每个特征的平均值为0，方差为1，使得所有特征都位于同一量级，但是这种缩放不能确保特征任何特丁的最大值和最小值。RobustScaler也是确保每个特征的统计属性都位于同一范围，但是使用的是中位数和四分位数，不是平均值和方差，会忽略与其他点有很大不同的数据点（异常值）。MinMaxScaler 移动数据，使得所有特征都刚好位于0到1之间。对于二维i数据集来说，所有的数据都包含在x轴0到1与y轴0到1组成的矩形中。Normalizer 用到一种完全不同的缩放方法，他对每个数据点进行缩放，使得特征向量的欧式长度等于1.它将一个数据点投射到半径为1的圆上（对于高维度的情况是球面）。这意味着每个数据点的缩放比例都不相同（乘以其长度的倒数）。如果只有数据的方向是重要的，特征的长度是无关紧要的，通常会使用这种归一化。

应用数据变换

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target,random_state=1)
print(X_train.shape)
print(X_test.shape)
# 导入预处理的类并将其实例化
from sklearn.preprocessing import MinMaxScaler
# 对于 MinMaxScaler 来说，fit 方法计算训练集中每个特征的最大值和最小值
scaler = MinMaxScaler()

# 使用fit拟合缩放器
scaler.fit(X_train)
# 每当模型返回数据的一种新表示时，都可以使用 transform方法
# 变换数据
X_train_scaled = scaler.transform(X_train)
# 在缩放之前和之后分别打印数据集属性
print("transformed shape: {}".format(X_train_scaled.shape))
print("per-feature minimum before scaling:\n {}".format(X_train.min(axis=0)))
print("per-feature maximum before scaling:\n {}".format(X_train.max(axis=0)))
print("per-feature minimum after scaling:\n {}".format(X_train_scaled.min(axis=0)))
print("per-feature maximum after scaling:\n {}".format(X_train_scaled.max(axis=0)))

运行结果：
(426, 30)
(143, 30)
transformed shape: (426, 30)
per-feature minimum before scaling:
 [6.981e+00 9.710e+00 4.379e+01 1.435e+02 5.263e-02 1.938e-02 0.000e+00
 0.000e+00 1.060e-01 5.024e-02 1.153e-01 3.602e-01 7.570e-01 6.802e+00
 1.713e-03 2.252e-03 0.000e+00 0.000e+00 9.539e-03 8.948e-04 7.930e+00
 1.202e+01 5.041e+01 1.852e+02 7.117e-02 2.729e-02 0.000e+00 0.000e+00
 1.566e-01 5.521e-02]
per-feature maximum before scaling:
 [2.811e+01 3.928e+01 1.885e+02 2.501e+03 1.634e-01 2.867e-01 4.268e-01
 2.012e-01 3.040e-01 9.575e-02 2.873e+00 4.885e+00 2.198e+01 5.422e+02
 3.113e-02 1.354e-01 3.960e-01 5.279e-02 6.146e-02 2.984e-02 3.604e+01
 4.954e+01 2.512e+02 4.254e+03 2.226e-01 9.379e-01 1.170e+00 2.910e-01
 5.774e-01 1.486e-01]
per-feature minimum after scaling:
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0.]
per-feature maximum after scaling:
 [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1.]

变换后的数据形状与原始数据相同，特征只是发生了移动和缩放。现在所有的特征都位于0和1之间。

# 对测试数据进行变换
X_test_scaled = scaler.transform(X_test)
# 在缩放之后打印测试数据的属性
print("per-feature minimum after scaling:\n{}".format(X_test_scaled.min(axis=0)))
print("per-feature maximum after scaling:\n{}".format(X_test_scaled.max(axis=0)))
运行结果：
per-feature minimum after scaling:
[ 0.0336031   0.0226581   0.03144219  0.01141039  0.14128374  0.04406704
  0.          0.          0.1540404  -0.00615249 -0.00137796  0.00594501
  0.00430665  0.00079567  0.03919502  0.0112206   0.          0.
 -0.03191387  0.00664013  0.02660975  0.05810235  0.02031974  0.00943767
  0.1094235   0.02637792  0.          0.         -0.00023764 -0.00182032]
per-feature maximum after scaling:
[0.9578778  0.81501522 0.95577362 0.89353128 0.81132075 1.21958701
 0.87956888 0.9333996  0.93232323 1.0371347  0.42669616 0.49765736
 0.44117231 0.28371044 0.48703131 0.73863671 0.76717172 0.62928585
 1.33685792 0.39057253 0.89612238 0.79317697 0.84859804 0.74488793
 0.9154725  1.13188961 1.07008547 0.92371134 1.20532319 1.63068851]

对测试集缩放后的最大值和最小值不是 1 和 0，这或许有些出乎意料。有些特征甚至在 0~1 的范围之外！对此的解释是MinMaxScaler（以及其他所有缩放器）总是对训练集和测试集应用完全相同的变换。也就是说，transform 方法总是减去训练集的最小值，然后除以训练集的范围，而这两个值可能与测试集的最小值和范围并不相同。

对训练数据和测试数据进行相同的缩放

为了让监督模型能够在测试集上运行，对训练集和测试集应用完全相同的变换是很重要的。

from sklearn.datasets import make_blobs
# 构造数据
X, _ = make_blobs(n_samples=50, centers=5, random_state=4, cluster_std=2)
# 将其分为训练集和测试集
X_train, X_test = train_test_split(X, random_state=5, test_size=.1)
# 绘制训练集和测试集
fig, axes = plt.subplots(1, 3, figsize=(13, 4))
axes[0].scatter(X_train[:, 0], X_train[:, 1],c=mglearn.cm2(0), label="Training set", s=60)
axes[0].scatter(X_test[:, 0], X_test[:, 1], marker='^',c=mglearn.cm2(1), label="Test set", s=60)
axes[0].legend(loc='upper left')
axes[0].set_title("Original Data")
# 利用MinMaxScaler缩放数据
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
# 将正确缩放的数据可视化
axes[1].scatter(X_train_scaled[:, 0], X_train_scaled[:, 1],c=mglearn.cm2(0), label="Training set", s=60)
axes[1].scatter(X_test_scaled[:, 0], X_test_scaled[:, 1], marker='^',c=mglearn.cm2(1), label="Test set", s=60)
axes[1].set_title("Scaled Data")
# 单独对测试集进行缩放
# 使得测试集的最小值为0，最大值为1
# 千万不要这么做！这里只是为了举例
test_scaler = MinMaxScaler()
test_scaler.fit(X_test)
X_test_scaled_badly = test_scaler.transform(X_test)
# 将错误缩放的数据可视化
axes[2].scatter(X_train_scaled[:, 0], X_train_scaled[:, 1],c=mglearn.cm2(0), label="training set", s=60)
axes[2].scatter(X_test_scaled_badly[:, 0], X_test_scaled_badly[:, 1],marker='^', c=mglearn.cm2(1), label="test set", s=60)
axes[2].set_title("Improperly Scaled Data")
for ax in axes:
    ax.set_xlabel("Feature 0")
    ax.set_ylabel("Feature 1")
plt.show()

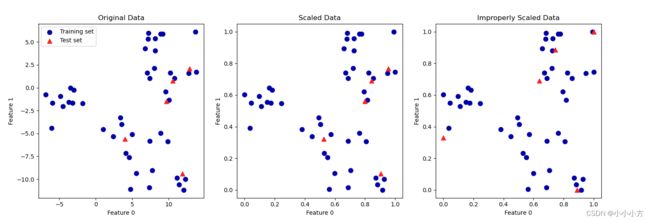
第一张图是未缩放的二维数据集，训练集用圆形表示，测试集用三角形表示。
第二张图使用相同的数据集，使用MinMaxScaler缩放，调用fit作用在训练集上，然后调用transform作用在测试集和训练集上，与第一张相比只是坐标轴刻度发生了变化，所有的特征都位于0和1之间，但是测试数据的特征的最大值和最小值并不是1和0。
第三张图对训练集和测试集分别进行缩放，此时对于训练集和测试集而言，特征的最大值和最小值都是1和0，但是测试集相对于训练集的移动不一致，因为它们分别做了不同的缩放。

# 更快捷高效的方法
# 所有具有 transform 方法的模型也都具有一个fit_transform 方法
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
# 依次调用fit和transform（使用方法链）
X_scaled = scaler.fit(X).transform(X)
# 结果相同，但计算更加高效
X_scaled_d = scaler.fit_transform(X)

虽然 fit_transform 不一定对所有模型都更加高效，但在尝试变换训练集时，使用这一方法仍然是很好的做法。

预处理对监督学习的作用

from sklearn.svm import SVC
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target,random_state=0)
svm = SVC(C=100)
svm.fit(X_train, y_train)
print("Test set accuracy: {:.2f}".format(svm.score(X_test, y_test)))

# 使用MinMaxScaler对数据进行缩放，然后在拟合SVC
# 使用0-1缩放进行预处理
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)

# 在缩放后的训练数据上学习SVM
svm.fit(X_train_scaled, y_train)
# 在缩放后的测试集上计算分数
print("Scaled test set accuracy: {:.2f}".format(svm.score(X_test_scaled, y_test)))

#可以通过改变使用的类将一种预处理算法轻松替换成另一种
# 因为所有的预处理类都具有相同的接口，都包含 fit 和 transform 方法
# 利用零均值和单位方差的缩放方法进行预处理
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
# 在缩放后的训练数据上学习SVM
svm.fit(X_train_scaled, y_train)
# 在缩放后的测试集上计算分数
print("SVM test accuracy: {:.2f}".format(svm.score(X_test_scaled, y_test)))

运行结果：
Test set accuracy: 0.94
Scaled test set accuracy: 0.97
SVM test accuracy: 0.96

数据缩放的作用非常显著。

降维、特征提取与流形学习

无监督学习进行数据变换最常见的目的就是可视化、压缩数据，以及寻找信息量更大的数据表示以用于进一步的处理。

主成分分析

PCA是一种旋转数据集的方法，旋转后的特征在统计上不相关。在做完这种旋转之后，通常是根据新特征对解释数据的重要性来选择它的一个子集。

mglearn.plots.plot_pca_illustration()

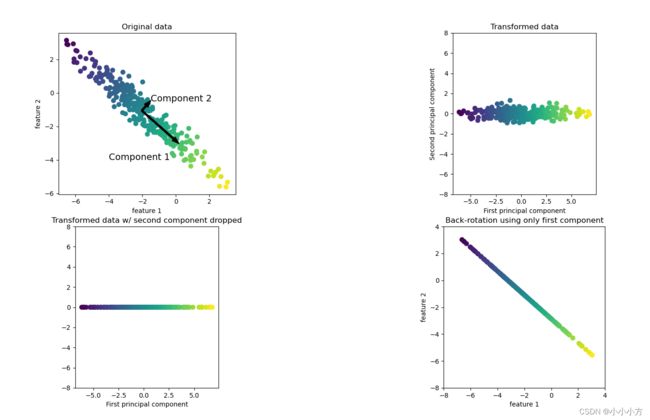
第一张图显示的是原始数据点，用不同颜色加以区分。算法首先找到方差最大的方向，标记为成分1，这是数据中包含最多信息的方向（向量），沿着这个方向的特征之间最为相关。然后，算法找到与第一个方向正交且包含最多信息的方向。在二维空间中，只有一个成为直角的方向，但是在高维的空间中会有很多的正交方向。这个过程中找到的方向被称为主成分，因为它们是数据方差的主要方向，一般来说，主成分的个数与原始特征相同。
第二张图显示的是同样的数据，但现在将其旋转，使得第一主成分与x轴平行且第二主成分与y轴平行。在旋转之前，从数据中减去平均值，使得变换后的数据以零为中心。在 PCA 找到的旋转表示中，两个坐标轴是不相关的，也就是说，对于这种数据表示，除了对角线，相关矩阵全部为零。
第三张图通过仅保留一部分主成分来使用PCA降维，仅保留第一个主成分。
第四张图没有保留原始特征之一，而是找到了最有趣的方向并保留这一方向，反向旋转并将平均值重新加回到数据中，这些数据点位于原始特征空间中，但我们仅仅保留了第一主成分中包含的信息，这种变换有时用于去除数据中的噪声影响，或者将主成分中保留的信息可视化。

将PCA应用于cancer数据集并可视化

PCA最常见的应用之一就是将高维数据集可视化。对于有两个以上特征的数据很难绘制散点图。对于乳腺癌数据集，具有30个特征的散点图，可以使用一种更简单的可视化的方法，对每个特征分别计算两个类别的直方图。

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()

fig, axes = plt.subplots(15, 2, figsize=(10, 20))
# 分别取出
malignant = cancer.data[cancer.target == 0]
benign = cancer.data[cancer.target == 1]
# 打散为一维数组
ax = axes.ravel()
for i in range(30):
    # 直方图分布
    _, bins = np.histogram(cancer.data[:, i], bins=50)
    ax[i].hist(malignant[:, i], bins=bins, color=mglearn.cm3(0), alpha=.5)
    ax[i].hist(benign[:, i], bins=bins, color=mglearn.cm3(2), alpha=.5)
    ax[i].set_title(cancer.feature_names[i])
    ax[i].set_yticks(())
ax[0].set_xlabel("Feature magnitude")
ax[0].set_ylabel("Frequency")
ax[0].legend(["malignant", "benign"], loc="best")
# 调整整体空白
fig.tight_layout()
plt.show()

为每个特征都创建了一个直方图，计算具有某一特征的数据点在特定范围内（bin）出现的频率.每张图都包含两个直方图，一个是良性类别的所有点（蓝色），一个是恶性类别的所有点（红色）。这样我们可以了解每个特征在两个类别中的分布情况，也可以猜测哪些特征能够更好地区分良性样本和恶性样本。
但是，这种图无法向我们展示变量之间的相互作用以及这种相互作用与类别之间的关系。利用 PCA，我们可以获取到主要的相互作用，并得到稍为完整的图像。我们可以找到前两个主成分，并在这个新的二维空间中用散点图将数据可视化.

# 在应用 PCA 之前，我们利用 StandardScaler 缩放数据，使每个特征的方差均为 1
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
scaler = StandardScaler()
scaler.fit(cancer.data)
X_scaled = scaler.transform(cancer.data)
'''
学习并应用 PCA 变换与应用预处理变换一样简单
我们将 PCA 对象实例化，调用 fit 方法找到主成分，
然后调用 transform 来旋转并降维。
默认情况下，PCA 仅旋转（并移动）数据，但保留所有的主成分。
'''
from sklearn.decomposition import PCA
# 保留数据的前两个主成分
pca = PCA(n_components=2)
# 对乳腺癌数据拟合PCA模型
pca.fit(X_scaled)
# 将数据变换到前两个主成分的方向上
X_pca = pca.transform(X_scaled)
print("Original shape: {}".format(str(X_scaled.shape)))
print("Reduced shape: {}".format(str(X_pca.shape)))

# 现在对两个主成分作图
# 对第一个和第二个主成分作图，按类别着色
plt.figure(figsize=(8, 8))
mglearn.discrete_scatter(X_pca[:, 0], X_pca[:, 1], cancer.target)
plt.legend(cancer.target_names, loc="best")
# 令xy的尺度相同
plt.gca().set_aspect("equal")
plt.xlabel("First principal component")
plt.ylabel("Second principal component")
plt.show()

运行结果：
Original shape: (569, 30)
Reduced shape: (569, 2)

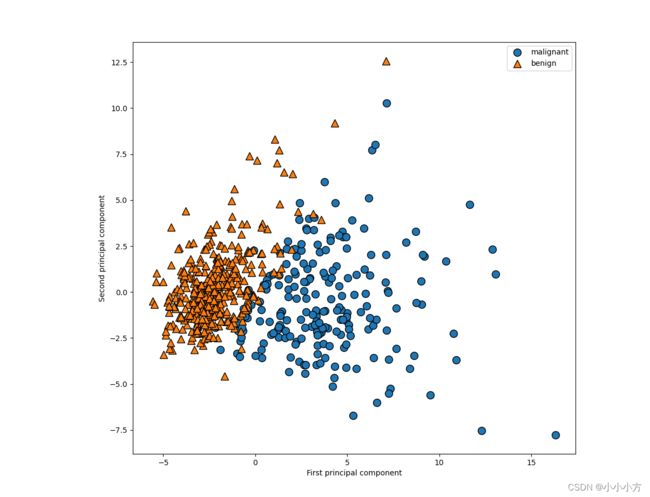
PCA是一种无监督方法，在旋转方向时没有用到任何类别信息。他只是观察数据中的相关性，散点图我们绘制了第一主成分和第二主成分的关系，然后利用类别信息对数据点进行着色，可以看出即使是使用线性分类器也可以在区分这两个类别时表现的不错，恶性点比良性点更加分散。
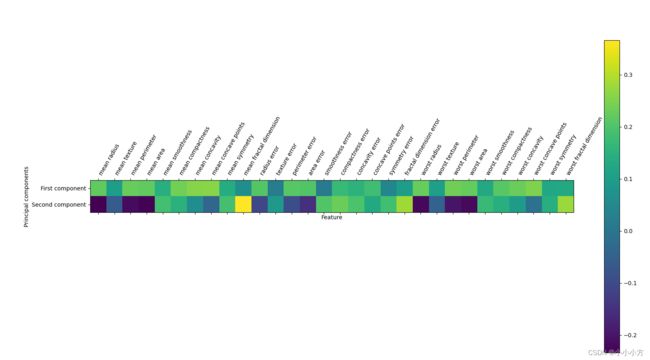
PCA 的一个缺点在于，通常不容易对图中的两个轴做出解释。主成分对应于原始数据中的方向，所以它们是原始特征的组合。但这些组合往往非常复杂。

# 拟合过程中，主成分被保存在PCA对象的components_属性中
print("PCA component shape: {}".format(pca.components_.shape))
print("PCA components:\n{}".format(pca.components_))
# 用热图将系数可视化
# 一个绘制矩阵的函数
plt.matshow(pca.components_, cmap='viridis')
plt.yticks([0, 1], ["First component", "Second component"])
plt.colorbar()
plt.xticks(range(len(cancer.feature_names)),cancer.feature_names, rotation=60, ha='left')
plt.xlabel("Feature")
plt.ylabel("Principal components")
plt.show()

运行结果：
CA component shape: (2, 30)
PCA components:
[[ 0.21890244  0.10372458  0.22753729  0.22099499  0.14258969  0.23928535
   0.25840048  0.26085376  0.13816696  0.06436335  0.20597878  0.01742803
   0.21132592  0.20286964  0.01453145  0.17039345  0.15358979  0.1834174
   0.04249842  0.10256832  0.22799663  0.10446933  0.23663968  0.22487053
   0.12795256  0.21009588  0.22876753  0.25088597  0.12290456  0.13178394]
 [-0.23385713 -0.05970609 -0.21518136 -0.23107671  0.18611302  0.15189161
   0.06016536 -0.0347675   0.19034877  0.36657547 -0.10555215  0.08997968
  -0.08945723 -0.15229263  0.20443045  0.2327159   0.19720728  0.13032156
   0.183848    0.28009203 -0.21986638 -0.0454673  -0.19987843 -0.21935186
   0.17230435  0.14359317  0.09796411 -0.00825724  0.14188335  0.27533947]]

特征提取的特征脸

PCA的另一个应用是特征提取，就是可以找到一种数据表示，比给定的原始表示更适合于分析。特征提取有一个很好用的实例就是图像。

# 特征提取
from sklearn.datasets import fetch_lfw_people
people = fetch_lfw_people(min_faces_per_person=20, resize=0.7)
image_shape = people.images[0].shape
fix, axes = plt.subplots(2, 5, figsize=(15, 8),
subplot_kw={'xticks': (), 'yticks': ()})
for target, image, ax in zip(people.target, people.images, axes.ravel()):
    ax.imshow(image)
    ax.set_title(people.target_names[target])
plt.show()

人脸识别的常见任务就是看某个未知的图像是否属于数据库中某个已知人物。最简单的方法是使用单一最近邻分类器，寻找与你要分类的人脸最为相似的人脸。

# 特征提取
from sklearn.datasets import fetch_lfw_people

people = fetch_lfw_people(min_faces_per_person=20, resize=0.7)
image_shape = people.images[0].shape
fix, axes = plt.subplots(2, 5, figsize=(15, 8),

subplot_kw={'xticks': (), 'yticks': ()})
for target, image, ax in zip(people.target, people.images, axes.ravel()):
    ax.imshow(image)
    ax.set_title(people.target_names[target])
plt.show()

print("people.images.shape: {}".format(people.images.shape))
print("Number of classes: {}".format(len(people.target_names)))

# 计算每个目标出现的次数
counts = np.bincount(people.target)
# 将次数与目标名称一起打印出来
for i, (count, name) in enumerate(zip(counts, people.target_names)):
    print("{0:25} {1:3}".format(name, count), end=' ')
    if (i + 1) % 3 == 0:
        print()
# 为了降低数据集的倾斜，对每个人只取50张图片
# np.zeros返回一个给定形状和类型用0进行填充的数组
mask = np.zeros(people.target.shape, dtype=np.bool)

for target in np.unique(people.target):
    # np.where()输出满足条件 (即非0) 元素的坐标
    mask[np.where(people.target == target)[0][:50]] = 1
X_people = people.data[mask]
y_people = people.target[mask]
# 将灰度值缩放到0到1之间，而不是在0到255之间以得到更好的数据稳定性
X_people = X_people / 255.

from sklearn.neighbors import KNeighborsClassifier
# 将数据分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_people, y_people, stratify=y_people, random_state=0)
# 使用一个邻居构建KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train, y_train)
print("\n")
print("Test set score of 1-nn: {:.2f}".format(knn.score(X_test, y_test)))

运行结果：
people.images.shape: (3023, 87, 65)
Number of classes: 62
Alejandro Toledo           39 Alvaro Uribe               35 Amelie Mauresmo            21 
Andre Agassi               36 Angelina Jolie             20 Ariel Sharon               77 
Arnold Schwarzenegger      42 Atal Bihari Vajpayee       24 Bill Clinton               29 
Carlos Menem               21 Colin Powell              236 David Beckham              31 
Donald Rumsfeld           121 George Robertson           22 George W Bush             530 
Gerhard Schroeder         109 Gloria Macapagal Arroyo    44 Gray Davis                 26 
Guillermo Coria            30 Hamid Karzai               22 Hans Blix                  39 
Hugo Chavez                71 Igor Ivanov                20 Jack Straw                 28 
Jacques Chirac             52 Jean Chretien              55 Jennifer Aniston           21 
Jennifer Capriati          42 Jennifer Lopez             21 Jeremy Greenstock          24 
Jiang Zemin                20 John Ashcroft              53 John Negroponte            31 
Jose Maria Aznar           23 Juan Carlos Ferrero        28 Junichiro Koizumi          60 
Kofi Annan                 32 Laura Bush                 41 Lindsay Davenport          22 
Lleyton Hewitt             41 Luiz Inacio Lula da Silva  48 Mahmoud Abbas              29 
Megawati Sukarnoputri      33 Michael Bloomberg          20 Naomi Watts                22 
Nestor Kirchner            37 Paul Bremer                20 Pete Sampras               22 
Recep Tayyip Erdogan       30 Ricardo Lagos              27 Roh Moo-hyun               32 
Rudolph Giuliani           26 Saddam Hussein             23 Serena Williams            52 
Silvio Berlusconi          33 Tiger Woods                23 Tom Daschle                25 
Tom Ridge                  33 Tony Blair                144 Vicente Fox                32 
Vladimir Putin             49 Winona Ryder               24 

Test set score of 1-nn: 0.23

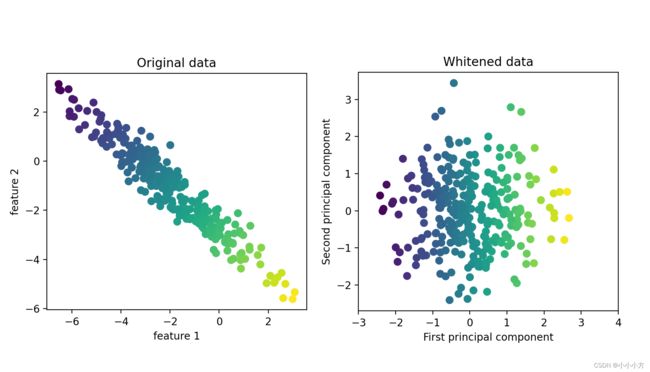
度量人脸的相似度，计算原始像素空间中的距离是一种糟糕的方法，用像素表示来比较两张图像时，我们比较的是每个像素的灰度值与另一张图像对应位置的像素的灰度值，使用这种原始表示很难获取到面部特征，使用言责主成分方向的距离可以提高精度。启用PCA的白化选项，它将主成分缩放到相同的尺度，变换后的结果与使用standarsscaler相同，白化不仅对应于旋转数据，还对应于缩放数据使其形状是圆形而不是椭圆。

mglearn.plots.plot_pca_whitening()

# 对训练数据拟合PCA对象，提取前100个主成分
pca = PCA(n_components=100, whiten=True, random_state=0).fit(X_train)
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
print("X_train_pca.shape: {}".format(X_train_pca.shape))

# 对新表示使用单一最近邻分类器对图像进行分类
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train_pca, y_train)
print("Test set accuracy: {:.2f}".format(knn.score(X_test_pca, y_test)))

# 对主成分进行可视化
print("pca.components_.shape: {}".format(pca.components_.shape))
fix, axes = plt.subplots(3, 5, figsize=(15, 12),subplot_kw={'xticks': (), 'yticks': ()})
for i, (component, ax) in enumerate(zip(pca.components_, axes.ravel())):
    ax.imshow(component.reshape(image_shape),cmap='viridis')
    ax.set_title("{}. component".format((i + 1)))
plt.show()

运行结果：
X_train_pca.shape: (1547, 100)
Test set accuracy: 0.31
pca.components_.shape: (100, 5655)

无法理解这些成分的所有内容，但是可以猜测一些主成分捕获到了人脸图像的哪些方面。虽然这种表示比原始像素值的语义稍
强，但它仍与人们感知人脸的方式相去甚远。由于 PCA 模型是基于像素的，因此人脸的相对位置（眼睛、下巴和鼻子的位置）和明暗程度都对两张图像在像素表示中的相似程度有很大影响。但人脸的相对位置和明暗程度可能并不是人们首先感知的内容。在要求人们评价人脸的相似度时，他们更可能会使用年龄、性别、面部表情和发型等属性，而这些属性很难从像素强度中推断出来。重要的是要记住，算法对数据（特别是视觉数据，比如人们非常熟悉的图像）的解释通常与人类的解释方式大不相同。

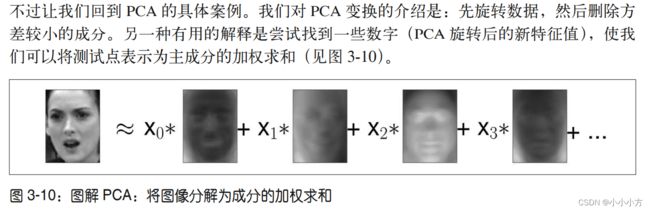
这里 x0、x1 等是这个数据点的主成分的系数，换句话说，它们是图像在旋转后的空间中的表示。我们还可以用另一种方法来理解 PCA 模型，就是仅使用一些成分对原始数据进行重建。
我们可以对人脸做类似的变换，将数据降维到只包含一些主成分，然后反向旋转回到原始空间。回到原始特征空间可以通过 inverse_transform 方法来实现。这里我们分别利用 10 个、50 个、
100 个和 500 个成分对一些人脸进行重建并将其可视化：

mglearn.plots.plot_pca_faces(X_train, X_test, image_shape)

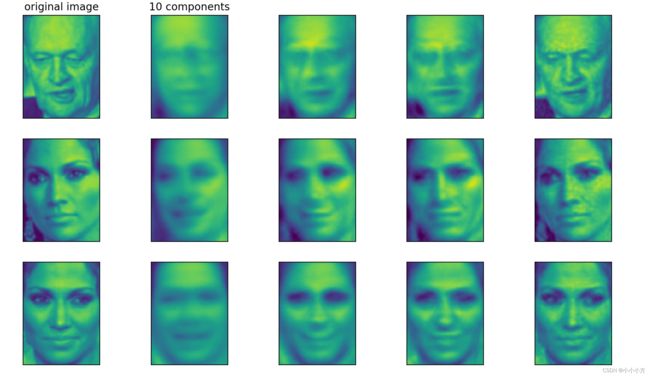
在仅使用前10个主成分时，捕获到了图片的基本特点，比如人脸的方向和明暗程度。随着使用的主成分越来越多，图像中也保留了越来越多的细节。如果使用的成分个数与像素的个数相等，意味着我们在旋转后不会丢失任何信息，可以玩么重建图像。
使用PCA的前两个主成分，将数据集中的所有人脸在散点图中可视化

mglearn.discrete_scatter(X_train_pca[:, 0], X_train_pca[:, 1], y_train)
plt.xlabel("First principal component")
plt.ylabel("Second principal component")
plt.show()

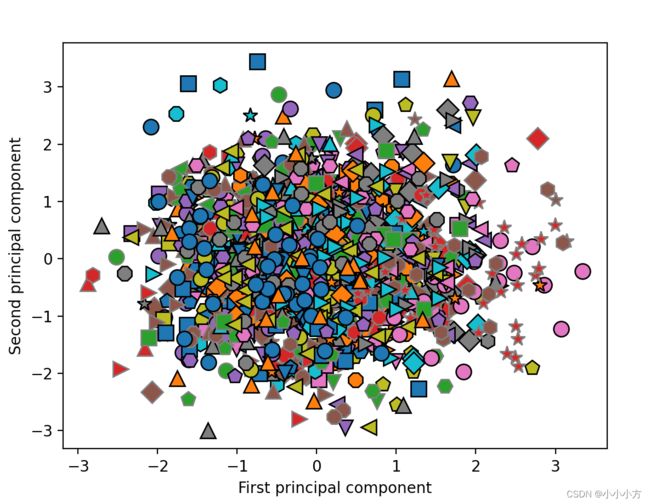
如上图所示，如果只使用两个主成分，整个数据就是一大团，看不到类别之间的分界。

非负矩阵分解

非负矩阵分解NMF是一种无监督学习算法，目的在于提取有用的特征。它的工作原理类似于PCA，也可以用于降维。与PCA相同，我们试图将每个数据点写成一些分量的加权求和。在PCA中，我们想要的是正交分量，并且能够解释尽可能多的数据方差，但是在NMF中，我们希望分量和系数均为非负，即分量和系数都大于或等于0。
将数据分解成飞赴加权求和的过程，对由多个独立源相加（叠加）创建而成的数据特别有用。NMF可以识别出组成合成数据的原始分量。

将NMF应用于模拟数据

首先需要保证数据是正的，数据相对原点（0，0）的位置对NMF非常重要，你可以将提取出来的非负分量看作是从（0，0）到数据的方向。

import mglearn
# 存在警告影响运行，忽略警告运行
import warnings
warnings.filterwarnings("ignore")
mglearn.plots.plot_nmf_illustration()

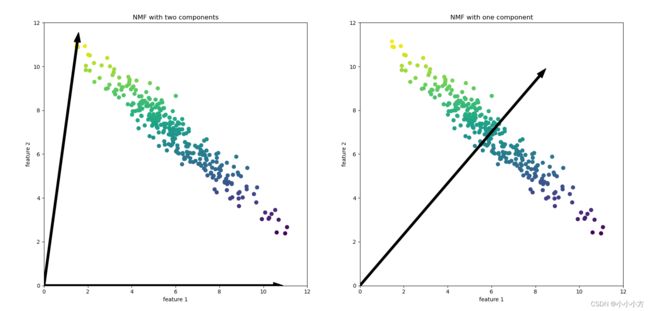
对于两个分量的NMF，所有数据点都可以写成这两个分量的正数组合。如果有足够多的分量能够完美的重建数据（分量个数与特征个数相等），算法会选择指向数据极值的方向。
如果我们只使一个分量，那么NMF会创建一个指向平均值的分量，因为指向这里可以对数据做出最好的解释。减少分量个数不仅会删除一些方向，而且会创建一组完全不同的分量！NMF的分量也没有按照任何特定方法排序，所有分量的地位平等。
NMF使用了随机初始化，根据随机种子的不同可能会产生不同的结果。

将NMF应用与人脸图像

NMF的主要参数是我们想要提取的分量的个数，通常来讲，这个数字要小于输入特征的个数。

mglearn.plots.plot_nmf_faces(X_train, X_test, image_shape)

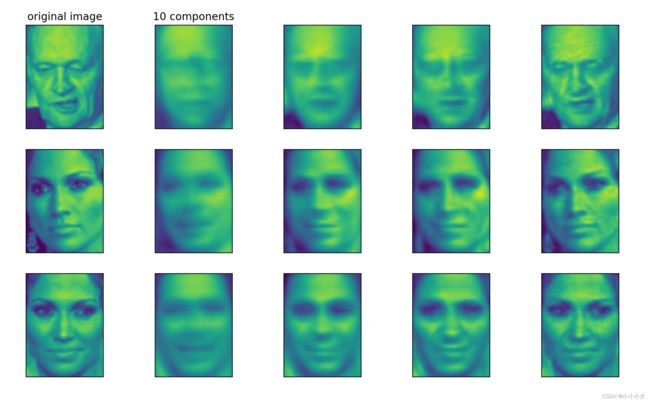
反向变换的数据质量与使用PCA时类似，但是要稍微差一些，因为PCA找到的是重建的最佳方向。NMF通常不用于对数据进行重建或编码，而是用于在数据中寻找有趣的模式。

# 提取一部分分量，初步观察一下数据
from sklearn.decomposition import NMF
nmf = NMF(n_components=15, random_state=0)

nmf.fit(X_train)
X_train_nmf = nmf.transform(X_train)
X_test_nmf = nmf.transform(X_test)

fix, axes = plt.subplots(3, 5, figsize=(15, 12),subplot_kw={'xticks': (), 'yticks': ()})
for i, (component, ax) in enumerate(zip(nmf.components_, axes.ravel())):
    ax.imshow(component.reshape(image_shape))
    ax.set_title("{}. component".format(i))
plt.show()

这些分量都是正的，可以清楚地看到，分量 3（component 3）显示了稍微向右转动的人脸，而分量 7（component 7）则显示了稍微向左转动的人脸。

compn = 3
# 按第3个分量排序，绘制前10张图像
# np.argsort 按大小进行排序，提取索引 [::-1]取从后向前的元素
inds = np.argsort(X_train_nmf[:, compn])[::-1]
fig, axes = plt.subplots(2, 5, figsize=(15, 8),subplot_kw={'xticks': (), 'yticks': ()})
for i, (ind, ax) in enumerate(zip(inds, axes.ravel())):
    ax.imshow(X_train[ind].reshape(image_shape))
plt.show()


compn = 7
# 按第7个分量排序，绘制前10张图像
inds = np.argsort(X_train_nmf[:, compn])[::-1]
fig, axes = plt.subplots(2, 5, figsize=(15, 8),subplot_kw={'xticks': (), 'yticks': ()})
for i, (ind, ax) in enumerate(zip(inds, axes.ravel())):
    ax.imshow(X_train[ind].reshape(image_shape))
plt.show()

分量3系数较大的人脸都是向右看的人脸，分量7系数较大的人脸都是向左看的。提取这样的模式最适合于具有叠加结构的数据，包括音频，基因表达，文本数据。

假设我们对一个信号感兴趣，它是由三个不同信号源合成的。

# 将数据混合成100维的状态
# 使用 np.random.RandomState() 获取随机数生成器
A = np.random.RandomState(0).uniform(size=(100, 3))
# 获得矩阵
X = np.dot(S, A.T)
print("Shape of measurements: {}".format(X.shape))

# 用NNF还原这三个信号
nmf = NMF(n_components=3, random_state=42)
S_ = nmf.fit_transform(X)
print("Recovered signal shape: {}".format(S_.shape))

# 应用PCA
pca = PCA(n_components=3)
H = pca.fit_transform(X)

models = [X, S, S_, H]
names = ['Observations (first three measurements)','True sources','NMF recovered signals','PCA recovered signals']
fig, axes = plt.subplots(4, figsize=(8, 4), gridspec_kw={'hspace': .5},subplot_kw={'xticks': (), 'yticks': ()})
for model, name, ax in zip(models, names, axes):
    ax.set_title(name)
    ax.plot(model[:, :3], '-')
plt.show()

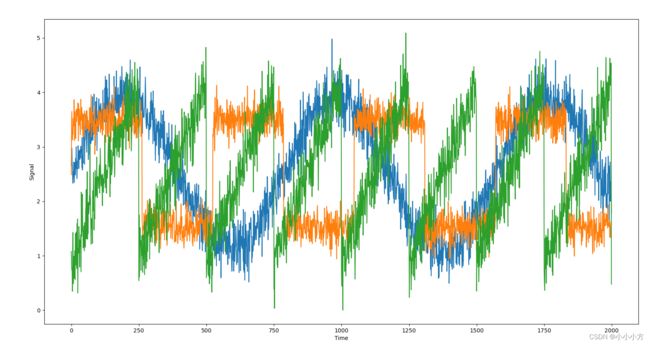
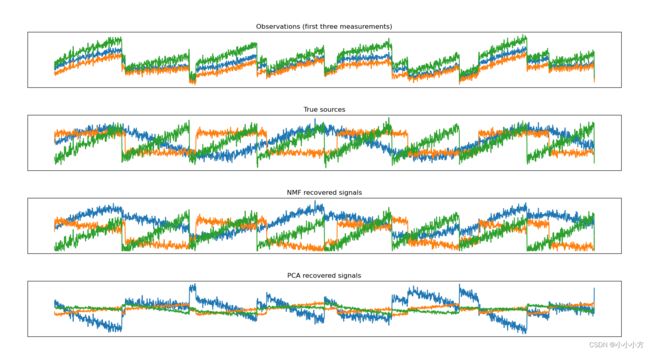
在这个例子中，我们无法观测到原始信号，只能观测到三个信号的混合叠加。我们想要将混合信号分解为原始分量，假设我们有许多种不同的方法来观测混合信号，每种方法都为我们提供了一系列的测量结果。上图中包含来自X的100次的测量中的3次，NMF在发现原始信号源时得到了不错的结果，而PCA仅使用第一个成分来解释数据中的大部分变化。虽然图中NMF分量的顺序与原始信号完全相同但是偶然，因为NMF生成的分量是没有顺序的。

用t-SNE进行流形学习

PCA通常是变换数据的首选方法，使得散点图可视化，但是这一方法需要先进行旋转再减少方向，限制了有效性。流形学习算法允许进行更复杂的映射，可以给出更好的可视化，最典型的是t-SNE算法。
流形学习算法主要用于可视化，很少用来生成两个以上的新特征。其中一些算法计算训练数据的一种新表示，但不允许变换新数据，这意味着这些算法不能用于测试集。t-SNE的思想是找到数据的一个二维表示，然后尝试让原始特征空间中距离较近的点更加靠近，原始特征空间中较远的点更加远离。t-SNE试图保存那些表示哪些带点比较靠近的信息。

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split

import mglearn

from sklearn.datasets import load_digits
digits = load_digits()
fig, axes = plt.subplots(2, 5, figsize=(10, 5),subplot_kw={'xticks':(), 'yticks': ()})
for ax, img in zip(axes.ravel(), digits.images):
    ax.imshow(img)
plt.show()

# 用PCA将降到二维的数据可视化，对前两个主成分作图，按照类别对数据点着色
# 构建一个PCA模型
pca = PCA(n_components=2)
pca.fit(digits.data)
# 将digits数据变换到前两个主成分的方向上
digits_pca = pca.transform(digits.data)
colors = ["#476A2A", "#7851B8", "#BD3430", "#4A2D4E", "#875525","#A83683", "#4E655E", "#853541", "#3A3120", "#535D8E"]
plt.figure(figsize=(10, 10))
plt.xlim(digits_pca[:, 0].min(), digits_pca[:, 0].max())
plt.ylim(digits_pca[:, 1].min(), digits_pca[:, 1].max())
for i in range(len(digits.data)):
    # 将数据实际绘制成文本，而不是散点
    plt.text(digits_pca[i, 0], digits_pca[i, 1], str(digits.target[i]),color = colors[digits.target[i]],fontdict={'weight': 'bold', 'size': 9})
plt.xlabel("First principal component")
plt.ylabel("Second principal component")
plt.show()

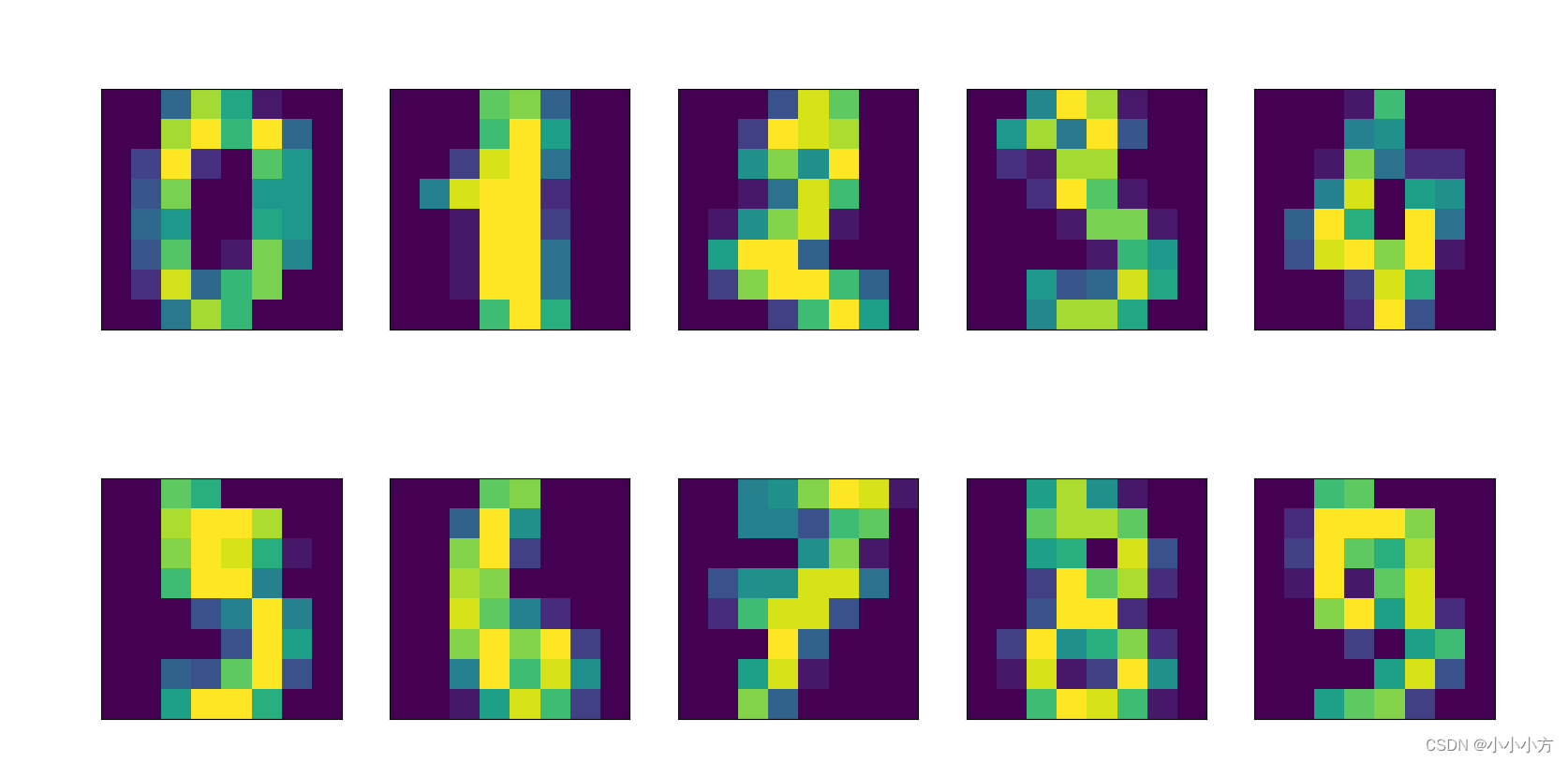
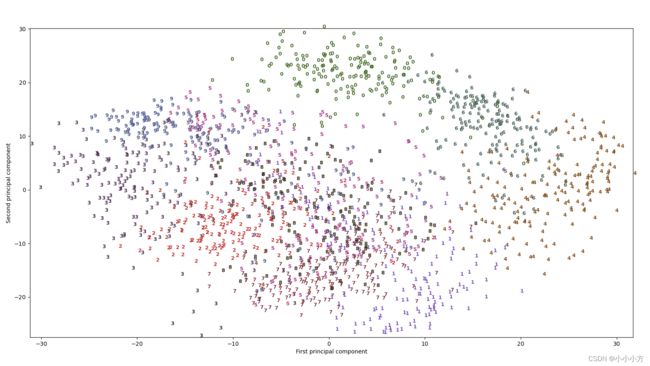
用每个类别的对应数字作为符号来显示每个类别的位置，利用前两个主成分可以将数字0，6，4较好的分开，但是其他大部分数字都大量的重叠在一起。我们将 t-SNE 应用于同一个数据集，并对结果进行比较。由于 t-SNE 不支持变换新数据，所以 TSNE 类没有 transform 方法。我们可以调用 fit_transform 方法来代替，它会构建模型并立刻返回变换后的数据。

#应用t-SNE
from sklearn.manifold import TSNE
tsne = TSNE(random_state=42)
# 使用fit_transform而不是fit，因为TSNE没有transform方法
digits_tsne = tsne.fit_transform(digits.data)
plt.figure(figsize=(10, 10))
plt.xlim(digits_tsne[:, 0].min(), digits_tsne[:, 0].max() + 1)
plt.ylim(digits_tsne[:, 1].min(), digits_tsne[:, 1].max() + 1)
for i in range(len(digits.data)):
    # 将数据实际绘制成文本，而不是散点
    plt.text(digits_tsne[i, 0], digits_tsne[i, 1], str(digits.target[i]),color = colors[digits.target[i]],fontdict={'weight': 'bold', 'size': 9})
plt.xlabel("t-SNE feature 0")
plt.xlabel("t-SNE feature 1")
plt.show()

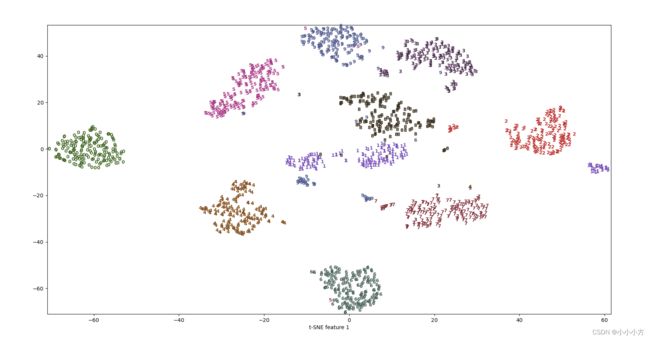
t-SNE 的结果非常棒。所有类别都被明确分开。数字 1 和 9 被分成几块，但大多数类别都形成一个密集的组。要记住，这种方法并不知道类别标签：它完全是无监督的。但它能够找到数据的一种二维表示，仅根据原始空间中数据点之间的靠近程度就能够将各个类别明确分开。t-SNE 算法有一些调节参数，虽然默认参数的效果通常就很好。你可以尝试修改perplexity 和 early_exaggeration，但作用一般很小。