Ekar : Explainable Knowledge Graph-based Recommendation via Deep Reinforcement Learning解析

Ekar : Explainable Knowledge Graph-based Recommendation via Deep Reinforcement Learning解析

---

提示：写完文章后，目录可以自动生成，如何生成可参考右边的帮助文档

---

一、前言

1. 本文的研究点：

• 解决知识图谱的可解释性较低的问题；
• 希望生成如图所示的一条路径，这条路径能够解释为什么推荐这个项目；
  
  在图片中，这条路径是用户–看过–>泰坦尼克号–主演–>小李子–主演–>罗密欧和朱丽叶。

2. 方法的关键点

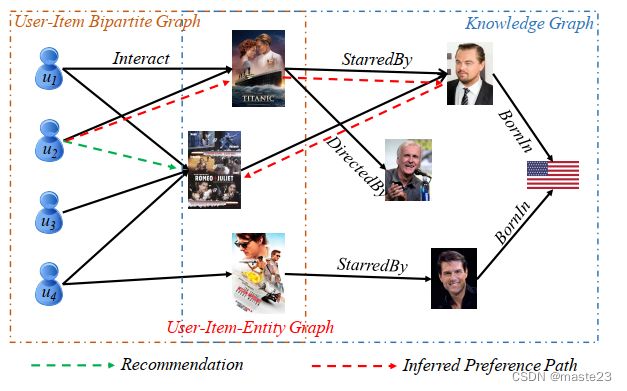
1. 推荐Agent从目标用户开始，通过依次选择用户-项目-实体图上的行走，将其路径扩展到相关项目。在训练过程中，如果起始用户和终端实体恰巧是推荐数据中存在的一次用户与项目之间的交互，我们就给这条路径分配一个正的奖励。
2. 考虑到由于巨大的探索空间，奖励在开始时可能是非常稀疏的，我们通过reward shaping[17]进一步增强奖励信号，其中软奖励函数首先使用最先进的知识图嵌入方法学习。
3. 我们使用REINFORCE[29]算法来最大化 我们的推荐代理的预期奖励。

二、方法介绍

这里的介绍是按照马尔科夫决策过程进行的。

1. 马尔科夫决策过程

States ： $s_t=(r_0,e_0,r_1,e_1,...r_t,e_t)\in {\mathcal{S}}_t$, $r_t\in {\mathcal{R}}^{\prime }$和$e_t\in {\mathcal{V}}^{\prime }$ 。初始化的状态$s_0=(r_0,e_0)$代表着开始的目标用户，$r_0$是人工引进的边。${\mathcal{R}}^{\prime }$ 是边的集合，其中包括知识图谱中的边和用户项目交互关系，${\mathcal{V}}^{\prime }$包括知识图谱中的实体和用户、项目节点。
Actions ：当实体处于状态$s_t$，动作是当前所处实体的出节点集合，具体而言，对于状态$s_t$而言，实体空间是${\mathcal{A}}_t=\{a=(r^{\prime },e^{\prime })|(e_t,r^{\prime },e^{\prime })\in {\mathcal{G}}^{\prime }\}$
Transition ： 如果下一步的行动被设定为$a_t=(r_{t+1},e_{t+1})$则下一步的状态$s_{t+1}=\{r_0,e_0,...r_t,e_t,r_{t+1},e_{t+1}\}$。
Rewards ： 给定终点状态$e_T$，$R_T=1$如果项目是用户交互过的项目，为0如果不是用户交互过的项目，为-1如果不是项目类别。

2.策略网络

基于LSTM对当前的状态进行编码：
$${\mathbf{s}}_0=LSTM(0,[{\mathbf{r}}_0;{\mathbf{e}}_0])$$
$${\mathbf{s}}_t=LSTM({\mathbf{s}}_{t-1},[{\mathbf{r}}_t;{\mathbf{e}}_t])$$
基于MLP预测每个项目的交互概率：
$${\mathbf{y}}_t={\mathbf{W}}_{2}ReLU({\mathbf{W}}_1{\mathbf{s}}_t+{\mathbf{b}}_1)+{\mathbf{b}}_2$$
采取行为$a^{\prime }$的概率是：
$$\pi (a^{\prime }|s_t)=softmax({\mathbf{a}}^{\prime }{\mathbf{y}}_t)$$

3. 奖励增强

$$R_T=\{\begin{array}{ll}1,& \text{ if }{e}_T\in \mathcal{I}\text{ and }<e_0,\bar{r},e_T>\in {\mathcal{G}}^{\prime },\\ \sigma \left(\psi \left(e_0,\bar{r},e_T\right)\right),& \text{ if }{e}_T\in \mathcal{I}\text{ and }<e_0,\bar{r},e_T>\notin {\mathcal{G}}^{\prime },\\ -1,& \text{ otherwise, }\end{array}$$
其中，$\sigma$是sigmoid激活函数，$\psi (e_0,\bar{r},e_T)=-||e_0+\bar{r}-e_T||$。

4. 网络优化

基于Reinforce方法进行优化：
$$J(\theta )={\mathbb{E}}_{e_0\in \mathcal{U}}\left[{\mathbb{E}}_{a_1,a_2,\dots ,a_T\sim {\pi }_{\theta }\left(a_t\mid s_t\right)}\left[R_T\right]\right];$$
$${\nabla }_{\theta }J(\theta )\approx {\nabla }_{\theta }\sum _t{R}_T\log {\pi }_{\theta }\left(a_t\mid s_t\right)$$