排序算法（线性时间排序）

说明：比较排序算法的复杂度下界是 O(nlog(n))

一、计数排序（复杂度是O(n)）

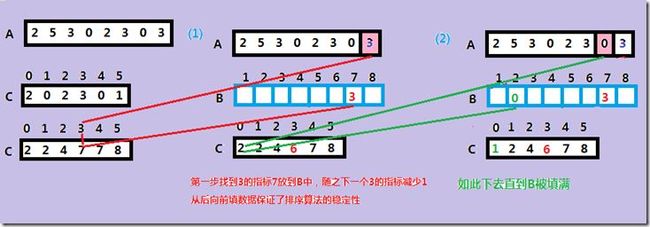
计数排序要求被排序元素都是整数型变量，即元素能用数组的指标表示

（1）统计个元素 i 的个数

（2）计算不超过 i 包括 i 的元素的个数

（3）将元素 i 放入适当的位子。

算法复杂度第一大步统计数字是n+k，其中k表示数字可能取到的最大的数

第二步需要复杂度是O(n),因此总的复杂度是 O(n+k). 当k=O(n)时，复杂度是O(n).

// counting_sort.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <vector>
#include <iostream>
using namespace std;
//此程序是实现计数排序算法，要特别注意指标问题
//2011/3/25 肖成
void counting_sort(vector<int> A, vector<int>& B, int k);
int main()
{
	int a[]={1,4,3,2,0,4,3,5,7,5,4,6,7,8,5,9,6,4,3,4,0};
	int k=9;
	vector<int> A(a,a+20);
	vector<int> B(20,0);
	counting_sort(A, B, k);
	vector<int>::iterator i;
	for(i=B.begin();i!=B.end();i++)
		cout<<*i<<"  ";
	return 0;
}

void counting_sort(vector<int> A, vector<int>& B, int k)
{
	vector<int> C(k+1,0);
	//统计A中重复元素的个数，C的指标表示这个元素的值，C的值表示对应元素的个数
	for(int j=0;j<A.size();j++)
		C[A[j]]=C[A[j]]+1;
	//统计这个值在数组中的放置的位置，即排在第几位
	for(int i=1;i<=k;i++)
		C[i]=C[i]+C[i-1];
	//一次将A中的每个元素放到正确的位置，计入数组下标应从0开始，因此用C[A[j]]减去1
	for(int j=A.size()-1;j>=0;j--)
	{
		B[C[A[j]]-1]=A[j];
		C[A[j]]=C[A[j]]-1;
	}
}

二、基数排序（是基于计数排序的算法）

对于比较大的一列整数，如329，457，736，823，67，384如果用计数排序就不能用了，因为k很大

这时可以使用基数排序，即按照位依次排，如下图所示

每一步用一次计数排序

假设数的位数是d，有n个数，则总的算法复杂度是 O(d(n+k)) 这里的k<9

复杂度关于 n 几乎是线性关系。

三、桶排序（期望时间复杂度O(n)）

桶排序算法想法类似于散列表

首先要假设待排序的元素输入符合某种均匀分布，例如数据均匀分布在[ 0,1）区间上.

则可将此区间划分为10个小区间，称为桶，每个桶存放一个链表，对散布到同一个桶

中的元素在排序。

// bucketsort.cpp : 定义控制台应用程序的入口点。
// 桶排序算法，要用到前面的堆排序算法进行桶内的排序
//肖成 2011/3/28
#include "vectorheap.h"
#include <iostream>
#include <list>
#include <algorithm>
#include <cstdlib>
using namespace std;

vector<vector<double>> bucket_sort(vector<double> vec);

int main()
{
	double a[]={0.34,0.21,0.41,0.11,0.32,0.42,0.22,0.51,0.62,0.71};

	vector<double> vec(a,a+10);
	vector<vector<double>> lstvec;

	lstvec=bucket_sort(vec);
	vector<double>::iterator vecIter;
	vector<vector<double>>::iterator lstIter;
	
	for(lstIter=lstvec.begin(); lstIter!=lstvec.end();lstIter++)
	{
		for(vecIter=(*lstIter).begin();vecIter!=(*lstIter).end();vecIter++)
			cout<<*vecIter<<"  ";
	}
	cout<<endl;
	return 0;
}

//从大到小排序
vector<vector<double>> bucket_sort(vector<double> vec)
{
	int n=vec.size();
	vector<vector<double>> lst(n);
	vector<vector<double>>::iterator iter;

	//计算散布到桶的位置，因为是从大到小所以要倒序散布
	for(int i=0;i<n;i++)
		lst.at((int)(n-n*vec.at(i))).push_back(vec.at(i));
	
	for(int i=n-1; i>=0; i--)
	{
		//对桶内的元素进行堆排序
		vectorheap<double> vecheap(lst.at(i));
		lst.at(i)=vecheap.sortHeap();
	}
	return lst;
}