数据分析之 —— 常用的统计学指标

数据分析是指用适当的统计分析方法对收集来的大量数据进行分析，将它们加以汇总和理解并消化，以求最大化地开发数据的功能，发挥数据的作用。数据分析是为了提取有用信息和形成结论而对数据加以详细研究和概括总结的过程。

要更好地进行数据分析，必须练好基本功，掌握常用的统计学指标。下面，让我们看看 Python 对统计计算的支持吧。

在 Python 标准库中，有专门的 数学统计函数 ，就在 statistics 模块里面。该模块提供了用于计算数字 (Real-valued) 数据的数理统计量的函数。

此模块并不是诸如 NumPy ， SciPy 等第三方库或者诸如 Minitab ， SAS ， Matlab 等针对专业统计学家的专有全功能统计软件包的竞品。此模块针对图形和科学计算器的水平。

要使用 statistics 模块，需要先进行导入：import statistics as stats 。

现在，开始吧！（ 非统计学相关专业，记得留意其方法名称， 例如算术平均数为什么是 mean 而不是 average 。譬如应用心理学专业也必须学习统计学知识。）

集中趋势

集中趋势又称“数据的中心位置”、“集中量数”等。它是一组数据的代表值。集中趋势的概念就是平均数的概念，它能够对总体的某一特征具有代表性，表明所研究的舆论现象在一定时间、空间条件下的共同性质和一般水平。就变量数列而言，由于整个变量数列是以平均数为中心而上下波动的，所以平均数反映了总体分布的集中趋势，它是表明总体分布的一个重要特征值。根据变量数列的平均数，就可以了解所研究总体的集中趋势和一般特征。集中趋势是用来描述舆论现象的重要统计分析指标，常用的有平均数、中位数和众数等，它们在不同类型的分布数列中有不同的测定方法。

算术平均数

样本平均值（mean），也称为样本算术平均值或简单的平均值，是数据集中所有项的算术平均值。它是数据的中心位置的度量。

l = [x + 1 for x in range(10)]

stats.mean(l)

中位数

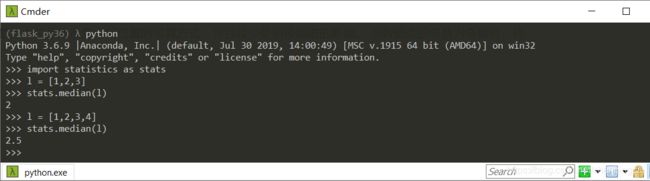
样本中位数是排序数据集的中间元素。中位数是衡量中间位置的可靠方式，并且较少受到极端值（异常值）的影响。 当数据点的总数为奇数时，将返回中间数据点：

l = [1,2,3]

median(l)
# 2

当数据点的总数为偶数时，中位数将通过对两个中间值求平均进行插值得出：

l = [1,2,3,4]

median(l)
# 2.5

众数

众数是指在统计分布上具有明显集中趋势点的数值，代表数据的一般水平。 也是一组数据中出现次数最多的数值。

l = [1, 1, 2, 3, 3, 3, 3, 4]

stats.mode(l)
# 3

---

以上，你知道什么情况下不能用算术平均吗？就是人们常常说的，“被平均”。

---

差异量数

差异量数亦称变异量数，又称离散趋势量数，它是统计学的基本概念之一，是表示样本数据偏离中间数值的趋势的量数，或者说它是反映样本频率分布离散程度的量数。

样本方差

样本方差用来表示一列数的变异程度。样本均值又叫样本均数。即为样本的均值。均值是指在一组数据中所有数据之和再除以数据的个数。

l = [2.75, 1.75, 1.25, 0.25, 0.5, 1.25, 3.5]

stats.variance(l)
# 1.3720238095238095

如果你已经计算过数据的平均值，你可以将其作为可选的第二个参数 xbar 传入以避免重复计算：

m = mean(data)
variance(data, m)

样本标准差

标准差表示的就是样本数据的离散程度。标准差就是样本平均数方差的开平方，标准差通常是相对于样本数据的平均值而定的，表示样本某个数据观察值相距平均值有多远。

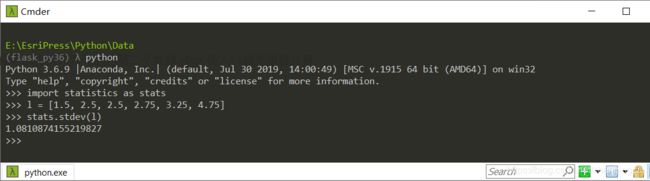
l = [1.5, 2.5, 2.5, 2.75, 3.25, 4.75]

stats.stdev(l)
# 1.0810874155219827