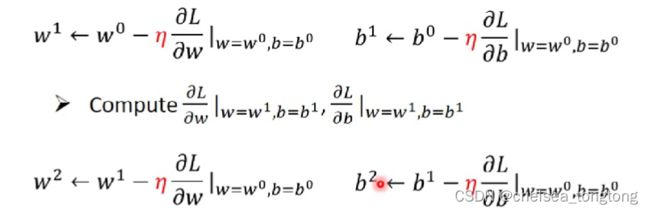深度学习课程笔记——回归、精灵宝可梦案例

目录

1 Regression Case

1.1 Current Case

1.1.1 Senario

1.1.2 Task

2 Regression Steps

2.1 Design A Model

2.2 Goodness Of Function 

2.2.1 Error Surface

2.3 Best Function

2.3.1 Gradient Descent

3  Model Selection

4 Redesign The Model

4.1 Back to step1:Redesign The Modle first

4.2  Back to step1:Redesign The Modle Again

4.3  Back to step2:Regularization

1 Regression Case

regression：回归问题
即找到一个函数 function，通过输入特征 x ，输出一个数值 Scalar

举例说明：
股市预测（Stock market forecast）
　　　　输入：过去10年股票的变动、新闻咨询、公司并购咨询等
　　　　输出：预测股市明天的平均值

自动驾驶（Self-driving Car）
　　　　输入：无人车上的各个sensor的数据，例如路况、测出的车距等
　　　　输出：方向盘的角度

商品推荐（Recommendation）
　　　　输入：商品A的特性，商品B的特性
　　　　输出：购买商品B的可能性

1.1 Current Case

1.1.1 Senario

首先根据已有的data来确定Senario，我们拥有宝可梦进化前后cp值的这样一笔数据，input是进化前的宝可梦(包括它的各种属性)，output是进化后的宝可梦的cp值；因此我们的data是labeled，使用的Senario是Supervised Learning（有监督学习）

1.1.2 Task

然后根据我们想要function的输出类型来确定Task，我们预期得到的是宝可梦进化后的cp值，是一个scalar(标量的)，因此使用的Task是Regression

2 Regression Steps

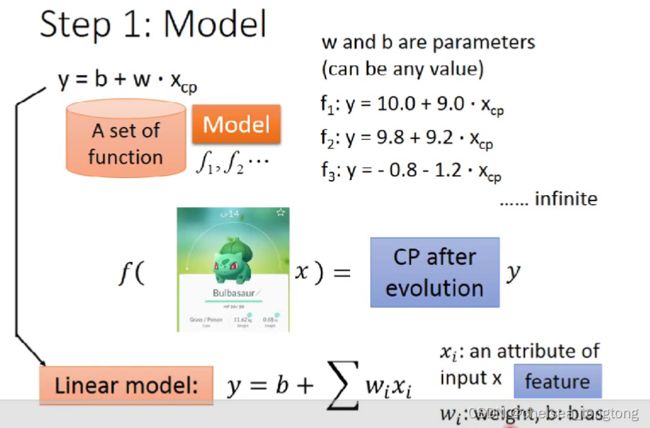
2.1 Design A Model

•  我们可以先建立一个最简单的线性函数来加深对模型的描述。
• 同一个model，不同参数有不同function。

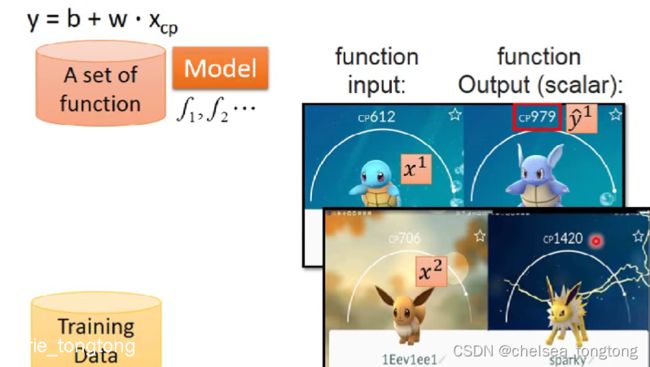
2.2 Goodness Of Function 

•  cp值代表一个宝可梦的武力值，yhat表示一个宝可梦进化后武力的真实值
• 在设计好一个模型后，我们输入cp值来产生模型生成的预测值
• 预测值和真实值还是有一定误差的，那么我们通过一个损失函数（loss function)来判定模型的好坏

• 我们可以通过真实值减去预测值然后再平方，因为10个宝可梦，所以10个平方求和，即所求的损失函数。这就是均方误差(MSE)
• 判断loss并不是只有这一种函数，在我们判断一个loss的时候，可以有很多种方式（目前见到的有e=y-y与e=（y-y）²这两种）
  即MAE和MSE

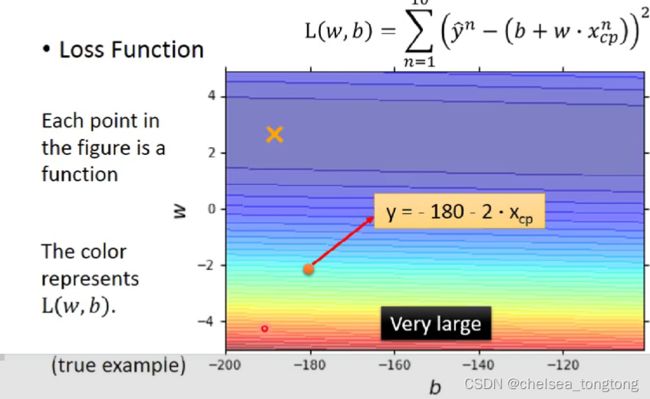
2.2.1 Error Surface

我们通过不同的parameter可以求出不同的loss，而根据loss做出的误差图就叫Error Surface。

•  图片上每一个点表示一个二维参数坐标，如（-180，12）表示b=-180,w=-2
• 颜色越深，比如红色表示损失函数越大，越不好

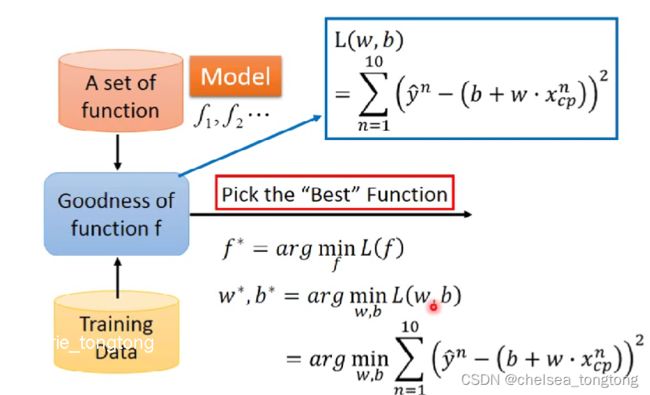
2.3 Best Function

•  线性代数方法可以解决找使得损失函数最小的参数
• 本文介绍的梯度下降法是optimization（最佳优化方法）

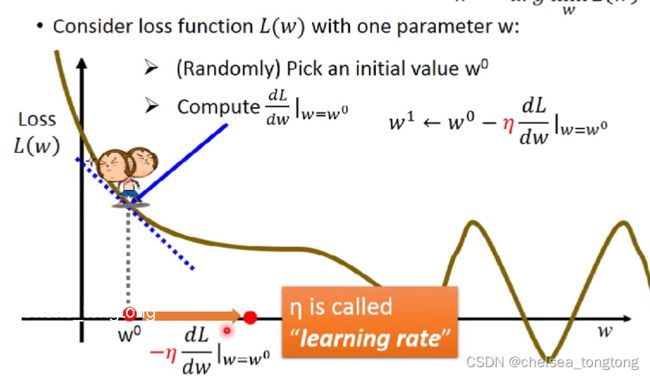
2.3.1 Gradient Descent

如图，如何使用gradient descent的方法来求一个w使得loss达到最小呢？

1、对于某一随机点，我们求其斜率，即,w这个参数对loss的微分
理由：我们可以通过切线的斜率来判断其走势，即是在变大还是在变小，这样就可以进行“移动”。

例如：上图切线斜率是负的，在切点左边是大的，切点右边是小的，我们目标是想要让损失函数变小，所一要往右边移动。但是切线斜率是正 的时候切点左边小，所以要往左边移动。
2、我们需要确定一个learning rate，来确定移动的距离。它取决于当前点的斜率，即斜率大时步伐可以大一点，斜率小时可以小一点。用η来表示。
其中learning rate 是自己设置的一个参数，用来调整学习速率
我们不难看出，gradient descent求得的w很有可能是一个local minima，这是个会产生的问题（但是是个假问题 ）

• local minima：局部最小（类比数学中的极值）
• Hyperparameters（超参数）

以上是对一个参数的例子，不难看出，多个参数时进行的步骤是近似的，仍需要各个参数分别来对loss微分。这样就能得出最终的结果。

3  Model Selection

  我们最终能否准确的得到正确的结果，减小其误差。
  最终取决的还是你对这个模块涉及的内容的理解程度，即Domain Knowledge。
而这样的简单模型很难做到一些稍微复杂的情况，所以它也有他的model bias，即某些情况是你永远无法“模仿”出来的。

• 线性模型 Linear models
• model bias：模型的限制（缺陷）
• threshold：阈值
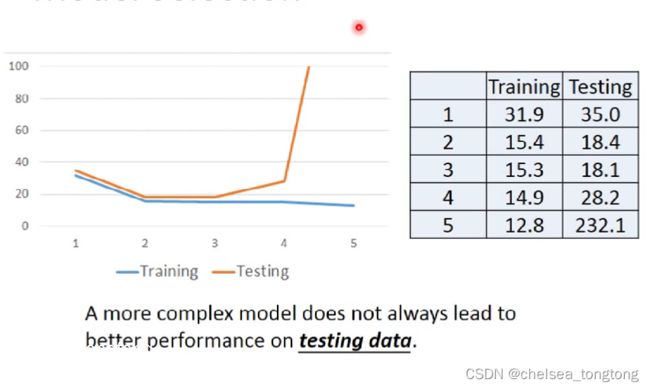
• Therefore,我们把model搞得越来越复杂，看看他的training error 和testing error 
• 从下表看出，我们可以选2，3次，但是3次武力值算出来不太符合实际，所以选择二次

• 虽然说training error 越复杂越小，但是testing error 不一定，可能会变大
• This is overfitting(过拟合）

4 Redesign The Model

4.1 Back to step1:Redesign The Modle first

当输入的精灵宝可梦越来越多，原来的模型不够灵活。不同的物种代入到不同的linear function进行预测。当输入Pigdey时，b1和w1的系数是1，其他b和w的参数是0

•  这也可以看成是linear function，b和w是回归系数，条件函数是x(feayure)\

4.2  Back to step1:Redesign The Modle Again

 我们把之前用loss function得出的最优的二次的function+function里面加上条件选择，得出以上的线性回归函数,模型太复杂了！过拟合了！

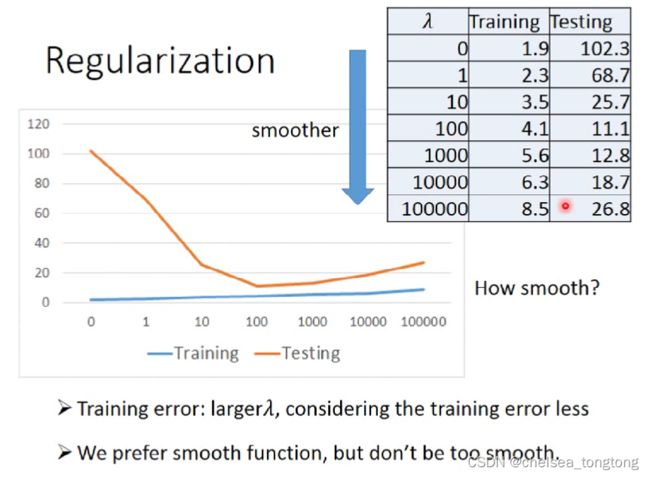
4.3  Back to step2:Regularization

regularization解决overfitting(L2正则化解决过拟合问题)

regularization可以使曲线变得更加smooth，training data上的error变大，但是 testing data上的error变小。

 原来的loss function只考虑了prediction的error，即 ；而regularization则是在原来的loss function的基础上加上了一项 ，就是把这个model里面所有的 的平方和用λ加权(其中i代表遍历n个training data，j代表遍历model的每一项)

 Q:为啥我们要让参数w更小，趋近于0，也就是更平滑？

因为参数值接近0的function，是比较平滑的；所谓的平滑的意思是，当今天的输入有变化的时候，output对输入的变化是比较不敏感的

举例来说，如果 越小越接近0的话，输出对输入就越不sensitive敏感，我们的function就是一个越平滑的function；说到这里你会发现，我们之前没有把bias——b这个参数考虑进去的原因是bias的大小跟function的平滑程度是没有关系的，bias值的大小只是把function上下移动而已

如何选择 λ，这个需要手动调优。

瞅，上图 training error是越来越大，testing error是越来越少再变大，当λ=100时，这是个转折点，于是我们选择他。