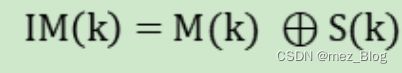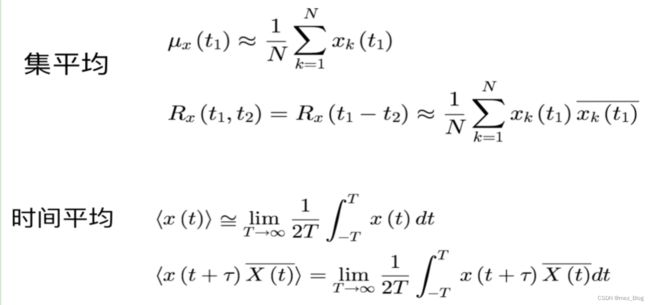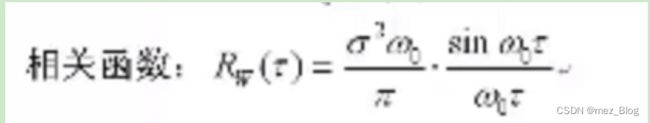系统辨识课程笔记
第一次课
- 现代控制理论有哪些部分组成
辨识、状态估计、控制理论
- 辨识方法主要采用什么技术
数理统计的技术
- 系统辨识的定义
系统辨识是根据系统的输入/输出时间函数,确定系统行为的数学模型,是现代控制理论的一个分支。
- 辨识模型具有(近似)性、(唯一)性,辨识方法亦有(多样)性。
- 辨识采用的测量数据的特点是什么
有噪声,有随机性
- 辨识方法的分类
经典辨识方法(非参数辨识):
阶跃相应辨识方法、脉冲相应辨识方法、频率相应辨识方法、相关分析辨识方法、谱分析辨识方法。
现代辨识方法(参数辨识):
最小二乘类辨识方法、梯度校正辨识方法、概率逼近辨识方法
- 通俗的说,系统辨识是研究什么的
是研究怎样利用对位置系统的实验数据或在线运行数据输入输出数据,建立描述系统的数学模型的科学,钱学森把系统广义概括为“依一定顺序相互联系着一组事物”。
- 现代辨识方法有哪些?
最小二乘类辨识方法、梯度校正辨识方法、概率逼近辨识方法、极大似然估计法
第二次课
- 什么是模型
模型把关于实际过程的本质的部分信息简缩成有用的描述形式。它是用来描述过程的运动规律,是过程的一种客观写照或缩影,是分析、预报、控制过程行为的有力工具,模型是实体的一种简化描述。模型保持实体的一部分特征,而将其它特征忽略或者变化,不同的简化方法得到不同的模型。
- 辨识所研究的模型有哪些形式
①“直觉”模型:(司机驾驶、地图、建筑模型)
②物理模型:实际过程的缩小(风洞模型、水力学模型、传热学模型、电力系统动态模型等)
③图表模型:以图表形式表现过程的特征(阶跃响应、脉冲响应、频率响应等)
④数学模型:以数学结构的形式反映过程的行为特征(代数方程、微分方程、差分方程、状态方程等参数模型)
- 模型的分类
①线性与非线性:系统线性和关于参数空间线性、本质和非本质线性。
②动态与静态
③确定性与随机性
④宏观与微观
- 本门课程研究的模型是什么样的?
线性的,随机的
- 建模的方法
·机理法:“白箱”理论
·测试法:“黑箱”理论(辨识)
·两者结合:“灰箱”理论
- 建模的基本原则
目的性、实在性、可辨识性、节省性
- 辨识的三要素
输入输出数据、模型类、等价准则
第三次课
- 辨识问题的常用表达形式是什么
最小二乘法
- 什么性质的系统可以描述为最小二乘格式
线性系统
- 什么是新息
不同时刻产生的新的信息
K时刻的实际输出与与过程输出预报值的差
- 求取输入误差的条件的前提条件是什么
模型可逆的,也就是说总可以找到一个产生给定输出的唯一输入
- 辨识的内容和步骤
辨识的主要内容:1.实验设计2.模型结构辨识3.模型参数辨识4.模型检验
辨识就是从观测到的含有噪声的输入输出数据中提取出数学模型的方法。根据现场情况,辨识分为在线辨识和离线辨识两种。
- 实验设计主要包括哪些内容
输入信号选择(幅度,频带等)、采样时间、辨识时间(数据长度)、开环或闭环辨识、离线或在线辨识
- 输入信号一般选择什么信号
持续激励的信号,常用的M序列
一般选用具有持续激励性、宽频性、优良性的信号,如M序列
- 采样时间的选择
- 满足采样定理,(2)与模型最终应用的采样时间保持一致
(3)采样时间不能太长或太短,经验公式:T0=T95/(5~15); T0采样时间;T95过程阶跃响应达到95%的调节时间
- 采样得到的输入输出能不能直接用?应该怎么做
不能,要进行零均值化和提出高频成分的预处理
- 怎样进行模型检验
利用等价准则进行模型检验
通过检验模型与过程输出残差序列的白色性,来判断模型的好坏
- 辨识技术的主要应用
- 用于控制系统的设计和分析;
(2)用于过程的在线控制;
(3)用于特定问题的预报、预测;
(4)用于监视过程参数并实现故障诊断:
- 辨识技术当今的发展热点
*非线性系统辩识(机器人) *快时变与有缺陷样本的辩识; *生命、生态系统的辩识;
*辩识的专家系统与智能化软件包的开发; *基于模糊理论、神经网络、小波变换的辩识方法;。
*系统辩识与人工智能、人工生命、图象处理、网络技术和多媒体技术的结合;
第n次课
- M序列又叫做什么?
最长线性移位寄存器序列
- 如何将(0,1)序列转换成(a,-a)序列
M(i)= a(1-2xi)
- M序列的定义
- 如何选择M序列的反馈通道?
反馈函数f(a1,a2,a3,…an)为非线性函数
- 什么叫做游程
M序列中某种状态连续出现的段称为“游程”
- 周期为2^P的M序列中取0的个数和取1的个数分别是多少?
0的次数为(2^P -1)/2 ; 1的次数为(2^P +1)/2
- 如何生成逆M序列?
设M(k)为周期为NP取值为0和1的M序列,S(k)为周期为2 的取值为0和1的方波序列,令
- 从提高辨识精度角度说,逆M序列优于M序列的原因?
逆M序列比M序列周期增加了一倍,逆M序列无直流分量,统计性质与白噪声类似,它是一种比M序列更为理想的伪随机码序列,在辨识领域中有更为广泛的应用。
逆M序列的谱密度类似于M序列,但是谱线疏一倍,且无直流成分,当选用逆M序列做辨识输入信号时,谱密度的这些特点有助于选择序列的参数,以获得更好的结果。
第五次课 (宽平稳(二阶))
- 系统辨识这门课程研究的信号平稳性是什么样的?
宽平稳(二阶)二维统计特性随着时间的推移,不发生变化
- 什么是集平均和时间平均 (课件上有)
- 什么是各态历经(各态遍历)
一条样本可以提取随机信号的各个特性。
各态历经就是随机过程中的任一次实现都经历了随机过程的所有可能状态。
![]()
- 什么是不相关(课件有)
互协方差函数等于0,即Cxy(τ)=0,
- 相关函数当时间常数无穷大时,相关函数的值为多少?
当随机信号不为周期信号时,时间常数无穷大,相关函数的值趋近为0
- 随机信号研究功率谱密度,如何求功率谱密度?
- 白噪声的功率谱密度是什么?
白噪声信号在各个频段上的功率是一样的,由于白光是由各种频率(颜色)的单色光混合而成,因而此信号的这种具有平坦功率谱的性质被称作是“白色的”,各频率分量在信号中的权值相同。白噪声功率谱密度在整个频域内均匀分布的噪声,即其功率谱密度为常数。
第六次课
- 白噪声的用途有哪些
- 进行仿真,来验证辨识方法是否有效
- 根据表现定理,输入白噪声,输出可以是自己想要的有色噪声
- 输入信号的好坏,影响中输出的精度。白噪声满足辨识的需要
- 伪随机数为什么不是严格的随机数
计算机产生的白噪声是一个近似的白噪声,而不是真正的白噪声。用数学方法产生的随机数,严格意思上来说不是一个白噪声。所以说,伪随机数不是严格的随机数。
伪随机数是有一个周期的,周期要求足够的长。
- 白噪声的相关函数是什么函数
- n维白噪声应该满足什么条件
- 如何应用白噪声生成有色噪声?
- 生成随机数有几种方法?
三类方法:Rand百万随机数、物理方法、数学方法
- 数学上生成随机数的方法分别是什么?
(0,1)均匀分布和正态分布随机数
- 怎样将(0-1)分布的随机数序列转换成正态分布的随机数序列?
- 统计近似抽样法:
设是(0,1)均匀随机数序列,则有:
由中心极限定理有
若
即有
由此可得正态分布的随机数
- 变样抽样法
设1和2相互独立的(0,1)均匀分布随机变量,则
是相互独立、服从N(0,1)分布的随机变量
第七次课
- 描述系统的方法有几种,分别是什么
两种,一种是非参数辨识,另一种是参数辨识。
- 辨识的方法分为几类,分别是什么
分为两类,分别是
经典辨识方法(非参数辨识):
阶跃相应辨识方法、脉冲相应辨识方法、频率相应辨识方法、相关分析辨识方法、谱分析辨识方法。
现代辨识方法(参数辨识):
最小二乘类辨识方法、梯度校正辨识方法、概率逼近辨识方法
- 如果用面积法求解传递函数,如何判别系统的阶次。
选择传递函数阶次的原则:判别各面积是否大于零。