2021李宏毅机器学习笔记--13 Network Compression
2021李宏毅机器学习笔记--13 Network Compression
- 摘要
- 一、Network Pruning(修剪)
-
- 1.1基本思想
- 1.2 why pruning
- 1.3 大乐透假设(Lottery Ticket Hypothesis)
- 1.4 Rethinking the Value of Network Pruning
- 1.5 Practical Issue
- 二、Knowledge Distillation(知识蒸馏)
-
- 2.1 Student and Teacher
- 2.2 Ensemble(合奏)
- 2.3 Temperature
- 三、Parameter Quantization(参数量化)
-
- 3.1 less bits
- 3.2 weight clustering
- 3.3 Binary Weights
- 四、Architecture Design(架构设计)
-
- 4.1 Low rank approximation(低秩近似)
- 4.2 Depthwise Separable Convolution(深度可分离卷积)
- 五、Dynamic Computation
-
- 5.1 Train multiple classifiers(训练大量的分类器(从小到大))
- 5.2 Classifiers at the intermedia layer(使用中间层输出)
- 总结
摘要
未来有可能将深度学习技术应用于一些移动设备上,但是这些设备有可能存储空间或者资源受到限制,不能存放过深或者过大的模型,也或者受限于计算能力,network不能有太多层或者太多参数。所以说network compression这件事非常重要,本篇文章着重介绍一些让network变小的方式。
一、Network Pruning(修剪)
1.1基本思想
神经网络的参数很多,但其中有些参数对最终的输出结果贡献不大而显得冗余,将这些冗余的参数剪掉的技术称为剪枝。剪枝可以减小模型大小、提升运行速度,同时还可以防止过拟合。
剪枝分为one-shot和iteration剪枝:
one-shot剪枝过程:训练模型–> 评估神经元(或者kernel、layer)的重要性–>去掉最不重要的神经元–> fine-tuning–>停止剪枝。
iteration剪枝过程:训练模型–> 评估神经元(或者kernel、layer)的重要性–>去掉最不重要的神经元–> fine-tuning–>判断是不是要继续剪枝,如果是回到第二步(评估神经元的重要性),否则停止剪枝。
1.2 why pruning
为什么要进行修剪?为什么不直接在数据集上训练小的模型,而是先训练大模型?有两个解释:
一是:因为模型越大,越容易在数据集上找到一个局部最优解,而小模型比较难训练,有时甚至无法收敛。
二是:大乐透假设(Lottery Ticket Hypothesis)
1.3 大乐透假设(Lottery Ticket Hypothesis)
提出大乐透假设试图解释为什么需要修剪。
我们先对一个network进行初始化(红色的weight),再得到训练好的network(紫色的weight),再进行pruned,得到一个pruned network
如果我们使用pruned network的结构,再进行随机初始化random init(绿色的weight),会发现这个network不能train下去
如果我们使用pruned network的结构,再使用原始随机初始化original random init(红色的weight),会发现network可以得到很好的结果。
所以有结论:可能神经元会不会被训练起来与初始值有很大关系,是一种大乐透现象。

1.4 Rethinking the Value of Network Pruning
作者通过数个网络和数据集的prune 测试,得到了三个观察和结论:
1.如果有一个确定的“压缩”模型,训练一个大网络不是必要的;
2.在prune算法中,我们所认为“重要”的权重,其实对裁剪的小模型来说,并不是那么有用;
3.对于最终的压缩小模型来说,通过prune算法得到的网络架构,比通过prune得到的“重要”的权重更加重要。
并得出一个最终结论:对于SOT的剪枝算法而言,使用裁剪的权重来fine-tune只能得到类似的或者更差的效果;对于通过剪枝算法得到的特定网络模型,可以直接随机初始化训练,而不用经历传统的裁剪管道(训练大网络,裁剪出权重,finetune小网络)。
同时,作者对彩票假说(Lottery Tickety Hypothesis)进行了对比,发现使用所谓最佳学习率的“中奖彩票”初始化,并未必随机初始化有更好的结果。
传统的prune算法有三个通道:
(1)训练一个大模型;
(2)按某指标来裁剪一个训练好的大模型;
(3)finetune裁剪模型以获得因prune而损失的性能;
在传统的prune观念中,有两个“通识”:
(1)训练大模型是必要的,可以从大模型中无损裁剪。一系列工作认为从大模型变小模型,要比直接训练一个小模型要好;
(2)裁剪下来的权重和网络架构都是重要的。所以,裁剪算法大都会选择fine-tune而不是重头训练它。
本文提出,对于结构化裁剪,上述观点都不重要。对于统一裁剪(使用百分比,在每个layer上都裁剪百分比的channal数)的小网络,也是随机初始化重头训练效果来得好;对于使用Prune算法自动获得模型结构的小网络,仍需一个较大网络,最后随机初始化训练比较好。
但对于非结构化裁剪(权重系数化等),从头训练并不能达到较好的效果。

1.5 Practical Issue
如果我们现在进行weight pruning,进行weight pruning之后的network会变得不规则,有些neural有2个weight,有些neural有4个weight,这样的network是不好implement(实行)出来的;
GPU对矩阵运算进行加速,但现在我们的weight是不规则的,并不能使用GPU加速;
实做的方法是将pruning的weight写成0,仍然在做矩阵运算,仍然可以使用GPU进行加速;但这样也会带来一个新的问题,我们并没有将这些weight给pruning掉,只是将它写成0了而已。
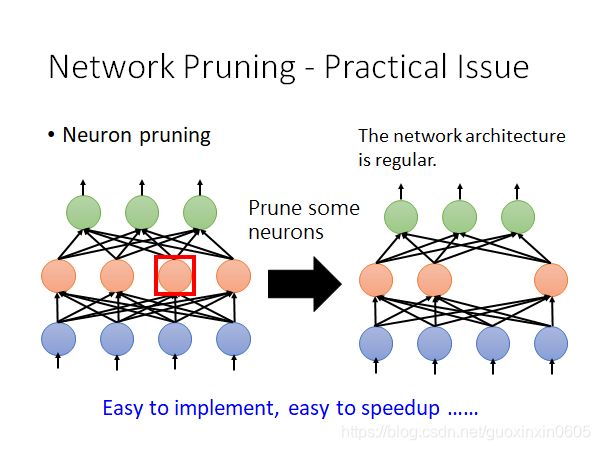
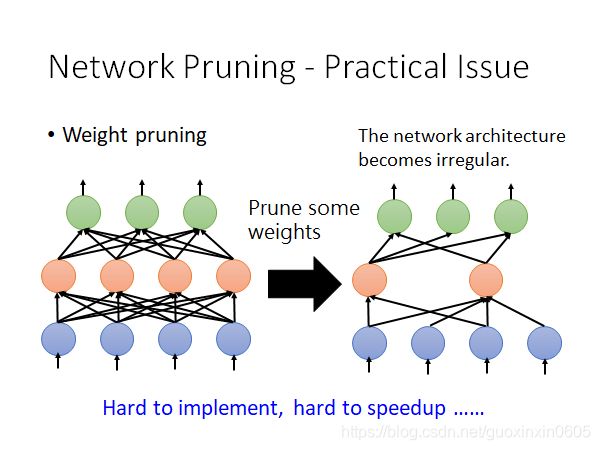 实际上做weight pruning是很麻烦的,通常我们都进行neuron pruning,可以更好地进行implement,也很容易进行speedup。
实际上做weight pruning是很麻烦的,通常我们都进行neuron pruning,可以更好地进行implement,也很容易进行speedup。
二、Knowledge Distillation(知识蒸馏)
2.1 Student and Teacher
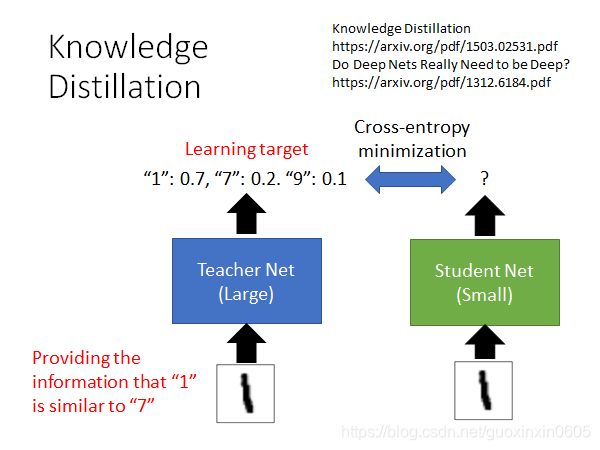
训练一个大网络,用小网络(Student Net)学习大网络。并计算两者之间的cross-entropy,使其最小化,从而可以使两者的输出分布相近。
teacher提供了比label data更丰富的资料,比如teacher net不仅给出了输入图片和1很像的结果,还说明了1和7长得很像,1和9长得很像;所以,student跟着teacher net学习,是可以得到更多的information的。
为什么这样有用?因为小网络学的是一个基于大网络的 distillation 。不仅仅学到一个输出神经元的价值,而是多个神经元的输出.
2.2 Ensemble(合奏)
在实际生活中,设备往往放不下太多的model,这时我们就可以使用Knowledge Distillation的思想,使用student net来对teacher进行学习,在实际的应用中,我们只需要student net的model就好.

2.3 Temperature
如图所示左边算式,三个不同的输入输出的三个预测值有两个是近似的,我们进行改进,加入参数T,令其为100,再次输入三个初始值。得到的预测值是完全可以区分的。
三、Parameter Quantization(参数量化)
3.1 less bits
一个很直观的方法就是使用更少bit来存储数值,例如一般默认是32位,那我们可以用16或者8位来存数据.
3.2 weight clustering
如下图所示,最左边表示网络中正常权重矩阵,之后我们对这个权重参数做聚类,比如最后得到了4个聚类,那么为了表示这4个聚类我们只需要2个bit,即用00,01,10,11来表示不同聚类。之后每个聚类的值就用均值来表示。这样的一个缺点就是误差可能会比较大。
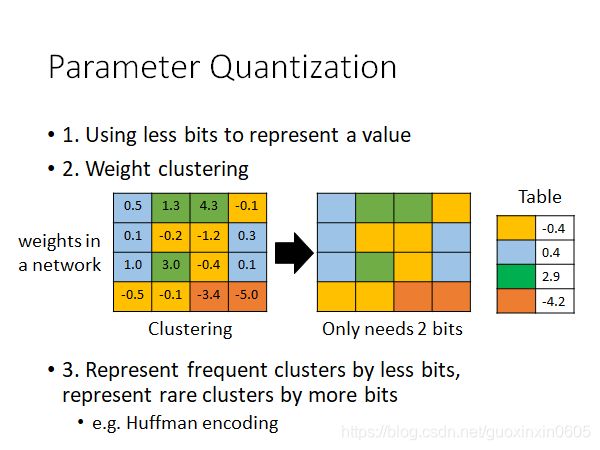
如图,只要保存各个参数的类别,以及类别对应的数值表就可以。
此外,还可以进行哈夫曼编码等压缩。
3.3 Binary Weights
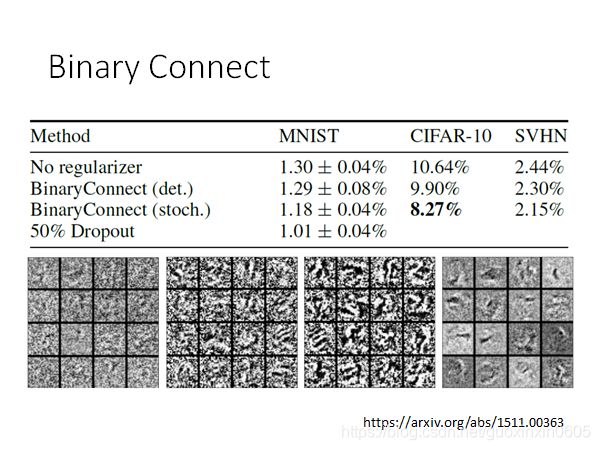
Binary Weights是以一种更加极致的思路来对模型进行压缩,即每个节点只有1或-1来表示,则参数就可以用一个位来表示了。
如下图示,灰色节点表示使用binary weight的神经元,蓝色节点可以是随机初始化的参数,也可以是真实的权重参数。
第一步我们先计算出和蓝色节点最接近的二元节点,并计算出其梯度方向(红色剪头)。
第二步,蓝色节点的更新方向则是按照红色箭头方向更新,而不是按照他自身的梯度方向更新。如下图示,梯度下降后,蓝色节点到了一个新的位置。
最后在满足一定条件后(例如训练之最大epoch),用离得最近的Binary Weight作为结果
 结果还不错,可以看到把权重限制为+1或者-1相当于加上了正则化。
结果还不错,可以看到把权重限制为+1或者-1相当于加上了正则化。
四、Architecture Design(架构设计)
4.1 Low rank approximation(低秩近似)
下图是低秩近似的简单示意图,左边是一个普通的全连接层,可以看到权重矩阵大小为M×NM×N,而低秩近似的原理就是在两个全连接层之间再插入一层K。是不是很反直观?插入一层后,参数还能变少?
没错,的确变少了,我们可以看看新插入一层后的参数数量为: N × K + K × M = K × ( M + N ) N×K+K×M=K×(M+N) N×K+K×M=K×(M+N),因为 K < M , K < N K 如图,标准的CNN架构,其中两个通道,4个filter,一共有72个参数。 首先是输入数据的每个通道只由一个二维的卷积核负责,即卷积核通道数固定为1,而不是像上面那样,每个卷积核的通道数和输入通道数保持一致。这样最后得到的输出特征图的通道数等于输入通道数。 因为第一步得到的输出特征图是用不同卷积核计算得到的,所以不同通道之间是独立的,因此我们还需要对不同通道之间进行关联。为了实现关联,在第二步中使用了 1 ∗ 1 1 * 1 1∗1大小的卷积核,通道数量等于输入数据的通道数量。另外 1 ∗ 1 1*1 1∗1卷积核的数量等于预期输出特征图的通道数,在这里等于4。最后我们可以得到和标准卷积一样的效果,而且参数数量更少:3∗3∗2+(1∗1∗2)∗4=26。 该方法的主要思路是如果目前的资源充足(比如你的手机电量充足),那么算法就尽量做到最好,比如训练更久,或者训练更多模型等;反之,如果当前资源不够(如电量只剩10%),那么就先算出一个过得去的结果。 比如说我们提前训练多种网络,比如大网络,中等网络和小网络,那么我们就可以根据资源情况来选择不同的网络。但是这样的缺点是我们需要保存多个模型,这在移动设备上的可操作性不高。 这样的思路其实也挺直观的,就是比如说我们做分类任务,当资源有限时,我们可能只是基于前面几层提取到的特征做分类预测,但是一般而言这样得到的结果会打折扣,因为前面提取到的特征是比较细腻度的,可能只是一些纹理,而不是比较高层次抽象的特征。 未来有可能将很多东西存储在移动设备上,但是对于具有更多层和节点的更大的神经网络,减少其存储和计算成本变得至关重要,特别是对于一些实时应用,如在线学习、增量学习以及自动驾驶。另一方面如何让深度模型在移动设备上运行,也是模型压缩加速的一大重要目标。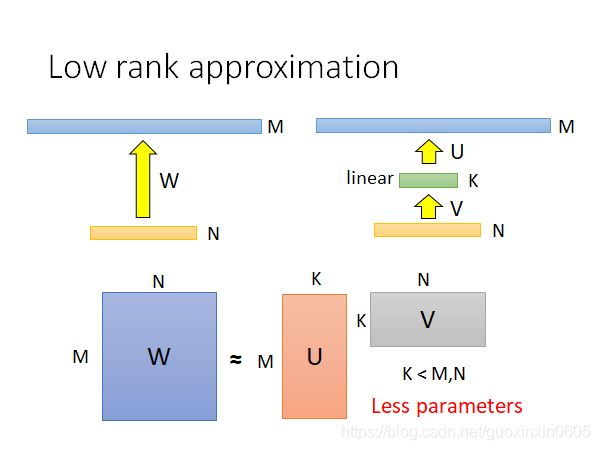 但是低秩近似之所以叫低秩,是因为原来的矩阵的秩最大可能是min(M,N),而新增一层后可以看到矩阵 U和 V 的秩都是小于等于 K的,我们知道rank(AB)≤min(rank(A),rank(B)), 所以相乘之后的矩阵的秩一定还是小于等于 K。那么这样会带来什么影响呢?那就是原先全连接层能表示更大的空间,而现在只能表示小一些的空间了。
但是低秩近似之所以叫低秩,是因为原来的矩阵的秩最大可能是min(M,N),而新增一层后可以看到矩阵 U和 V 的秩都是小于等于 K的,我们知道rank(AB)≤min(rank(A),rank(B)), 所以相乘之后的矩阵的秩一定还是小于等于 K。那么这样会带来什么影响呢?那就是原先全连接层能表示更大的空间,而现在只能表示小一些的空间了。4.2 Depthwise Separable Convolution(深度可分离卷积)

而Depthwise Separable卷积分成了两步,如下图示。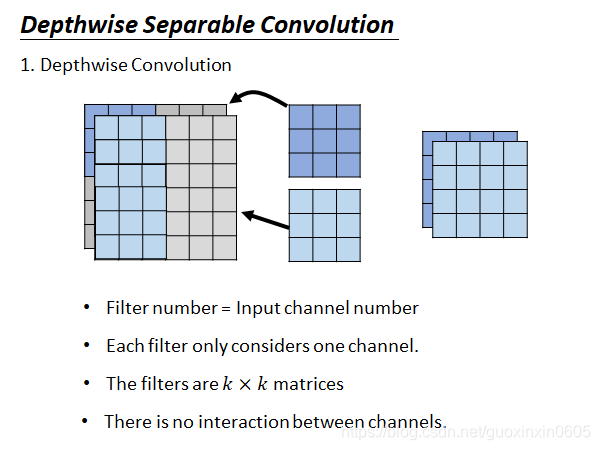
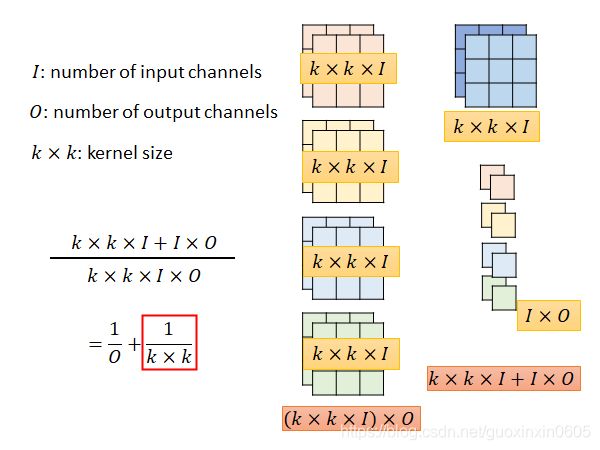
下面我们算一下标准卷积和Depthwise Separable卷积参数数量大小关系:假设输入特征图通道数为II,输出特征图通道数为O,卷积核大小为k×k。
标准卷积参数数量= k × k × I × O
Depthwise Separable卷积参数数量= k × k × I + I × O
因为通常输出特征图的通道数O会设置的比较大,所以可以看到Depthwise Separable卷积的参数量会明显少于标准卷积。
五、Dynamic Computation

5.1 Train multiple classifiers(训练大量的分类器(从小到大))
5.2 Classifiers at the intermedia layer(使用中间层输出)
总结


