算法设计与分析代码实现笔记
文章目录
- dynamic programming
-
- 矩阵链式乘法
-
- ==错误==使用递归实现动态规划的例子
- 使用迭代实现动态规划
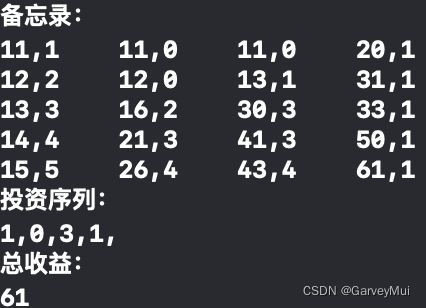
- 投资问题
- 背包问题
dynamic programming
矩阵链式乘法
确定结合律使用顺序以达到最小乘法次数
错误使用递归实现动态规划的例子
复杂度 O ( 2 n ) O(2^n) O(2n),由递推方程通过数学归纳法可证
#include 使用迭代实现动态规划
建立备忘录 O ( n 3 ) O(n^3) O(n3),通过标记函数获得最终括弧添加位置 O ( n ) O(n) O(n)
#include
#include 在源代码文件夹打开终端,使用
g++ -std=c++17 main.cpp -o main.out,生成可执行文件
sudo ./main.out,输入本机密码后,可执行文件获得sh执行权限,sh启动自动化脚本生成pdf文件。
pdf文件中矩阵运算次序指示:
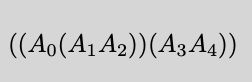
投资问题
时间复杂度上限 O ( n × m 2 ) O(n \times m^2) O(n×m2)
三层遍历处,最外层对列遍历有 n − 1 n-1 n−1次循环,内层等差数列求和,有 ( 1 + m ) m 2 \frac{(1+m)m}{2} 2(1+m)m次比较,乘法原理计数,共计 ( n − 1 ) ( 1 + m ) m 2 ≤ c ( n × m 2 ) , c \frac{(n-1)(1+m)m}{2} \le c(n \times m^2),c 2(n−1)(1+m)m≤c(n×m2),c为某一常数
#include 背包问题
#include
#include