聚类分析之系统聚类的R实现

1.系统聚类简介
系统聚类法是一种常用的聚类方法，假设有n个样品，每个样品有p个变量，系统聚类的基本步骤为：先将每个个体（样品或变量）各自看成一类，总共有r类（如果时Q型聚类，则r=n;如果时R型聚类，则r=p),根据个体间的相似程度（距离、相关系数等）将r类个体中最相似的一类合并称一类，得到r-1类，再在这r-1类中找出最相似的两类合并，得到r-2类，依次进行下去。
对于Q性聚类情形，设Gs与Gt为两个类，用dij表示Gs中第i个样品与Gt中第j个样品的距离，常用的度量Gs与Gt的距离Dst的方法有以下几种。
（1）最小距离法：Gs和Gt之间的距离Dst定义为两类最近样品之间的距离，即：

(2)最大距离法：Gs和Gt之间的距离Dst定义为两类最远样品之间的距离，即：

(3)中间距离法：Gs与Gt之间的距离取两者之间的距离，这是最大距离与最小距离的一种折中，其递推公式为：

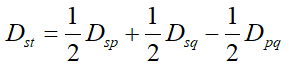
（4）重心距离法：Gs与Gt之间的距离定义为两类重心的距离，即：

（5）类平均距离法：Gs和Gt之间的距离Dst定义为两类元素两两之间距离的平均，即：

（6）离差平方和法：基于方差分析思想构建的分类方法，如果分类正确，同样样品的离差平方和应该较小，类与类的离差平方和应该较大。设Gt={Gp,Gq},则Gs与Gt之间的距离Dst的递推公式为：

对于R型聚类，设Gs和Gt为两个类，用rij表示Gs中第i个样品与Gt中第j个样品的的相似系数，通常用系数

作为Gs和Gt之间的相似系数。
2.举例说明：
用红酒的颜色，香味，酸度，甜度，纯度，果味数据对十类红酒进行分类。

a=read.table("C:/Users/MrDavid/data_TS/red_wine.csv",sep=",",header=T)
a
colnames(a)=c("wine","x1","x2","x3","x4","x5","x6")
a
d=dist(a,method="euclidean",diag=T,upper=F,p=2)
HC=hclust(d,method="single")
plot(HC)
#dist函数使用方法：
#dist(a,method为距离计算方法，包括"euclidean"(欧式距离),"manhattan"(绝对值距离)，
#"maximum"(切氏距离)，"minkowski"明氏距离"等，diag是是否包括对角元素，upper是否需要上三角元素)
#hclust函数的用法
#method为系统聚类法，包括"single"（最小距离法），"complete"(最大距离法)，“average"(类平均法)，
#"median"(中间距离法)，"centroid"(重心法)，"ward"(离差平方和法)

分类结果如下：

在此例中，我们使用的是欧式距离，最小距离法进行计算的。