新冠疫情预测
2020年2月春节前后, 新冠状病毒疫情打乱了所有中国人对春节假期的安排和对新年的向往, 我也是。本来是计划去东北的大城市走一趟的。 一家人都闷在家里一个月,没人知道疫情何时结束,什么时候能从新开始工作,开始上学和正常的生活,所有人都 很焦虑不安。于是向用一个有效的传染病疫情模型预测一下。
1. SIR模型简介
新冠状病毒疫情同2003年的非典疫情类似, 基本上从人群划分来看, 有如下特点:
- 健康人没有免疫力因此可能会被感染病毒,可称之为易感者
- 感染者具有传染性,因此可以传染给健康人将其变成感染者。
- 感染者或者死亡从而将被活化掩埋处理,或者治愈从而获得免疫力。总之死亡者和治愈者不再可能会感染病毒, 可称之为疫情移除者 。
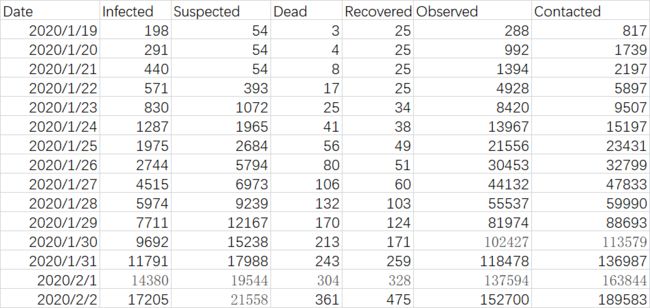
可用SIR (Suspectible,Infective and Removed )这三个字母来代表以上的三个人群: 易感者,感染者,疫情移除者。SIR 模型的目的就是对三类人群数量的变化建立数学模型,以此来预测疫情何时到达拐点 (感染者每日净增量由递增变为递减),峰值(累计感染者达到最大值或每天的感染者增量为零)和结束(累计感染者全部转化为移除者,净值为0)。对照卫健委每天发布的官方数据,如下所示, 包括确诊(Infected), 疑似(Suspected), Dead(死亡), Recovered(治愈),Observed (医学观察),Contacted (密切接触), SIR 的源数据如下:
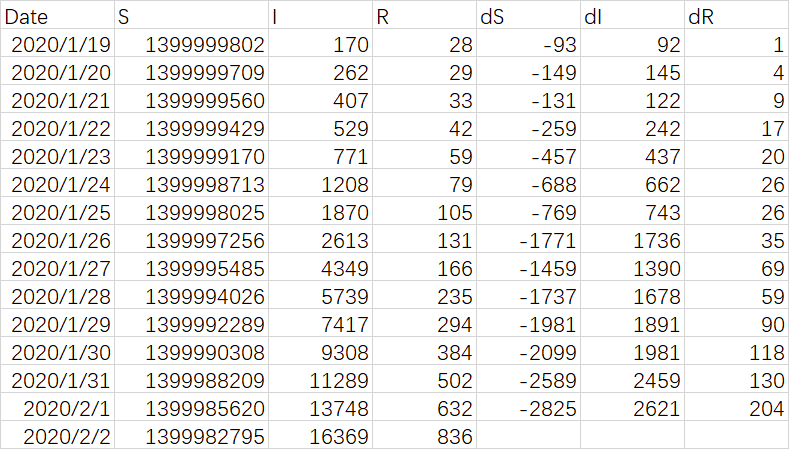
- Removed (移除者)是累计死亡和治愈之和:Dead + Recovered
- Infective(感染者) 是累计确诊数减去移除者数 : Infected - Removed
- Suceptible (易感者): 所有的除感染者和移除者之外的中国人都属于易感人群 :人口总量 N(14亿)- Removed - Infective
- Susceptible(S) + Infective (I) + Removed (R) = N
SIR 模型假设:
- 人口总数(N)保持不变,N 由 S易感者人数(S),感染者人数(I) 和移除者人数(R) 组成,N = S + I + R
- 易感者(S)与感染者(l)有效接触后,每天按一定的比率从易感者成为新的感染者。这个比率称为日接触率λ (读lambda) .
- 感染者经过治疗后每天按照一定的比率μ(读miu)从感染者成为移除者(R康复或死亡), 这个比率称作日治愈率或日移除率。
- 移除者(R)不会再次感染病毒或传染病毒给别人。
- 感染者(I)每天的增量是易感者(S)每天转化成I 与 每天I 转化成R的净值。
注意以上描述都是在围观描述S,I,R每天的增量或减量,在数学上可以用你微分方程来表示,如下所示:
dS/dt = -λ ·S/N · I (1)
dI/dt= λ ·S/N · I - μ·I (2)
dR/dt = μ ·I (3)
N = S + I + R (4)
虽然数学语言高度抽象,但以上方程和5点假设描述的是同样的意思。比如卫健委的数据是以天为单位发布的, 所以dt = 1(天)是每天的意思。
dR/dt 表示移除者R每天的增减:比如移除者2月1日相对于1月31日的增量,这个增量与当天的I成正比,比率为日治愈率μ.
dS/dt, 表示易感者每天的增量,它是一个负数,数值与当前易感者在总人口占比和当前感染者比正比,比率为日接触率λ 。
dI/dr , 表示感染者每天的净增量, 他是dS/dt的绝对值 和 dR/dt 差
S, I , R 各自的数值每天都不一样,但三者之和为人口总数N。N是常数。
此处最好有个图来描述,让这个变化过程形象起来,读者自己想象吧。
S,I,R都是关于t的未知的连续函数,如果能求出他们各自的解析解(S,I, R 的各自函数形式),然后将他们的图形画出来,那么未来趋势就一目了然了吧啊,不幸的是解析解无法求出,所幸的是我们的目的是预测未来一年的趋势,数值解同样能达到目的。
数值解是通过给定初值T0时S0,I0,R0,并利用微分方程组的微分等式,递归的计算未来(比如2020年1月到12月)每一天的St,It,Rt .
那么接下来的问题是确定微分方程组的参数 λ和μ了。
2. 常数接触率和治愈率的模型实现
SIR模型假设接触率λ和治愈率μ是常数的 , 每天S, I, R 的数值和他们的微分的可计算如下 .
R = 累计治愈+ 累计死亡, I = 累计确诊 - R, S = N - I - R.
dR/dt = Rt+1 - Rt, dI/dt = It+1 - It , dS/dt = St+1 - St .
然后将S, I, R, dR , dI 带入公式(2)和(3) , 利用最小二乘的优化方法可求出最优的常数接触率λ和治愈率μ . 然后在求出未来一年的常微分方程组(ODE)的数值解,再将这些数值在日期轴上画出来,就能开到未来了.下面是部分的matlab代码, 具体详见github .
sir_run.m
load('weijianwei'); %load the source data u = regress(dR(1:end-1), I(1:end-1) ); % optimize u lamda = regress(dI(1:end-1)+ dR(1:end-1), S(1:end-1).*I(1:end-1)/N); % optimize lamda %lamda=0.492112631178384; %optimized by using 1stopt %u=0.421005009555275; %optimized by using 1stopt %numeric solution of SIR ODE [t,y]=ode45('sir', [0,400], [1399999802 170 28]); % plot the the full SIR graph
...
sir.m : sir ODE
%S' = -lamda * S * I / N , susceptible
%I' = lamda * S * I /N - u * I , infetive , in hospitable
%R = u * I , recovered or dead , not in hospital
%S +I + R = N
function y=sir(t,x)
global lamda u N
y=[-lamda*x(1)*x(2)/N,lamda*x(1)*x(2)/N-u*x(2), u*x(2)]';
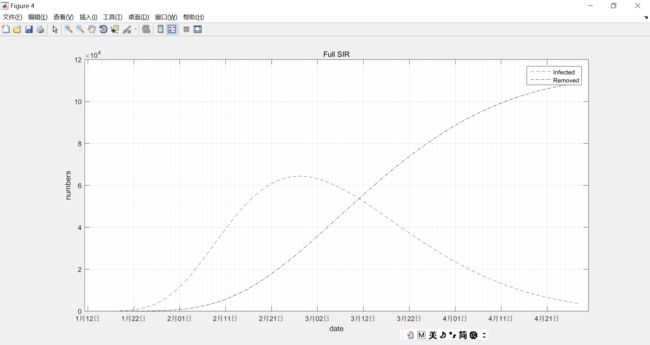
运行一下看看效果
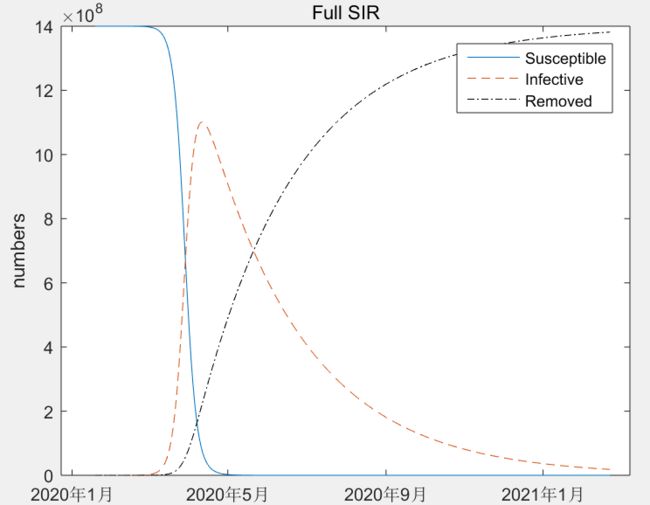
优化的效果很不理想, 14亿人口在5月前全部感染,高峰期感染11亿, ----- 这个不可能的 .....
看一下具体的日接触率λ和日治愈率μ 是多少呢, 如下
日接触率远大于治愈率,大概是24倍 , 这样的比率会造成易感者迅速大量感染,由于易感人群趋于零,感染者人数达到顶峰, 然后慢慢治愈 , 者就是上图所显示的样子 .
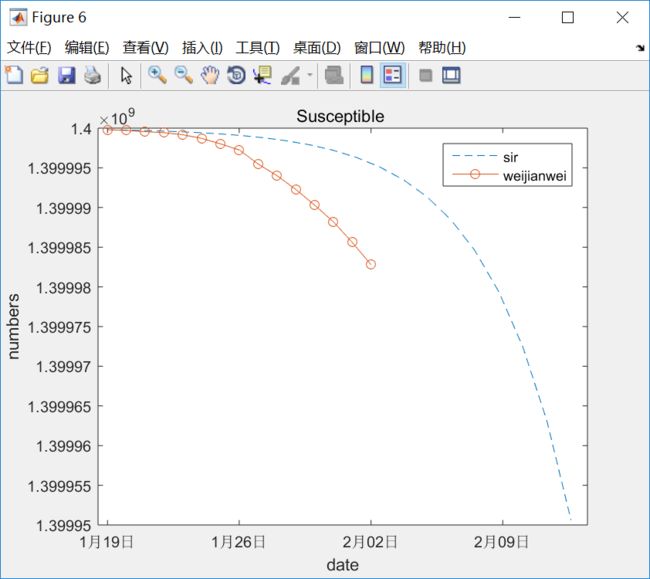
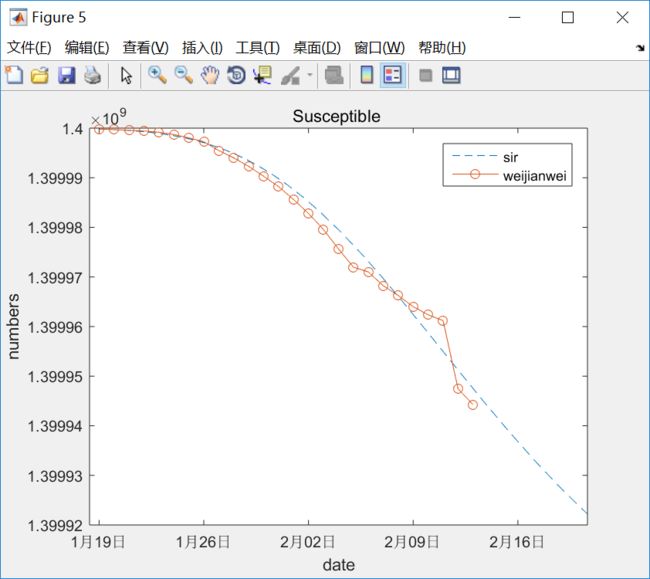
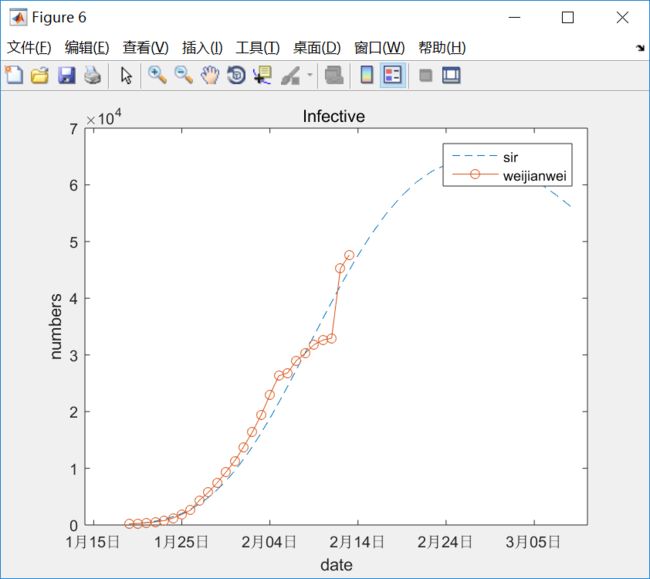
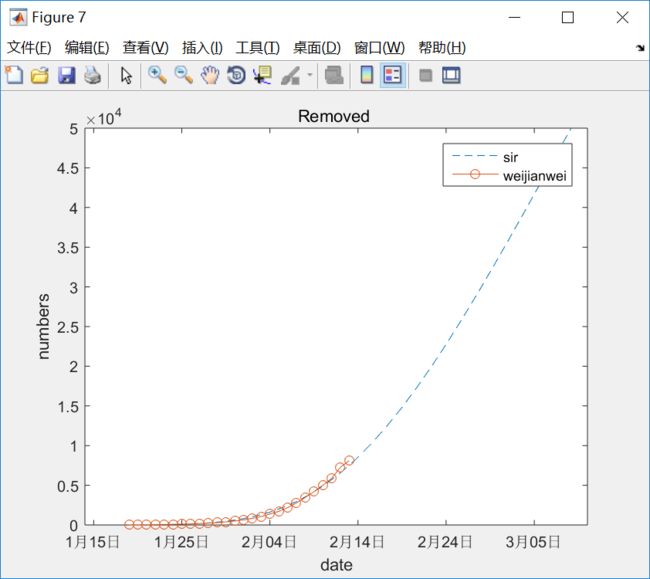
在看看数据拟合的程度怎么呢?
虽然没有做拟合率的量化计算(比如R,假设检验等),目测拟合度是非常低的.
看起来假设lamda 和u为常数是行不通的 ,想别的办法吧 。
3. 带衰减的接触率和治愈率的模型实现
lamda 和u为常数的假设经过截止到2月2日新冠状病毒疫情的数据验证,是失败的,据说在2003年的 非典疫情,这个假设也是失败的。那么lamda 和u也是关于t的函数吗? 根据SIR 常微分方程的(2)(3), 可以用一下公式求出每天的日接触率λ和日治愈率μ,看看他们是不是显得随着时间有规律的变化.
u_t = dR ./ dI
lamda_t = (dI + dR) ./ (I .* S / N)
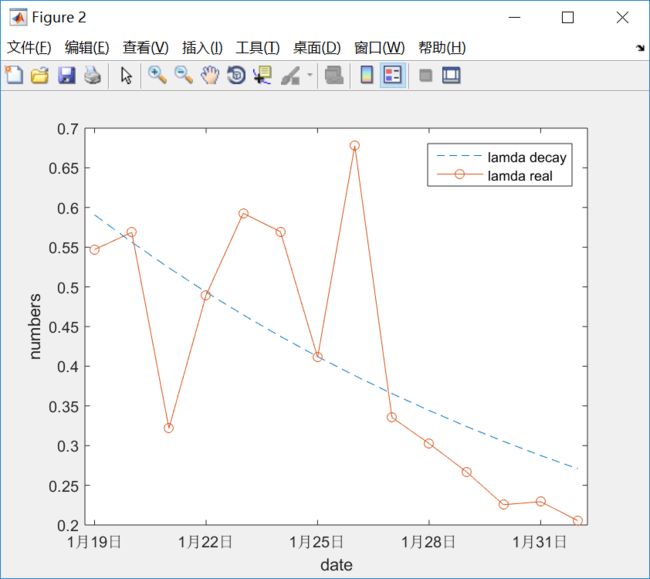
下图黄色线是lamda_t, 蓝色线是有指数函数:a·eb·t , a 和 b 是常数,t 代表从1月19日到改天的天数。虽然拟合也不是很好,感觉上27之前的噪音较大, 27之后有规则的指数形式衰减。尽管受噪音影响,图中的lamda decay 曲线还是比较不错的拟合了lamda随时时间而逐渐衰减的现实。 不过感觉衰减的过快,十几天lamda 衰减为初值的一半,衰减过快会使Infective 曲线机制过早到达。
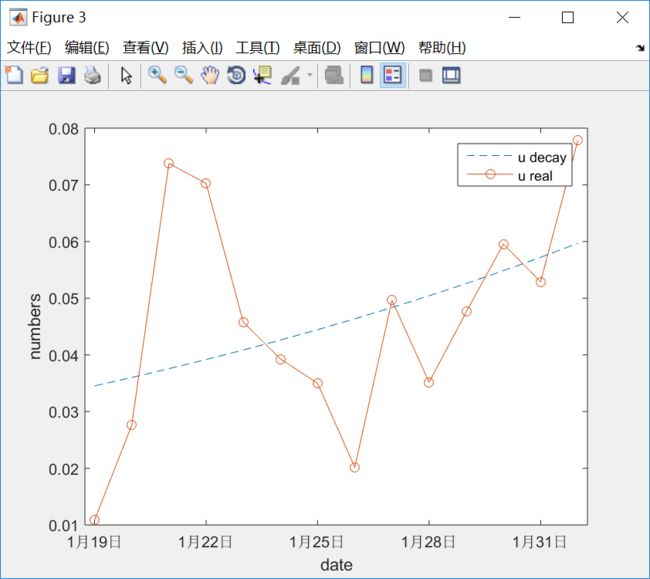
同样的, u_t治愈率 也有随时间以某种指数形式递增的趋势, 但感觉递增的有些快。
逐渐衰减的lamda_t和逐渐上升的u_t, 会使逐步降日低接触率和日治愈率的差距, 减少感染人群的增长趋势, 降低易感人群的感染概率, 降低了I曲线的曲度,从而使极值降低。
下面是部分实现代码
sir_t_run.m :
clear;
global a b N % a,b are the coefficients of decay function of lamda and u
N = 1.4e+9 ;
load('weijianwei');
u_t = dR ./ dI ; % u(t)
lamda_t = (dI + dR) ./ (I .* S / N); %lamda(t)
%plot lamda(t) and u(t)
dates = datetime(Date);
figure;
plot(dates, lamda_t, '--', dates, u_t, '--');
...
% fit lamda(t) using exponential
x0 = [1, 0 ] ;
x = 1:1:length(lamda_t)-1;
a = lsqcurvefit(@decay,x0, x, lamda_t(1:end-1));
...
% fit u(t)
x0 = [1, 0 ] ;
x = 1:1:length(u_t)-1;
b = lsqcurvefit(@decay,x0, x, u_t(1:end-1));
...
% numeric solution of SIR ODE with decayed lamda and decayed u
[t,x]=ode45('sir_t', [0,100], [1399999802 170 28]);
dates=start_date + t;
% plot the the full SIR graph
figure;
plot( dates(1:60), x(1:60,2), '--', dates(1:60), x(1:60,3), '-.k') ;
...
sir_t.m : ode with decayed lamda and u
%S' = -lamda * S * I / N , susceptible
%I' = lamda * S * I /N - u * I , infetive , in hospitable
%R = u * I , recovered or dead , not in hospital
%S +I + R = N
function y=sir_t(t,x)
global a b N
lamda = a(1) * exp( t * a(2));
u = b(1) * exp( t * b(2));
y=[-lamda*x(1)*x(2)/N,lamda*x(1)*x(2)/N-u*x(2), u*x(2)]';
运行一下看看效果吧
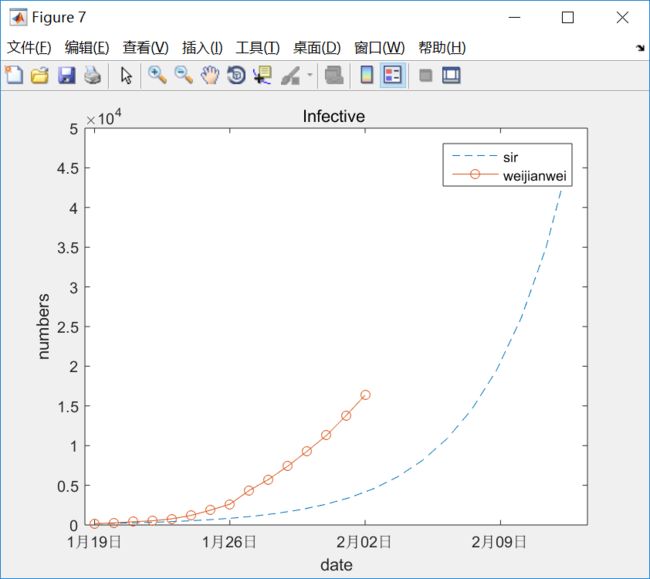
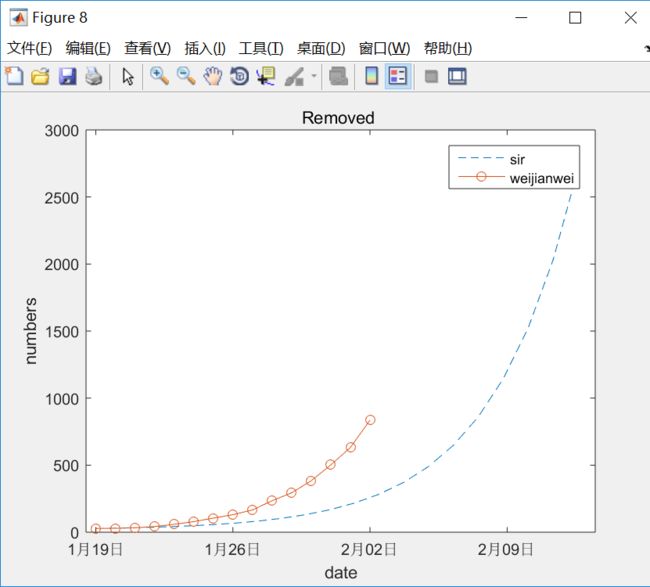
净感染者在2月26左右到达峰值,极值为6.5万左右,加上移除者2.7万左右的移除者,当时的累计确诊应该在9.2万人左右,疫情将在4月底彻底结束。
拟合的效果怎么样呢?还很不错的,所以对上面的预测相对有些信心。
4. SIR模型 变种
卫健委的数据源里还包括了一些重要的公开数据,如疑似病人,医学观察人数,密切接触者,如果能见这个向量加入模型,他们的未来走向,也能反应疫情未来的发展。但是我不是很理解这些数据确切的含义,以及他们之间的关系,所以无法正确的用ODE (常微分方程 )对他们建模 。
比如疑似病人的去向是什么,他来自医院观察者吗?医学观察者是累计量还是净值? 它的去向是什么 ? 它怎么被选中的呢?
我在代码里试着建立一个模型(seir.m)除了SIR 还包含了疑似者(E), 医学观察者(O),结果不怎么合理, 我相信模型是错误的。
但如果能知道他们的正确的定义和他们之间的转化关系, 就可以简历正确的微分方程, 从而建立更完善、更符合新冠状病毒疫情的模型。
SIR还是过于简单, 比如SIR模型假设只有确诊的感染者具有传染性是不准确的, 因为处于潜伏期的疑似病人,医学观察者,密切接触者都可能传染性。如果能将他们加入模型,会更有助于疫情的预测。
5. 本文代码
https://github.com/kaixin1976/coronavirus