分位数回归(quantile regression)R实现
分位数回归(quantile regression)R实现
- 一、基本介绍
- 二、使用分位数回归的原因
- 三、R 语言实现分位数回归
一、基本介绍
回归分析的主要目的:实证检验理论分析中因变量与自变量之间的关系。传统的均值回归,主要使用因变量的条件均值函数来描述在自变量每一个特定数值下的因变量的均值,从而揭示自变量与因变量的关系。
条件均值模型存在不足:当研究收入分配等问题时,我们可能主要关注的是处于分布低尾的穷人和分布高尾的富人等处于因变量非中心位置的情况,而 (1) 条件均值模型主要考虑的是因变量的均值,难以扩展到这种非中心位置,此时只能使用分位数模型进行估计。此外,(2) 条件均值模型经常受到离群值的困扰。在使用条件均值模型进行实证研究时,面对存在离群值的样本数据时,最常使用的方法是对数据进行缩尾,剔除离群值。然而,很多时候剔除离群值会导致对中心位置的测度具有误导性结论。尤其, (3) 条件均值模型假定残差项服从独立同分布、正态性、方差齐性等关键问题在现实中难以满足。
因此,提出了中位数模型替代条件均值模型。中位数是表示分布的中心位置,即0.5分位数。其他位置上的分位数则描述了一种分布的非中心位置。随着协变量的变化,分位数回归模型则强调了条件分位数的变化。由于所有分位数都是可用的,所以对任何预先决定的分布位置进行建模都是可能的。因此,可以对分布的任意非中心位置进行建模,可选的研究的问题也就变得更加广泛。例如贫困问题(对穷人进行研究)、收入分配问题(穷人与富人的收入),教育问题(好成绩与差成绩),税收问题(对穷人与富人的不同影响)等等。与条件均值模型相比,分位数回归则具有无法比拟的优势。
普通最小二乘估计(OLS)与分位数回归估计的异同:

分位数回归是估计一组回归变量X与被解释变量Y的分位数之间线性关系的建模方法。以往的回归模型实际上是研究被解释变量的条件期望。而人们也关心解释变量与被解释变量分布的中位数、分位数呈何种关系。它最早由Koenker和Bassett(1978)提出。
OLS回归估计量的计算是基于最小化残差平方。分位数回归估计量的计算也是基于一种非对称形式的绝对值残差最小化。其中,中位数回归运用的是最小绝对值离差估计(LAD,least absolute deviations estimator)。
分位数回归的优点:
(1) 能够更加全面的描述被解释变量条件分布的全貌,而不是仅仅分析被解释变量的条件期望(均值),也可以分析解释变量如何影响被解释变量的中位数、分位数等。不同分位数下的回归系数估计量常常不同,即解释变量对不同水平被解释变量的影响不同。
(2) 中位数回归的估计方法与最小二乘法相比,估计结果对离群值则表现的更加稳健,而且,分位数回归对误差项并不要求很强的假设条件,因此对于非正态分布而言,分位数回归系数估计量则更加稳健。
目前,分位数回归已经获得了巨大的发展,不仅可以进行简单的横断面数据的估计,而且还可以进行panel数据模型估计、干预效应模型估计、计数模型估计、因变量是区间值的logistic模型估计、工具变量估计等。
二、使用分位数回归的原因
大部分的计量模型都是在估计条件期望值,因为条件期望值是因变量最好的估计值。对于非连续变量,期望值本身已经能够很大程度上描述出随机变量的分布。但是对于连续变量,仅仅依靠期望值并不能完整描述出变量的分布形态。比如收入水平,中位数相比于平均数更有代表性。因为平均数容易受到异常值的影响,如果只考虑平均值,那么穷人就会被富人代表,一个国家的平均收入也许很高,但是这或许只能代表一小部分人,而中位数则能代表大部分普通人的真实收入。
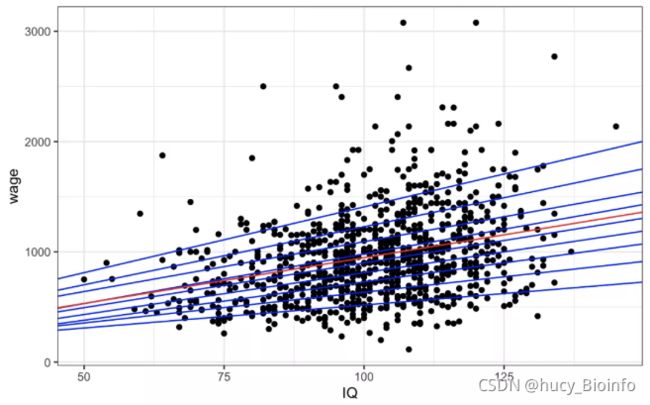
下面这幅散点图反映了个人智商水平(IQ)和收入水平(wage)之间的关系,其中红线就是使用 OLS 进行线性回归得到的,蓝线从上至下依次为 0.9 分位数、中位数、0.1 分位数的回归线。可以发现,对于前 10% 的收入群体,IQ 的增长对收入的边际效应更为明显。所以,使用分位数回归能够更加全面完整的分析因变量的条件分布。

三、R 语言实现分位数回归
R语言进行分位数回归需要quantreg包,其中, rq()函数的用法和 lm() 类似,但是多了一个设定分位数的参数 tau,这个参数可以接受单个值,也可以接受向量值。plot() 函数则可以绘制不同分位数回归的系数值的折线图,和 OLS 线性回归的系数值做比较。
本文使用wooldridgeR包的示例数据集 wage2 进行解释说明,回归的因变量是收入水平 wage ,IQ某种程度上可以指代受访者的个人能力,educ 表示受访者的受教育年限,married 和 black 都分类变量,取值 1 表示受访者分别为已婚和黑裔。
首先只采用 IQ 作为自变量进行回归,分位数选取 [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]。
library(tidyverse)
library(wooldridge)
library(quantreg)
library(AER)
### 查看分布
ggplot(data = wage2, mapping = aes(x = IQ, y = wage)) +
geom_point() +
geom_quantile(quantiles = c(0.1, 0.5, 0.9), size = 1) +
geom_smooth(method = "lm", color = "red", se = F) +
theme_bw()
### OLS回归
wage_lm1 <- lm(wage ~ IQ, data = wage2)
### 分位数回归
wage_qr1 <- rq(wage ~ IQ, data = wage2, tau = 1:9/10)
### OLS回归和分位数回归线
ggplot(data = wage2, aes(x = IQ, y = wage)) +
geom_point() +
geom_abline(intercept = coef(wage_qr1)[1, ], slope = coef(wage_qr1)[2, ], color = "blue") +
geom_abline(intercept = coef(wage_lm1)[1], slope = coef(wage_lm1)[2], color = "red") +
theme_bw()
summary(wage_lm1)
# Call:
# lm(formula = wage ~ IQ, data = wage2)
#
# Residuals:
# Min 1Q Median 3Q Max
# -898.7 -256.5 -47.3 201.1 2072.6
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 116.9916 85.6415 1.366 0.172
# IQ 8.3031 0.8364 9.927 <2e-16 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 384.8 on 933 degrees of freedom
# Multiple R-squared: 0.09554, Adjusted R-squared: 0.09457
# F-statistic: 98.55 on 1 and 933 DF, p-value: < 2.2e-16
summary(wage_qr1)
wage_qr1
# Call:
# rq(formula = wage ~ IQ, tau = 1:9/10, data = wage2)
#
# Coefficients:
# tau= 0.1 tau= 0.2 tau= 0.3 tau= 0.4 tau= 0.5 tau= 0.6 tau= 0.7 tau= 0.8 tau= 0.9
# (Intercept) 100.846154 76.096774 33.333333 52.769231 87.500 81 187.958333 174.81633 214.65517
# IQ 4.173077 5.580645 6.933333 7.576923 8.125 9 9.041667 10.53061 11.93103
#
# Degrees of freedom: 935 total; 933 residual
### 分位数回归和OLS回归系数对比图
plot(summary(wage_qr1), parm = "IQ")
上述回归只有一个变量 IQ,根据分位数回归结果可知,个人能力对收入水平的边际效应对于前 10% 的收入群体更为明显,回归系数的折线图直观反映了这一特点。比如对于 0.9 分位数回归,自变量系数为 11.93103,即个人能力每增长一个单位,0.9 分位数对应的工资水平增长约 11.93。图中的红色直线为 OLS 回归的系数估计值,红色虚线为估计值的置信区间。
下面我们将另外三个变量添加进 OLS 回归和分位数回归,和之前相比,个人能力对收入水平的边际效应有所降低。
wage_lm2 <- lm(wage ~ IQ + educ + married + black, data = wage2)
wage_qr2 <- rq(wage ~ IQ + educ + married + black, data = wage2, tau = 1:9/10)
summary(wage_lm2)
# Call:
# lm(formula = wage ~ IQ + educ + married + black, data = wage2)
#
# Residuals:
# Min 1Q Median 3Q Max
# -853.23 -247.90 -27.76 186.07 2081.80
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) -196.726 106.521 -1.847 0.06509 .
# IQ 3.944 1.002 3.935 8.94e-05 ***
# educ 44.472 6.446 6.899 9.68e-12 ***
# married 192.749 39.307 4.904 1.11e-06 ***
# black -124.086 39.344 -3.154 0.00166 **
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 370 on 930 degrees of freedom
# Multiple R-squared: 0.1662, Adjusted R-squared: 0.1626
# F-statistic: 46.34 on 4 and 930 DF, p-value: < 2.2e-16
summary(wage_qr2)
wage_qr2
# Call:
# rq(formula = wage ~ IQ + educ + married + black, tau = 1:9/10,
# data = wage2)
#
# Coefficients:
# tau= 0.1 tau= 0.2 tau= 0.3 tau= 0.4 tau= 0.5 tau= 0.6 tau= 0.7 tau= 0.8 tau= 0.9
# (Intercept) 30.00 -104.717514 -120.538462 -121.4 -168.230769 -206.190476 -254.484848 -380.45455 -476.949275
# IQ 2.00 3.028249 3.769231 3.6 4.153846 3.539683 4.139394 5.69697 6.963768
# educ 16.25 26.683616 26.038462 33.6 38.230769 50.333333 56.842424 60.94444 76.550725
# married 94.00 126.559322 161.692308 168.0 194.769231 222.126984 221.018182 238.93939 180.311594
# black -74.00 -97.502825 -103.730769 -94.6 -118.846154 -141.809524 -141.521212 -124.66667 -37.985507
#
# Degrees of freedom: 935 total; 930 residual
plot(summary(wage_qr2), parm = c("IQ", "educ", "married", "black"))

根据回归系数的折线图我们可知,educ对收入水平的边际效应随着分位数的增加而增加,也就是说对于高收入群体其边际效应更大一些。IQ 代表的个人能力虽然有所波动,但整体随着分位数向上。married 婚姻状态比较有意思的是对于处于社会财富前 10% 的收入群体,其边际效应并不是最高的。联想到前段时间离婚的某些富豪,好像也就不难理解了。black 的分位数回归系数曲线是这四个变量中最为特殊的,不论处于哪一个收入水平段,黑人族裔身份都会带来负面影响,并且在中产阶级中最为显著。
参考阅读:
【R语言】横截面数据分位数回归简介
【R语言】生存分析, 用R语言进行分位数回归(Quantile Regression)
【Stata+R】分位数回归一文读懂
【Stata】分位数回归
【Stata】qregplot:分位数回归图示
【SPSS】分位数回归[Quantile regression]