手写算法-python代码实现Lasso回归

Lasso回归简介

上一篇文章我们详细介绍了过拟合和L1、L2正则化，Lasso就是基于L1正则化，它可以使得参数稀疏，防止过拟合。其中的原理都讲的很清楚，详情可以看我的这篇文章。
链接: 原理解析-过拟合与正则化

本文主要实现python代码的Lasso回归，并用实例佐证原理。

Lasso回归分析与python代码实现

我们先生成数据集，还是用sklearn生成。

import numpy as np
from matplotlib import pyplot as plt
import sklearn.datasets

#生成100个一元回归数据集
x,y = sklearn.datasets.make_regression(n_features=1,noise=5,random_state=2020)
plt.scatter(x,y)
plt.show()

如上所示，生成了一个一元回归数据集，如果数据中混入了噪声，如：（手动添加5个噪声数据）

#加5个异常数据,为什么这么加，大家自己看一下生成的x,y的样子
a = np.linspace(1,2,5).reshape(-1,1)
b = np.array([350,380,410,430,480])

#生成新的数据集
x_1 = np.r_[x,a]
y_1 = np.r_[y,b]

plt.scatter(x_1,y_1)
plt.show()

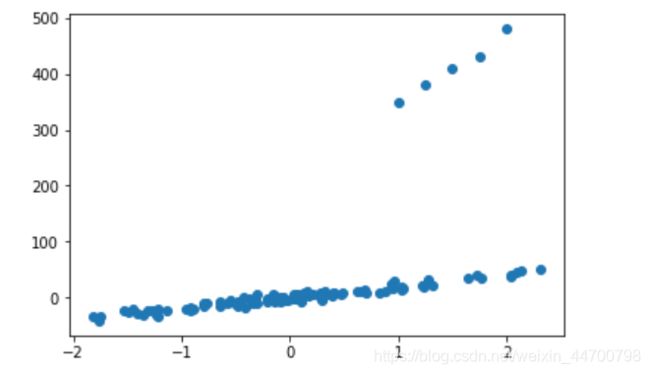
这个时候，数据表现为这个样子，由于这几个数据是异常数据，所以我们的线性回归模型应该拟合下面的样本点，即最终的参数应该比较小，不应该因为加入了几个很异常的数据，导致参数发生很大的偏移，以这个图为例，就是不应该变得很大。
，下面用我们之前写好的线性回归类（python代码实现），来展示效果：

class normal():
    def __init__(self):
        pass

    def fit(self,x,y):
        m=x.shape[0]
        X = np.concatenate((np.ones((m,1)),x),axis=1)
        xMat=np.mat(X)
        yMat =np.mat(y.reshape(-1,1))

        xTx=xMat.T*xMat
        #xTx.I为xTx的逆矩阵
        ws=xTx.I*xMat.T*yMat
        
        #返回参数
        return ws
         


plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
clf1 =normal()
#拟合原始数据
w1 = clf1.fit(x,y)
#预测数据
y_pred = x * w1[1] + w1[0]

#拟合新数据
w2 = clf1.fit(x_1,y_1)
#预测数据
y_1_pred = x_1 * w2[1] + w2[0]

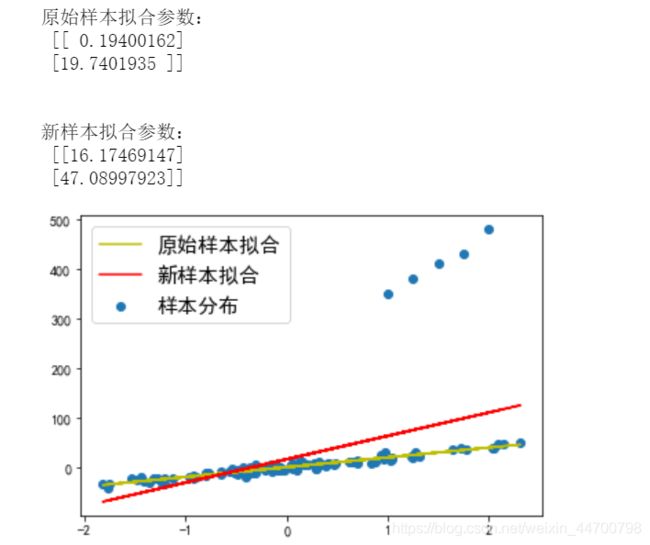
print('原始样本拟合参数：\n',w1)
print('\n')
print('新样本拟合参数：\n',w2)

ax1= plt.subplot()
ax1.scatter(x_1,y_1,label='样本分布')
ax1.plot(x,y_pred,c='y',label='原始样本拟合')
ax1.plot(x_1,y_1_pred,c='r',label='新样本拟合')
ax1.legend(prop = {'size':15}) #此参数改变标签字号的大小
plt.show()

W的第一个参数是截距，第二个参数是斜率，也就是系数，可以看到系数变大了很多，仅因为加入了几个噪声，模型的鲁棒性很差，泛化能力也差，出现了一定程度的过拟合。

我们再来看Lasso的表达式：

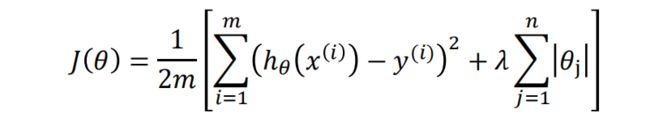
= 线性回归损失函数 + L1正则项，上一篇文章我们有分析过L1正则项的特点（本文前面有链接），参数λ是正则项系数，正则项对参数θ不是连续可导，一般情况下，有以下两种方式来求Lasso的参数，
1、坐标轴下降法
2、用最小角回归法
这里推荐一篇刘建平博士的博客，写得很清楚。
链接: Lasso回归算法： 坐标轴下降法与最小角回归法小结

1、python实现坐标轴下降法求解Lasso

我们采用坐标轴下降法来求参数：python代码实现如下：

#临时写的函数，要在引入一个copy包，进行深度拷贝
#大家写一份代码，把要引入的包全放在最前面
import copy

 def CoordinateDescent(x, y,epochs,learning_rate,Lambda):        
        m=x.shape[0]
        X = np.concatenate((np.ones((m,1)),x),axis=1)
        xMat=np.mat(X)
        yMat =np.mat(y.reshape(-1,1))
        
        
        w = np.ones(X.shape[1]).reshape(-1,1)
        
        
        for n in range(epochs):
            
            
            out_w = copy.copy(w)
            for i,item in enumerate(w):
                #在每一个W值上找到使损失函数收敛的点
                for j in range(epochs):
                    h = xMat * w 
                    gradient = xMat[:,i].T * (h - yMat)/m + Lambda * np.sign(w[i])
                    w[i] = w[i] - gradient* learning_rate
                    if abs(gradient)<1e-3:
                        break
            out_w = np.array(list(map(lambda x:abs(x)<1e-3, out_w-w)))
            if out_w.all():
                break
        return  w

CoordinateDescent()函数来实现我们的Lasso回归，示例：

当Lambda参数为0时，也就是不加L1正则项时，就是普通的线性回归，参数输出都是一样的，也是47点多

#Lambda=0时；
w = CoordinateDescent(x_1,y_1,epochs=250,learning_rate=0.001,Lambda=0)
print(w)

#计算新的拟合值
y_1_pred = x_1 * w[1] + w[0]

ax1= plt.subplot()
ax1.scatter(x_1,y_1,label='样本分布')
ax1.plot(x,y_pred,c='y',label='原始样本拟合')
ax1.plot(x_1,y_1_pred,c='r',label='新样本拟合')
ax1.legend(prop = {'size':15}) #此参数改变标签字号的大小
plt.show()

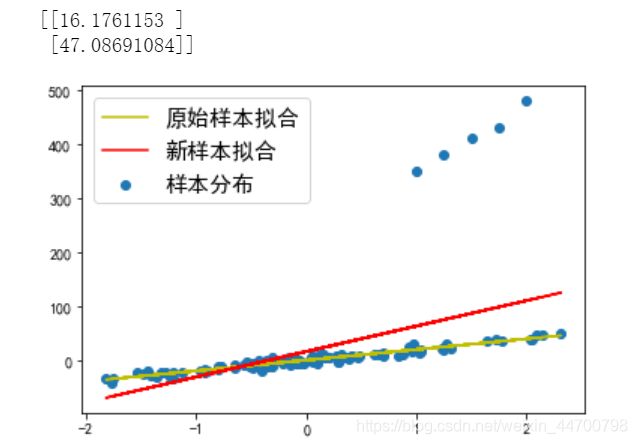
当Lambda =10时，参数变为37点多；

#Lambda=10时；
w = CoordinateDescent(x_1,y_1,epochs=250,learning_rate=0.001,Lambda=10)
print(w)

#计算新的拟合值
y_1_pred = x_1 * w[1] + w[0]

ax1= plt.subplot()
ax1.scatter(x_1,y_1,label='样本分布')
ax1.plot(x,y_pred,c='y',label='原始样本拟合')
ax1.plot(x_1,y_1_pred,c='r',label='新样本拟合')
ax1.legend(prop = {'size':15}) #此参数改变标签字号的大小
plt.show()

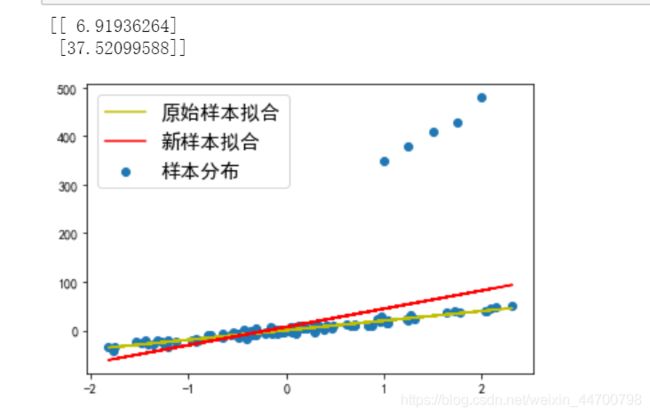
当Lambda =30时，参数变为17点多，基本上已经和没添加异常值的参数是一样的了；

#Lambda=30时；
w = CoordinateDescent(x_1,y_1,epochs=250,learning_rate=0.001,Lambda=30)
print(w)

#计算新的拟合值
y_1_pred = x_1 * w[1] + w[0]

ax1= plt.subplot()
ax1.scatter(x_1,y_1,label='样本分布')
ax1.plot(x,y_pred,c='y',label='原始样本拟合')
ax1.plot(x_1,y_1_pred,c='r',label='新样本拟合')
ax1.legend(prop = {'size':15}) #此参数改变标签字号的大小
plt.show()

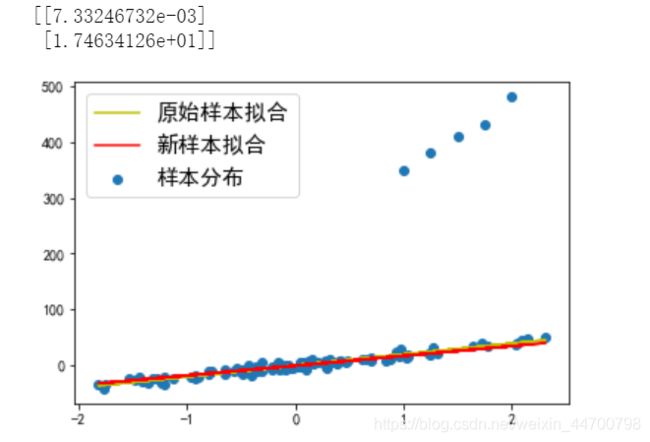
当Lambda =100时，参数基本上已经趋近于0，拟合线差不多就是一条水平线了；

#Lambda=100时；
w = CoordinateDescent(x_1,y_1,epochs=250,learning_rate=0.001,Lambda=100)
print(w)

#计算新的拟合值
y_1_pred = x_1 * w[1] + w[0]

ax1= plt.subplot()
ax1.scatter(x_1,y_1,label='样本分布')
ax1.plot(x,y_pred,c='y',label='原始样本拟合')
ax1.plot(x_1,y_1_pred,c='r',label='新样本拟合')
ax1.legend(prop = {'size':15}) #此参数改变标签字号的大小
plt.show()

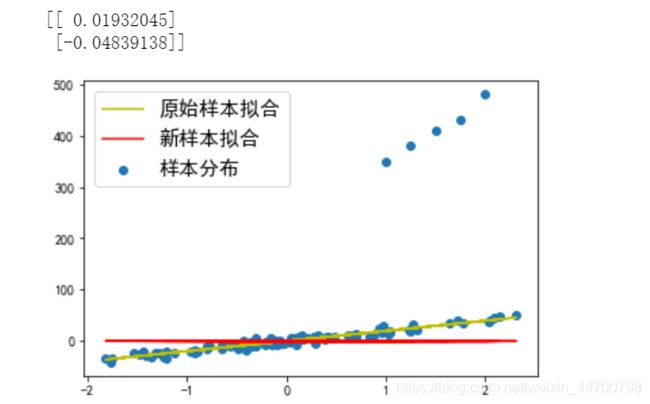
正则项参数过大、过小都不好，
过小起不到惩罚效果，模型任然过拟合；
过大惩罚太大，会使得模型欠拟合，达不到要求；
我们选择参数的标准：模型在训练集、验证集、测试集上，评估效果接近时，这个正则项参数较好。

调用sklearn的Lasso回归对比

同样的，可以调用sklearn的Lasso回归来测试代码的正确性；
（只看参数的值，图就不画了）

from sklearn.linear_model import Lasso
lr=Lasso(alpha=0)
lr.fit(x_1,y_1)
print('alpha=0时',lr.coef_,'\n')

lr=Lasso(alpha=10)
lr.fit(x_1,y_1)
print('alpha=10时',lr.coef_,'\n')

lr=Lasso(alpha=30)
lr.fit(x_1,y_1)
print('alpha=30时',lr.coef_,'\n')

lr=Lasso(alpha=100)
lr.fit(x_1,y_1)
print('alpha=100时',lr.coef_)

基本上和我们的python代码实现的系数差不多。

2、近似梯度下降法python代码实现Lasso

只是在我们梯度下降法代码基础上，改了梯度的计算，加了sign(w)，也就是加上L1正则项的导数）；

class lasso():
    def __init__(self):
        pass
    
    #梯度下降法迭代训练模型参数,x为特征数据，y为标签数据，a为学习率，epochs为迭代次数
    def fit(self,x,y,a,epochs,Lambda):  
        #计算总数据量
        m=x.shape[0]
        #给x添加偏置项
        X = np.concatenate((np.ones((m,1)),x),axis=1)
        #计算总特征数
        n = X.shape[1]
        #初始化W的值,要变成矩阵形式
        W=np.mat(np.ones((n,1)))
        #X转为矩阵形式
        xMat = np.mat(X)
        #y转为矩阵形式，这步非常重要,且要是m x 1的维度格式
        yMat =np.mat(y.reshape(-1,1))
        #循环epochs次
        for i in range(epochs):
            gradient = xMat.T*(xMat*W-yMat)/m + Lambda * np.sign(W)
            W=W-a * gradient
        return W
    def predict(self,x,w):  #这里的x也要加偏置，训练时x是什么维度的数据，预测也应该保持一样
        return np.dot(x,w)

下面是运行的结果:

sklearn展示Lasso：

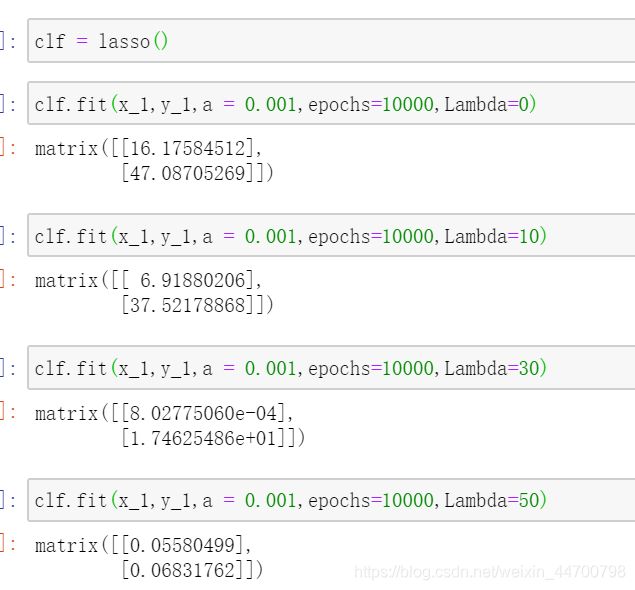
1、随着alpha值的增大，也就是正则项系数增大，系数变得越来越稀疏，更多的系数变为0。

#波士顿房价回归数据集
data =  sklearn.datasets.load_boston()
x =data['data']
y= data['target']

from sklearn.linear_model import Lasso
lr=Lasso(alpha= 1)
lr.fit(x,y)
print('当alpha=1时：\n',lr.coef_)

lr=Lasso(alpha= 5)
lr.fit(x,y)
print('当alpha=5时：\n',lr.coef_)

lr=Lasso(alpha= 10)
lr.fit(x,y)
print('当alpha=10时：\n',lr.coef_)

下一篇我们介绍Ridge回归。