回归——一元线性回归
一元线性回归
- 基本概念
-
- 分类与回归
- 一元线性回归
-
- 代价函数
- 相关系数
- 梯度下降法
- 推导
- 代码实现
-
- 梯度下降法Python代码实现
-
- 从0开始
- 借助python库
- matlab代码实现
- 参考文章链接
基本概念
分类与回归
什么叫做回归?回归是相对分类而言的,与我们想要预测的目标变量y的值类型有关。《统计学习》一书中指出,人们常根据输入输出变量的不同类型,对预测任务给予不同的名称:输入变量与输出变量均为连续变量的预测问题称为回归问题;输出变量为有限个离散变量的预测问题称为分类问题。
什么叫做线性回归?线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。
一元线性回归与多元线性回归的定义:只有一个自变量的情况称为单变量回归,多于一个自变量情况的叫做多元回归。
多元回归的通用形式: w 1 x 1 + w 2 x 2 + . . . + w d x d + b = f ( x ) {w_1}{x_1} + {w_2}{x_2} + ... + {w_d}{x_d} + b = f(x) w1x1+w2x2+...+wdxd+b=f(x)
多元回归的向量形式: ω T x + b = f ( x ) {\omega ^{\rm T}}x + b = f(x) ωTx+b=f(x) , 其中 ω = ( ω 1 ; ω 2 ; ⋯ ; ω d ; ) \omega = ({\omega _1};{\omega _2}; \cdots ;{\omega _d};) ω=(ω1;ω2;⋯;ωd;)
关于分类和回归的举例:y是分类型变量,如预测用户的性别(男、女),预测月季花的颜色(红、白、黄……),预测是否患有肺癌(是、否),那我们就需要用分类算法去拟合训练数据并做出预测;y是连续型变量,如预测用户的收入(4千,2万,10万……),预测员工的通勤距离(500m,1km,2万里……),预测患肺癌的概率(1%,50%,99%……),我们则需要用回归模型。
有时分类问题也可以转化为回归问题,例如刚刚举例的肺癌预测,我们可以用回归模型先预测出患肺癌的概率,然后再给定一个阈值,例如50%,概率值在50%以下的人划为没有肺癌,50%以上则认为患有肺癌。这种分类型问题的回归算法预测,最常用的就是逻辑回归,后面会总结到。
线性回归当中主要有两种模型,一种是线性关系,另一种是非线性关系。在这里我们只能画一个平面更好去理解,所以都用单个特征或两个特征举例子。
 图1 单变量线性关系 图1 单变量线性关系
|
 图2 多变量线性关系 图2 多变量线性关系
|
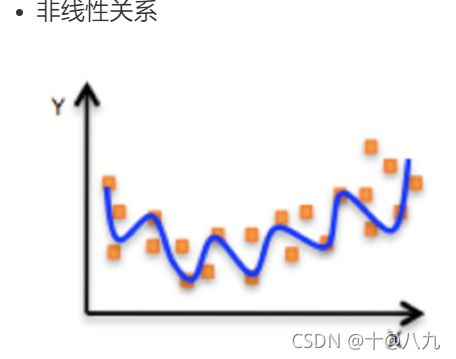 图3 非线性关系 图3 非线性关系
|
一元线性回归
h θ ( x ) = θ 0 + θ 1 x {h_\theta }(x) = {\theta _0} + {\theta _1}x hθ(x)=θ0+θ1x
这个方程对应的图像是一条直线,称作回归线。其中, θ 1 {\theta _1} θ1为回归线的斜率, θ 0 {\theta _0} θ0为回归线的截距。此时,
θ 1 {\theta _1} θ1 > 0时,一元线性回归 正相关;
θ 1 {\theta _1} θ1 < 0时,一元线性回归 负相关;
θ 1 {\theta _1} θ1 = 0时,一元线性回归 不相关;
代价函数
- 最小二乘法
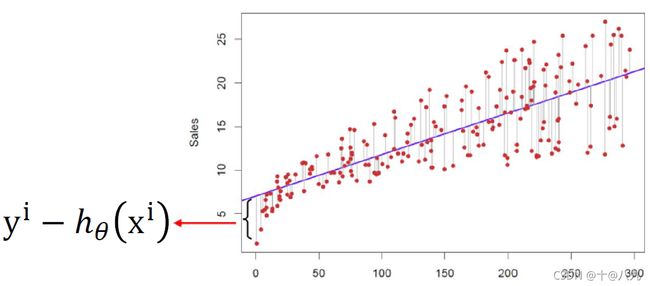
- 真实值y,预测值 h θ ( x ) {h_\theta }(x) hθ(x),误差平方为 ( y − h θ ( x ) ) 2 {(y - {h_\theta }(x))^2} (y−hθ(x))2
- 找到合适的参数,使得误差平方和: J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( y i − h θ ( x i ) ) 2 J({\theta _0},{\theta _1}) = \frac{1}{{2m}}\sum\nolimits_{i = 1}^m {{{({y^i} - {h_\theta }({x^i}))}^2}} J(θ0,θ1)=2m1∑i=1m(yi−hθ(xi))2 最小
相关系数
我们一般使用相关系数去衡量线性关系的强弱: r x y = ∑ ( X i − X ˉ ) ( Y i − Y ˉ ) ∑ ( X i − X ˉ ) 2 ∑ ( Y i − Y ˉ ) 2 {r_{xy}} = \frac{{\sum {({X_i} - \bar X)({Y_i} - \bar Y)} }}{{\sqrt {\sum {{{({X_i} - \bar X)}^2}\sum {{{({Y_i} - \bar Y)}^2}} } } }} rxy=∑(Xi−Xˉ)2∑(Yi−Yˉ)2∑(Xi−Xˉ)(Yi−Yˉ)
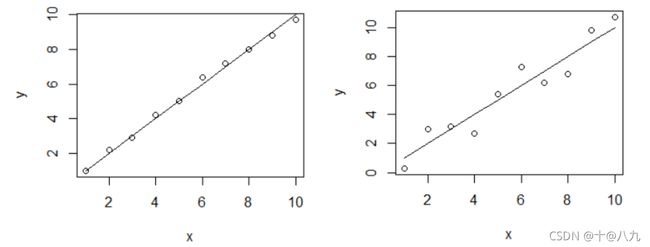
通过计算,左图的相关系数为0.993 ,右图的相关系数为 0.957。
相关系数(coefficient of (coefficient of)是用来描述两个变量之间的线性关系的,但决定系数的适用范围更广,可以用于描述非线性或者有两个及两个以上自变量的相关关系。它可以用来评价模型的效果。
总平方和(SST): ∑ i = 1 n ( y i − y ˉ ) 2 {\sum\nolimits_{i = 1}^n {({y_i} - \bar y)} ^2} ∑i=1n(yi−yˉ)2
回归平方和(SSR): ∑ i = 1 n ( y ^ i − y ˉ ) 2 {\sum\nolimits_{i = 1}^n {({{\hat y}_i} - \bar y)} ^2} ∑i=1n(y^i−yˉ)2
残差平方和(SSE): ∑ i = 1 n ( y ^ i − y ^ ) 2 {\sum\nolimits_{i = 1}^n {({{\hat y}_i} - \hat y)} ^2} ∑i=1n(y^i−y^)2
它们三者之间的关系是:SST=SSR+SSE
决定系数: R 2 = S S R S S T = 1 − S S E S S T R2 = \frac{{SSR}}{{SST}} = 1 - \frac{{SSE}}{{SST}} R2=SSTSSR=1−SSTSSE
梯度下降法
简单得说,就是存在一个函数 J ( θ 0 , θ 1 ) J({\theta _0},{\theta _1}) J(θ0,θ1),想取到 min θ 0 , θ 1 J ( θ 0 , θ 1 ) \mathop {\min }\limits_{{\theta _0},{\theta _1}} J({\theta _0},{\theta _1}) θ0,θ1minJ(θ0,θ1),那么,我们该如何做呢?
- 初始化 ( θ 0 , θ 1 ) ({\theta _0},{\theta _1}) (θ0,θ1)
- 不断改变 ( θ 0 , θ 1 ) ({\theta _0},{\theta _1}) (θ0,θ1),直到 J ( θ 0 , θ 1 ) J({\theta _0},{\theta _1}) J(θ0,θ1)到达一个全局最小值,或局部极小值。即, θ j : = θ j − α ∂ ∂ θ j ( θ 0 , θ 1 ) {\theta _j}: = {\theta _j} - \alpha \frac{\partial }{{\partial {\theta _j}}}({\theta _0},{\theta _1}) θj:=θj−α∂θj∂(θ0,θ1) for(j=0 and j=1)
注:学习率不能太小,也太能太大。

|

|
正确做法:同步更新
t e m p 0 : = θ 0 − α ∂ ∂ θ 0 J ( θ 0 , θ 1 ) temp0: = {\theta _0} - \alpha \frac{\partial }{{\partial {\theta _0}}}J({\theta _0},{\theta _1}) temp0:=θ0−α∂θ0∂J(θ0,θ1)
t e m p 1 : = θ 1 − α ∂ ∂ θ 1 J ( θ 0 , θ 1 ) temp1: = {\theta _1} - \alpha \frac{\partial }{{\partial {\theta _1}}}J({\theta _0},{\theta _1}) temp1:=θ1−α∂θ1∂J(θ0,θ1)
θ 0 : = t e m p 0 {\theta _0}: = temp0 θ0:=temp0
θ 1 : = t e m p 1 {\theta _1}: = temp1 θ1:=temp1
不正确做法:
t e m p 0 : = θ 0 − α ∂ ∂ θ 0 J ( θ 0 , θ 1 ) temp0: = {\theta _0} - \alpha \frac{\partial }{{\partial {\theta _0}}}J({\theta _0},{\theta _1}) temp0:=θ0−α∂θ0∂J(θ0,θ1)
θ 0 : = t e m p 0 {\theta _0}: = temp0 θ0:=temp0
t e m p 1 : = θ 1 − α ∂ ∂ θ 1 J ( θ 0 , θ 1 ) temp1: = {\theta _1} - \alpha \frac{\partial }{{\partial {\theta _1}}}J({\theta _0},{\theta _1}) temp1:=θ1−α∂θ1∂J(θ0,θ1)
θ 1 : = t e m p 1 {\theta _1}: = temp1 θ1:=temp1
推导
用梯度下降法求解线性回归
线性回归的模型和代价函数:
- h θ ( x ) = θ 0 + θ 1 x {h_\theta }(x) = {\theta _0} + {\theta _1}x hθ(x)=θ0+θ1x
- J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) J({\theta _0},{\theta _1}) = \frac{1}{{2m}}\sum\limits_{i = 1}^m {({h_\theta }({x^{(i)}}) - {y^{(i)}})} J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))
∂ ∂ θ j J ( θ 0 , θ 1 ) = \frac{\partial }{{\partial {\theta _j}}}J({\theta _0},{\theta _1}) = ∂θj∂J(θ0,θ1)=
j = 0 : ∂ ∂ θ 0 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) j = 0:\frac{\partial }{{\partial \theta 0}}J({\theta _0},{\theta _1}) = \frac{1}{m}\sum\limits_{i = 1}^m {({h_\theta }({x^{(i)}}) - {y^{(i)}}) } j=0:∂θ0∂J(θ0,θ1)=m1i=1∑m(hθ(x(i))−y(i))
j = 1 : ∂ ∂ θ 1 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) j = 1:\frac{\partial }{{\partial \theta 1}}J({\theta _0},{\theta _1}) = \frac{1}{m}\sum\limits_{i = 1}^m {({h_\theta }({x^{(i)}}) - {y^{(i)}}) \cdot {x^{(i)}}} j=1:∂θ1∂J(θ0,θ1)=m1i=1∑m(hθ(x(i))−y(i))⋅x(i)
repeat until convergence{
θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) {\theta _0}: = {\theta _0} - \alpha \frac{1}{m}\sum\limits_{i = 1}^m {({h_\theta }({x^{(i)}}) - {y^{(i)}})} θ0:=θ0−αm1i=1∑m(hθ(x(i))−y(i))
θ 1 : = θ 1 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) {\theta _1}: = {\theta _1} - \alpha \frac{1}{m}\sum\limits_{i = 1}^m {({h_\theta }({x^{(i)}}) - {y^{(i)}})} \cdot {x^{(i)}} θ1:=θ1−αm1i=1∑m(hθ(x(i))−y(i))⋅x(i)
}
代码实现
梯度下降法Python代码实现
从0开始
import numpy as np
import matplotlib.pyplot as plt
from pylab import mpl
# 设置显示中文字体
mpl.rcParams["font.sans-serif"] = ["SimHei"]
# 设置正常显示符号
mpl.rcParams["axes.unicode_minus"] = False
# 载入数据
data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:, 0]
y_data = data[:, 1]
plt.scatter(x_data, y_data)
plt.savefig('./imgs/数据分布图.jpg')
plt.show()
# 学习率learning rate
lr = 0.0001
# 截距
b = 0
# 斜率
k = 0
# 最大迭代次数
epochs = 50
# 最小二乘法
def compute_error(b, k, x_data, y_data):
totalError = 0
for i in range(0, len(x_data)):
totalError += (y_data[i] - (k * x_data[i] + b)) ** 2
return totalError / float(len(x_data)) / 2.0
def gradient_descent_runner(x_data, y_data, b, k, lr, epochs):
# 计算总数据量
m = float(len(x_data))
# 循环epochs次
for i in range(epochs):
b_grad = 0
k_grad = 0
# 计算梯度的总和再求平均
for j in range(0, len(x_data)):
b_grad += (1 / m) * (((k * x_data[j]) + b) - y_data[j])
k_grad += (1 / m) * x_data[j] * (((k * x_data[j]) + b) - y_data[j])
# 更新b和k
b = b - (lr * b_grad)
k = k - (lr * k_grad)
# 每迭代5次,输出一次图像
if i % 5 == 0:
print("epochs:", i)
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, k * x_data + b, 'r')
plt.xlabel("x")
plt.ylabel("y")
plt.title('迭代%s次的线性回归'%(i))
plt.savefig('./imgs/迭代%s次的线性回归.jpg' %(i))
plt.show()
return b, k
print("Starting b = {0}, k = {1}, error = {2}".format(b, k, compute_error(b, k, x_data, y_data)))
print("Running...")
b, k = gradient_descent_runner(x_data, y_data, b, k, lr, epochs)
print("After {0} iterations b = {1}, k = {2}, error = {3}".format(epochs, b, k, compute_error(b, k, x_data, y_data)))
# 画图
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, k*x_data + b, 'r')
plt.xlabel("x")
plt.ylabel("y")
plt.title('迭代50次的线性回归')
plt.savefig('./imgs/迭代50次的线性回归.jpg')
plt.show()
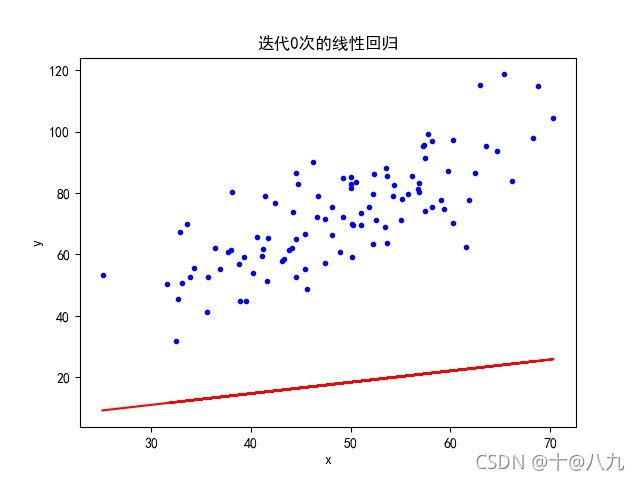 图1 迭代0次 图1 迭代0次
|
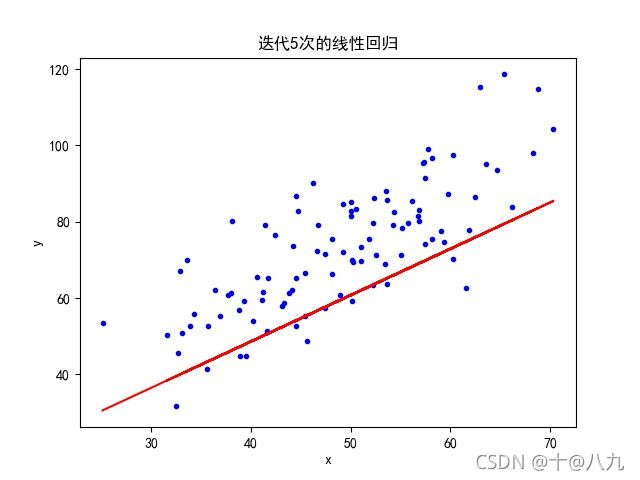 图2 迭代5次 图2 迭代5次
|
 图3 迭代15次 图3 迭代15次
|
 图4 迭代50次 图4 迭代50次
|
参考bilibili: https://www.bilibili.com/video/BV1Rt411q7WJ?p=7
借助python库
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
from pylab import mpl
# 设置显示中文字体
mpl.rcParams["font.sans-serif"] = ["SimHei"]
# 载入数据
data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:, 0]
y_data = data[:, 1]
plt.scatter(x_data, y_data)
plt.show()
print(x_data.shape)
x_data = data[:, 0, np.newaxis]
y_data = data[:, 1, np.newaxis]
# 创建并拟合模型
model = LinearRegression()
model.fit(x_data, y_data)
# 画图
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, model.predict(x_data), 'r')
plt.xlabel("x_data")
plt.ylabel("y_data")
plt.title('sklearn——一元线性回归')
plt.savefig('./imgs/sklearn——一元线性回归.jpg')
plt.show()
# 系数(可理解为斜率)
print('系数:', model.coef_)
# 截距
print('截距:', model.intercept_)
# 决定系数 R2→1模型的数据拟合性就越好,反之,R2→0,表明模型的数据拟合度越差。
print('决定系数:', model.score(x_data, y_data))
matlab代码实现
参考文章链接
参考1: https://www.bilibili.com/video/BV1Rt411q7WJ?p=7
参考2: https://zhuanlan.zhihu.com/p/72513104

