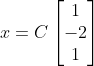矩阵的投影、线性拟合与最小二乘法

概要：投影矩阵

        

      如果一个b向量进行矩阵运算  Pb  , 那么向量b就会投影要A的列空间的最近点。

       

目录

一、矩阵的四大基础子空间

二、投影矩阵

三、最小二乘法

---

一、矩阵的四大基础子空间

        一个矩阵有4个子空间。分别是行空间、零空间、列空间和左零空间(A转置的零空间).所谓A矩阵的行空间就是矩阵的行向量的线性组合，它与零空间正交(即向量垂直，内积为0)。A矩阵的列空间就是矩阵列向量的线性组合，它与左零空间正交。

对于一个初等矩阵E，如果满足 EA=B,那么B的每个行向量都是A行向量的线性组合,A的行向量也是B行向量的线性组合，即A和B的行空间是一样的，并且Ax=0 与 Bx=0的解也是相同的,即A与B的零空间相同。同理，如果AE=B那么A与B有相同的列空间和左零空间。

 零空间该如何求出来的，最简单的就是化成最简式

例如 存在一个初等矩阵E，化成最简式EA=R， 

A，R拥有相同的行空间，即每行都是 (1,2,3)与(4,5,6)的线性组合，同时也是(1,0,-1)与(0,1,2)的线性组合。

对于 RX=0 可以求得 x的通解为

因此零空间就是(1,-2,1)的线性组合，它与矩阵A和R的行向量乘积都为0，即零空间与行空间正交。 此矩阵的行空间由两个互不相关的向量任意倍数组合而成，也就是行向量的基，可以看出行秩为2，即行空间的维度是2，零空间的维度是1。同理，对于左零空间的求法，就是对A进行转置，后面用相同的处理方法就可以的出来。

实际上，对于一个m行*n列的矩阵，4大子空间的维度有如下关系：如果矩阵A的列空间的维数是r，那么A的行空间的维数也是r，零空间 N(A) 的维数是n-r，左零空间 N(A) 的维数是m-r.

二、投影矩阵

在投影矩阵前，要先要了解向量怎么投影。就是在向量的终点处做一个垂线，垂直于要投影到的空间上。例如一个(1,2,3)的向量投影到x轴上就是(1,0,0)，垂直的向量e为(0,2,3)，投影到y轴上就是(0,2,0),e为(1,0,3)，投影到xy平面上就是(1,2,0),e为(0,0,3)。

假设矩阵A有一个向量b在矩阵A的列空间上的投影为向量p，那么法向量就是 e=b-p存在一个投影矩阵P满足Pb=p,

对于  Ax=b ，假如有解，则b向量就是在A的列空间上，b投影到A的列空间就是b向量自己。如果Ax=b无解，也就是说b向量不在A的列空间上，但是可以有一个投影矩阵P，使向量b在A的列空间上的投影为p，有最优解即，

因为e垂直于平面A的列空间,，所以 e在A的左零空间中，即，其中e = b - p 

因此得出    通过移项得到 

所以   ， 其中b的系数部分称之为投影矩阵

小知识：

用相同的投影矩阵投影多次，则相当于投影一次，即 。

对于Ax=b，如果b向量原来就在A的列空间上，那么p和b相同；如果b与A的列空间正交，那么p就是零向量。

三、最小二乘法

假如 Ax=b无解，但是我们可以求出b在A列空间上的最优解，因此最小二乘法实际上就是求最优解，其原理就是空间投影

即   

例如在二维平面上有3个点(1,1) (2,2) ,(3,2)，求一个直线函数 f(x)=ax +b 满足过那3个点的最优解。

有三个方程,两个未知数

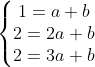   化成矩阵形式  Ax=b 为 ,此方程式无解的，但是有最优解为

得到

求得   

最小二乘法的原理就是空间的投影，不仅可以拟合曲线还可以用来求一些问题的最优解等，例如多项式插值等。