[论文阅读笔记16]BoT-SORT论文公式推导与代码解读
论文地址: BoT-SORT: Robust Associations Multi-Pedestrian Tracking
和OCSORT(解读见OCSORT)一样, 都是对Kalman滤波进行的改进. OCSORT是针对观测(检测器)不可靠时Kalman预测方差变大的问题, 对轨迹做了平滑. 而BoT-SORT是针对相机运动的问题, 加入了相机运动补偿. 也就是除了利用Kalman预测目标的新位置之外, 还利用稀疏光流(也就是提取目标之外的画面中的关键点, 来获得两帧之间画面的移动, 进而补偿Kalman得到的结果)
1. Kalman滤波
Kalman滤波遵循如下的更新步骤和预测步骤:
预测步:
x ^ t ∣ t − 1 = F t x ^ t − 1 ∣ t − 1 + B t u t P t ∣ t − 1 = F t P t − 1 ∣ t − 1 F t + Q \hat{x}_{t|t-1}=F_t\hat{x}_{t-1|t-1}+B_tu_t \\ P_{t|t-1}=F_tP_{t-1|t-1}F_t+Q x^t∣t−1=Ftx^t−1∣t−1+BtutPt∣t−1=FtPt−1∣t−1Ft+Q
更新步:
x ^ t ∣ t = x ^ t ∣ t − 1 + K t ( z t − H t x ^ t ∣ t − 1 ) K t = P t ∣ t − 1 H t T H t T P t ∣ t − 1 H t + R t P t ∣ t = P t ∣ t − 1 − K t H t P t ∣ t − 1 \hat{x}_{t|t}=\hat{x}_{t|t-1}+K_t(z_t-H_t\hat{x}_{t|t-1})\\ K_t=\frac{P_{t|t-1}H_t^T}{H_t^TP_{t|t-1}H_t+R_t}\\ P_{t|t}=P_{t|t-1}-K_tH_tP_{t|t-1} x^t∣t=x^t∣t−1+Kt(zt−Htx^t∣t−1)Kt=HtTPt∣t−1Ht+RtPt∣t−1HtTPt∣t=Pt∣t−1−KtHtPt∣t−1
其中 Q Q Q, R R R分别为输入(观测)和状态的噪声的协方差矩阵.
2. 状态变量的选择
在SORT中, 状态变量为[中心点, 面积, 高宽比, 速度, 面积变化率], 即 x = [ x c , y c , a , s , x c ˙ , y c ˙ , s ˙ ] x=[x_c, y_c, a ,s, \dot{x_c}, \dot{y_c}, \dot{s}] x=[xc,yc,a,s,xc˙,yc˙,s˙], 从DeepSORT以后, 状态变量基本采用的是 x = [ x c , y c , a , h , x c ˙ , y c ˙ , a ˙ , h ˙ ] x=[x_c, y_c, a, h, \dot{x_c}, \dot{y_c}, \dot{a}, \dot{h}] x=[xc,yc,a,h,xc˙,yc˙,a˙,h˙].
在BoT-SORT中, 作者简单地将状态变量改成了xywh及其导数, 即: x = [ x c , y c , w , h , x c ˙ , y c ˙ , w ˙ , h ˙ ] x=[x_c, y_c, w, h, \dot{x_c}, \dot{y_c}, \dot{w}, \dot{h}] x=[xc,yc,w,h,xc˙,yc˙,w˙,h˙], 类似地, 观测器的输入变量为 z = [ z x c , z y c , z w , z h ] z=[z_{xc}, z_{yc}, z_w, z_h] z=[zxc,zyc,zw,zh].
论文(1)(2)式
论文(3)(4)式, 关于噪声协方差矩阵的定义暂时没看懂, 看懂后补充
从消融实验的结果看, 按照这种方式更改状态变量MOTA, IDF1和HOTA指标大约有0.1 0.2左右的提升
3. 相机运动补偿
这是BoT-SORT提出的核心思想.
由于相机运动, 可能会造成匹配的不准确. 然而我们缺乏相机运动的先验信息(例如导航等), 因此, 相邻两帧之间的图像配准(image registration)可以近似相机运动在图像二维平面上的投影.
这里可以理解为, 相机运动等同于坐标系的变换, 因此目标的位置, 运动方向等我们需要重新投影到新坐标系中, 因此我们需要求解坐标系的变换矩阵. 如下图所示:
![[论文阅读笔记16]BoT-SORT论文公式推导与代码解读_第1张图片](http://img.e-com-net.com/image/info8/e59be2f6539d4182a577d9a6ffd77412.jpg)
因此, 利用 RANSAC算法得到平面坐标变化的仿射矩阵, 描述2维平面旋转变化矩阵为 M ∈ R 2 × 2 M\in\mathbb{R}^{2\times 2} M∈R2×2, 平移变化向量为 T ∈ R 2 T\in\mathbb{R}^{2} T∈R2, 定义仿射矩阵
A = [ M T ] ∈ R 2 × 3 A = [M \quad T]\in\mathbb{R}^{2\times 3} A=[MT]∈R2×3
论文(5)式
假定Kalman预测后的结果为 x ^ t ∣ t − 1 = [ x c , y c , w , h , x c ˙ , y c ˙ , w ˙ , h ˙ ] T \hat{x}_{t|t-1}=[x_c, y_c, w, h, \dot{x_c}, \dot{y_c}, \dot{w}, \dot{h}]^T x^t∣t−1=[xc,yc,w,h,xc˙,yc˙,w˙,h˙]T, 我们需要对中心点和高宽都应用仿射变换, 为了用一次矩阵乘法实现, 构造:
M k ∣ k − 1 ′ = d i a g { M , M , M , M } ∈ R 8 × 8 T k ∣ k − 1 ′ = [ T , 0 , 0 , 0 , 0 , 0 , 0 ] ∈ R 8 M'_{k|k-1}=diag\{M, M, M, M\}\in\mathbb{R}^{8\times 8}\\ T'_{k|k-1}=[T ,0, 0, 0, 0, 0, 0]\in\mathbb{R}^{8} Mk∣k−1′=diag{M,M,M,M}∈R8×8Tk∣k−1′=[T,0,0,0,0,0,0]∈R8
因此:
x ^ t ∣ t − 1 ′ = M k ∣ k − 1 ′ x ^ t ∣ t − 1 + T k ∣ k − 1 ′ \hat{x}_{t|t-1}'=M'_{k|k-1}\hat{x}_{t|t-1}+T'_{k|k-1} x^t∣t−1′=Mk∣k−1′x^t∣t−1+Tk∣k−1′
x ^ t ∣ t − 1 \hat{x}_{t|t-1} x^t∣t−1的协方差矩阵变为(随机变量应用线性变换, 方差为系数平方关系):
P t ∣ t − 1 ′ = M k ∣ k − 1 ′ P t ∣ t − 1 M k ∣ k − 1 ′ T P_{t|t-1}'=M'_{k|k-1}P_{t|t-1}M^{'T}_{k|k-1} Pt∣t−1′=Mk∣k−1′Pt∣t−1Mk∣k−1′T
论文(5)~(8)式
随后利用修正后的 x ^ t ∣ t − 1 ′ \hat{x}_{t|t-1}' x^t∣t−1′和 P t ∣ t − 1 ′ P_{t|t-1}' Pt∣t−1′再进行更新步.
论文(9)式
在实现中, 我们将画面中的目标扣去, 在其余的部分检测关键点, 来计算仿射矩阵:(tracker\gmc.py line120)
# find the keypoints
mask = np.zeros_like(frame)
# mask[int(0.05 * height): int(0.95 * height), int(0.05 * width): int(0.95 * width)] = 255
mask[int(0.02 * height): int(0.98 * height), int(0.02 * width): int(0.98 * width)] = 255
if detections is not None:
for det in detections:
tlbr = (det[:4] / self.downscale).astype(np.int_)
mask[tlbr[1]:tlbr[3], tlbr[0]:tlbr[2]] = 0
keypoints = self.detector.detect(frame, mask)
# compute the descriptors
keypoints, descriptors = self.extractor.compute(frame, keypoints)
随后将相邻两帧的关键点进行匹配
# Match descriptors.
knnMatches = self.matcher.knnMatch(self.prevDescriptors, descriptors, 2)
如果关键点的个数足够, 就计算仿射矩阵
# Find rigid matrix
if (np.size(prevPoints, 0) > 4) and (np.size(prevPoints, 0) == np.size(prevPoints, 0)):
H, inliesrs = cv2.estimateAffinePartial2D(prevPoints, currPoints, cv2.RANSAC)
以上部分依赖于cv2库. 得到仿射矩阵后, 修正Kalman的结果(tracker\bot_sort.py line68):
def multi_gmc(stracks, H=np.eye(2, 3)):
if len(stracks) > 0:
multi_mean = np.asarray([st.mean.copy() for st in stracks])
multi_covariance = np.asarray([st.covariance for st in stracks])
R = H[:2, :2]
R8x8 = np.kron(np.eye(4, dtype=float), R)
t = H[:2, 2]
for i, (mean, cov) in enumerate(zip(multi_mean, multi_covariance)):
mean = R8x8.dot(mean)
mean[:2] += t
cov = R8x8.dot(cov).dot(R8x8.transpose())
stracks[i].mean = mean
stracks[i].covariance = cov
4. 匹配策略
在匹配过程中, 利用指数滑动平均来平衡过去和当前的外观特征, 随后将运动特征和外观特征线性组合作为cost matrix, 如下两式所示:
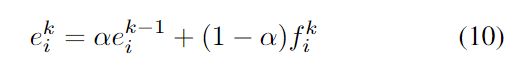
对于外观和IoU都相似的目标, 给予更小的cost, 否则设为1, 并以此更新C中的元素:
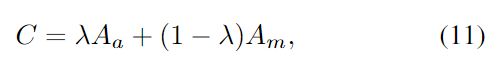
![[论文阅读笔记16]BoT-SORT论文公式推导与代码解读_第2张图片](http://img.e-com-net.com/image/info8/5e35222b9bea4b46b5b82c053d1c234a.jpg)
![[论文阅读笔记16]BoT-SORT论文公式推导与代码解读_第3张图片](http://img.e-com-net.com/image/info8/983a131bcfad44dfba8036fa2457dd04.jpg)