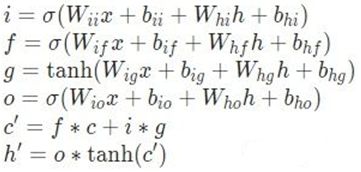一、需求背景
我们福禄网络致力于为广大用户提供智能化充值服务,包括各类通信充值卡(比如移动、联通、电信的话费及流量充值)、游戏类充值卡(比如王者荣耀、吃鸡类点券、AppleStore充值、Q币、斗鱼币等)、生活服务类(比如肯德基、小鹿茶等),网娱类(比如QQ各类钻等),作为一个服务提供商,商品质量的稳定、持续及充值过程的便捷一直是我们在业内的口碑。
在整个商品流通过程中,如何做好库存的管理,以充分提高库存运转周期和资金使用效率,一直是个难题。基于此,我们提出了智能化的库存管理服务,根据订单数据及商品数据,来预测不同商品随着时间推移的日常消耗情况。
二、算法选择
目前成熟的时间序列预测算法很多,但商业领域性能优越的却不多,经过多种尝试,给大家推荐2种时间序列算法:facebook开源的Prophet算法和LSTM深度学习算法。
现将个人理解的2种算法特性予以简要说明:
- (1)、在训练时间上,prophet几十秒就能出结果,而lstm往往需要1个半小时,更是随着网络层数和特征数量的增加而增加。
- (2)、Prophet是一个为商业预测而生的时间序列预测模型,因此在很多方便都有针对性的优化,而lstm的初衷是nlp。
- (3)、Prophet无需特征处理即可使用,参数调优也明确简单。而lstm则需要先进行必要的特征处理,其次要进行正确的网络结构设计,因此lstm相对prophet更为复杂。
- (4)、Lstm需要更多的数据进行学习,否则无法消除欠拟合的情形。而prophet不同,prophet基于统计学,有完整的数学理论支撑,因此更容易从少量的数据中完成学习。
- (5)、传统的时间序列预测算法只支持单纬度,但LSTM能支持多纬度,也就是说LSTM能考虑促销活动,目标用户特性,产品特性等
三、数据来源
- (1)、订单数据
- (2)、产品分类数据
四、数据形式
time,product,cnt
2019-10-01 00,**充值,6
2019-10-01 00,***游戏,368
2019-10-01 00,***,1
2019-10-01 00,***,11
2019-10-01 00,***游戏,17
2019-10-01 00
,三网***,39
2019-10-01 00,**网,6
2019-10-01 00,***,2字段说明:
- Time:小时级时间
- Product:产品名称或产品的分类名称,目前使用的是产品2级分类,名称
- Cnt:成功订单数量
目前的时间序列是由以上time和cnt组成,product是用于区分不同时间序列的字段。
五、特征处理
时间序列一般不进行特征处理,当然可以根据具体情况进行归一化处理或是取对数处理等。
六、算法选择
目前待选的算法主要有2种:
- (1)、Prophet
Facebook开源的时间序列预测算法,考虑了节假日因素。 - (2)、LSTM
优化后的RNN深度学习算法。
七、算法说明
7.1 prophet
7.1.1Prophet的核心是调参,步骤如下:
- 1、首先我们去除数据中的异常点(outlier),直接赋值为none就可以,因为Prophet的设计中可以通过插值处理缺失值,但是对异常值比较敏感。
- 2、选择趋势模型,默认使用分段线性的趋势,但是如果认为模型的趋势是按照log函数方式增长的,可设置growth='logistic'从而使用分段log的增长方式
- 3、 设置趋势转折点(changepoint),如果我们知道时间序列的趋势会在某些位置发现转变,可以进行人工设置,比如某一天有新产品上线会影响我们的走势,我们可以将这个时刻设置为转折点。如果自己不设置,算法会自己总结changepoint。
- 4、 设置周期性,模型默认是带有年和星期以及天的周期性,其他月、小时的周期性需要自己根据数据的特征进行设置,或者设置将年和星期等周期关闭。
设置节假日特征,如果我们的数据存在节假日的突增或者突降,我们可以设置holiday参数来进行调节,可以设置不同的holiday,例如五一一种,国庆一种,影响大小不一样,时间段也不一样。 - 5、 此时可以简单的进行作图观察,然后可以根据经验继续调节上述模型参数,同时根据模型是否过拟合以及对什么成分过拟合,我们可以对应调节seasonality_prior_scale、holidays_prior_scale、changepoint_prior_scale参数。
以上是理论上的调参步骤,但我们在实际情况下在建议使用grid_search(网格寻参)方式,直接简单效果好。当机器性能不佳时网格调参配合理论调参方法可以加快调参速度。建议初学者使用手动调参方式以理解每个参数对模型效果的影响。
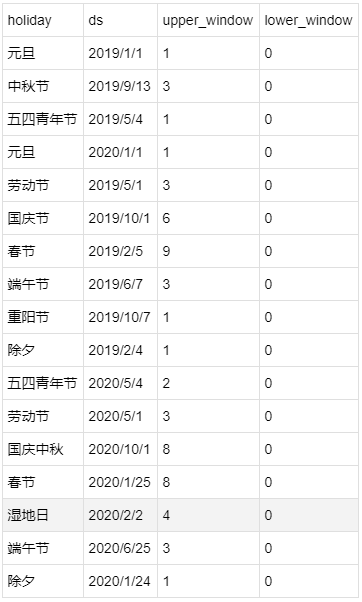
holiday.csv
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from fbprophet import Prophet
data = pd.read_csv('../data/data2.csv', parse_dates=['time'], index_col='time')
def get_product_data(name, rule=None):
product = data[data['product'] == name][['cnt']]
product.plot()
if rule is not None:
product = product.resample(rule).sum()
product.reset_index(inplace=True)
product.columns = ['ds', 'y']
return product
holidays = pd.read_csv('holiday.csv', parse_dates=['ds'])
holidays['lower_window'] = -1
holidays = holidays.append(pd.DataFrame({
'holiday': '双11',
'ds': pd.to_datetime(['2019-11-11', '2020-11-11']),
'lower_window': -1,
'upper_window': 1,
})).append(pd.DataFrame({
'holiday': '双12',
'ds': pd.to_datetime(['2019-12-12', '2020-12-12']),
'lower_window': -1,
'upper_window': 1,
})
)
def predict(name, rule='1d', freq='d', periods=1, show=False):
ds = get_product_data(name, rule=rule)
if ds.shape[0] < 7:
return None
m = Prophet(holidays=holidays)
m.fit(ds)
future = m.make_future_dataframe(freq=freq, periods=periods) # 建立数据预测框架,数据粒度为天,预测步长为一年
forecast = m.predict(future)
if show:
m.plot(forecast).show() # 绘制预测效果图
m.plot_components(forecast).show() # 绘制成分趋势图
mse = forecast['yhat'].iloc[ds.shape[0]] - ds['y'].values
mse = np.abs(mse) / (ds['y'].values + 1)
return [name, mse.mean(), mse.max(), mse.min(), np.quantile(mse, 0.9), np.quantile(mse, 0.8), mse[-7:].mean(),
ds['y'].iloc[-7:].mean()]
if __name__ == '__main__':
products = set(data['product'])
p = []
for i in products:
y = predict(i)
if y is not None:
p.append(y)
df = pd.DataFrame(p, columns=['product', 'total_mean', 'total_max', 'total_min', '0.9', '0.8', '7_mean',
'7_real_value_mean'])
df.set_index('product', inplace=True)
product_sum: pd.DataFrame = data.groupby('product').sum()
df = df.join(product_sum)
df.sort_values('cnt', ascending=False, inplace=True)
df.to_csv('result.csv', index=False)结果如下:由于行数较多这里只展示前1行
根据结果,对比原生数据,可以得出如下结论:
就算法与产品的匹配性可分为3个类型:
- (1)与算法较为匹配,算法的历史误差8分为数<=0.2的
- (2)与算法不太匹配的,算法的历史误差8分为数>0.2的
- (3)数据过少的,无法正常预测的。目前仅top10就能占到整体订单数的90%以上。
7.1.2 部分成果展示
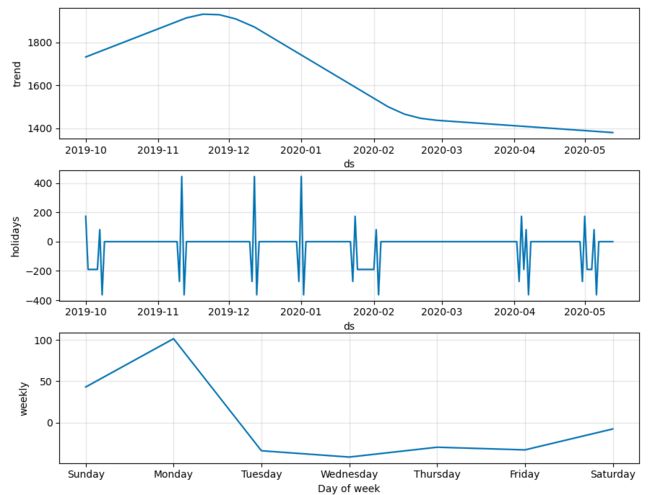
A. 因素分解图
上图中主要分为3个部分,分别对应prophet 3大要素,趋势、节假日或特殊日期、周期性(包括年周期、月周期、week周期、天周期以及用户自定义的周期)
下面依照上面因素分解图的顺序依次对图进行说明:
- (1)、Trend:
即趋势因素图。描述时间序列的趋势。Prophet支持线性趋势和logist趋势。通过growth参数设置,当然模型能自己根据时间序列的走势判断growth类型。这也是prophet实现的比较智能的一点。 - (2)、Holidays
即节假日及特殊日期因素图。描述了节假日及用户自定义的特殊日期对时间序列的影响。正值为正影响,负值为负影响。从图中可以看出这个商品对节假日比较敏感。节假日是根据holidays参数设置的。 - (3)、weekly
星期周期性因素图。正常情况下,如果是小时级别数据将会有天周期图。有1年以上完整数据并且时间序列有典型的年周期性会有年周期图。如果你觉得这个有年周期,但模型并不这么认为,你可以通过设置yearly_seasonality设置一个具体的数值。这个数值默认情况下为10(weekly_seasonality默认为3),这个值代表的是傅里叶级数的项数,越大模型越容易过拟合,过小则会导致欠拟合,一般配合seasonality_prior_scale使用。
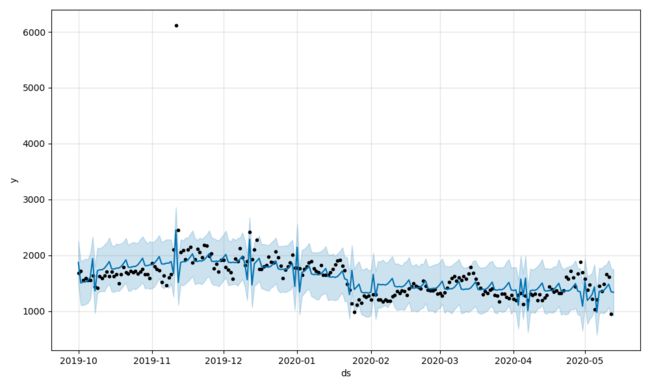
B.预测曲线与实际值对比
7.2 lstm
LSTM(长短记忆网络)主要用于有先后顺序的序列类型的数据的深度学习网络。是RNN的优化版本。一般用于自然语言处理,也可用于时间序列的预测。
简单来说就是,LSTM一共有三个门,输入门,遗忘门,输出门, i 、o、 f 分别为三个门的程度参数, g 与RNN中的概念一致。公式里可以看到LSTM的输出有两个,细胞状态c 和隐状态 h,c是经输入、遗忘门的产物,也就是当前cell本身的内容,经过输出门得到h,就是想输出什么内容给下一单元。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import torch
from torch import nn
from sklearn.preprocessing import MinMaxScaler
ts_data = pd.read_csv('../data/data2.csv', parse_dates=['time'], index_col='time')
def series_to_supervised(data, n_in=1, n_out=1, dropnan=True):
n_vars = 1 if type(data) is list else data.shape[1]
df = pd.DataFrame(data)
cols, names = list(), list()
# input sequence (t-n, ... t-1)
for i in range(n_in, 0, -1):
cols.append(df.shift(i))
names += [('var%d(t-%d)' % (j + 1, i)) for j in range(n_vars)]
# forecast sequence (t, t+1, ... t+n)
for i in range(0, n_out):
cols.append(df.shift(-i))
if i == 0:
names += [('var%d(t)' % (j + 1)) for j in range(n_vars)]
else:
names += [('var%d(t+%d)' % (j + 1, i)) for j in range(n_vars)]
# put it all together
agg = pd.concat(cols, axis=1)
agg.columns = names
# drop rows with NaN values
if dropnan:
agg.dropna(inplace=True)
return agg
def transform_data(feature_cnt=2):
yd = ts_data[ts_data['product'] == '移动话费'][['cnt']]
scaler = MinMaxScaler(feature_range=(0, 1))
yd_scaled = scaler.fit_transform(yd.values)
yd_renamed = series_to_supervised(yd_scaled
, n_in=feature_cnt).values.astype('float32')
n_row = yd_renamed.shape[0]
n_train = int(n_row * 0.7)
train_X, train_y = yd_renamed[:n_train, :-1], yd_renamed[:n_train, -1]
test_X, test_y = yd_renamed[n_train:, :-1], yd_renamed[n_train:, -1]
# 最后,我们需要将数据改变一下形状,因为 RNN 读入的数据维度是 (seq, batch, feature),所以要重新改变一下数据的维度,这里只有一个序列,所以 batch 是 1,而输入的 feature 就是我们希望依据的几天,这里我们定的是两个天,所以 feature 就是 2.
train_X = train_X.reshape((-1, 1, feature_cnt))
test_X = test_X.reshape((-1, 1, feature_cnt))
print(train_X.shape, train_y.shape, test_X.shape, test_y.shape)
# 转化成torch 的张量
train_x = torch.from_numpy(train_X)
train_y = torch.from_numpy(train_y)
test_x = torch.from_numpy(test_X)
test_y = torch.from_numpy(test_y)
return scaler, train_x, train_y, test_x, test_y
scaler, train_x, train_y, test_x, test_y = transform_data(24)
# lstm 网络
class lstm_reg(nn.Module): # 括号中的是python的类继承语法,父类是nn.Module类 不是参数的意思
def __init__(self, input_size, hidden_size, output_size=1, num_layers=2): # 构造函数
# inpu_size 是输入的样本的特征维度, hidden_size 是LSTM层的神经元个数,
# output_size是输出的特征维度
super(lstm_reg, self).__init__() # super用于多层继承使用,必须要有的操作
self.rnn = nn.LSTM(input_size, hidden_size, num_layers) # 两层LSTM网络,
self.reg = nn.Linear(hidden_size, output_size) # 把上一层总共hidden_size个的神经元的输出向量作为输入向量,然后回归到output_size维度的输出向量中
def forward(self, x): # x是输入的数据
x, _ = self.rnn(x) # 单个下划线表示不在意的变量,这里是LSTM网络输出的两个隐藏层状态
s, b, h = x.shape
x = x.view(s * b, h)
x = self.reg(x)
x = x.view(s, b, -1) # 使用-1表示第三个维度自动根据原来的shape 和已经定了的s,b来确定
return x
def train(feature_cnt, hidden_size, round, save_path='model.pkl'):
# 我使用了GPU加速,如果不用的话需要把.cuda()给注释掉
net = lstm_reg(feature_cnt, hidden_size)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(net.parameters(), lr=1e-2)
for e in range(round):
# 新版本中可以不使用Variable了
# var_x = Variable(train_x).cuda()
# var_y = Variable(train_y).cuda()
# 将tensor放在GPU上面进行运算
var_x = train_x
var_y = train_y
out = net(var_x)
loss = criterion(out, var_y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if (e + 1) % 100 == 0:
print('Epoch: {}, Loss:{:.5f}'.format(e + 1, loss.item()))
# 存储训练好的模型参数
torch.save(net.state_dict(), save_path)
return net
if __name__ == '__main__':
net = train(24, 8, 5000)
# criterion = nn.MSELoss()
# optimizer = torch.optim.Adam(net.parameters(), lr=1e-2)
pred_test = net(test_x) # 测试集的预测结果
pred_test = pred_test.view(-1).data.numpy() # 先转移到cpu上才能转换为numpy
# 乘以原来归一化的刻度放缩回到原来的值域
origin_test_Y = scaler.inverse_transform(test_y.reshape((-1,1)))
origin_pred_test = scaler.inverse_transform(pred_test.reshape((-1,1)))
# 画图
plt.plot(origin_pred_test, 'r', label='prediction')
plt.plot(origin_test_Y, 'b', label='real')
plt.legend(loc='best')
plt.show()
# 计算MSE
# loss = criterion(out, var_y)?
true_data = origin_test_Y
true_data = np.array(true_data)
true_data = np.squeeze(true_data) # 从二维变成一维
MSE = true_data - origin_pred_test
MSE = MSE * MSE
MSE_loss = sum(MSE) / len(MSE)
print(MSE_loss)八、两种算法的比较
- (1)在训练时间上,prophet几十秒就能出结果,而lstm往往需要1个半小时,更是随着网络层数和特征数量的增加而增加。
- (2)Prophet是一个为商业预测而生的时间序列预测模型,因此在很多方便都有针对性的优化,而lstm的初衷是nlp。
- (3)Prophet无需特征处理即可使用,参数调优也明确简单。而lstm则需要先进行必要的特征处理,其次要进行正确的网络结构设计,因此lstm相对prophet更为复杂。
- (4)Lstm需要更多的数据进行学习,否则无法消除欠拟合的情形。而prophet不同,prophet基于统计学,有完整的数学理论支撑,因此更容易从少量的数据中完成学习。
参考文献:
【1】Prophet官方文档:https://facebook.github.io/prophet/
【2】Prophet论文:https://peerj.com/preprints/3190/
【3】Prophet-github:https://github.com/facebook/prophet
【4】LSTM http://colah.github.io/posts/2015-08-Understanding-LSTMs/
【5】基于LSTM的关联时间序列预测方法研究 尹康 《北京交通大学》 2019年 cnki地址:http://cdmd.cnki.com.cn/Article/CDMD-10004-1019209125.htm