9. 卷积神经网络的简单理解及实现
一、理论知识
对于全连接神经网络，如果第 
层有 
个神经元，第 
层有 
个神经元，那么权重矩阵有 
个参数。当 和 都很大时，权重矩阵的参数非常多，训练效率会非常低。
1. 卷积层
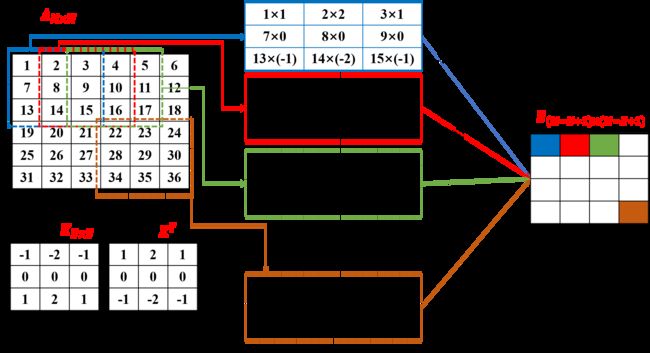
卷积层的作用是提取一个局部区域的特征，不同的卷积核相当于不同的特征提取器。
假设输入数据为M×M二维矩阵，经过N×N的卷积核变换后，得到(M-N+1)×(M-N+1)的特征矩阵。
下图表示的是对二维矩阵样本数据进行卷积操作的演示
2. 池化层
池化层的作用是进行特征选择，降低特征数量，从而减少参数数量。
常用的池化函数有两种：
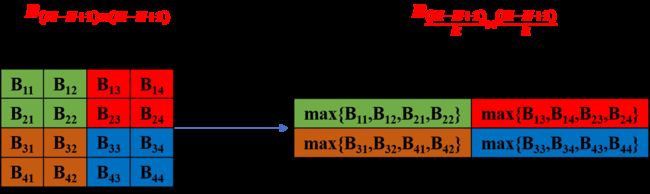
2.1 最大池化
选择这个区域内所有神经元的最大活性值作为这个区域的表示，如下图所示。
2.2 平均池化
提取区域内所有神经元活性值的平均值。
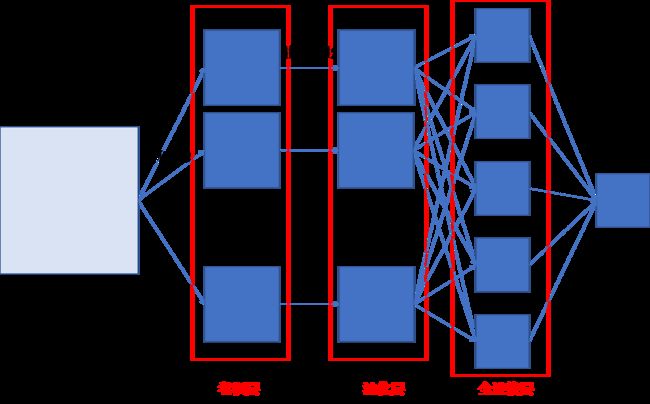
3. 卷积神经网络的完整结构
一个典型的卷积网络是由卷积层、池化层、全连接层组成。一般卷积核个数设置在2~5，池化层的0~1。卷积核加池化层为一个卷积网块，一般比较多（1~100或者更大）。全连接的层数一般设置在0~2。
重点：整个网络数据传递的Size
以MNIST数据为例，输入数据的Size
[64, 1, 28, 28] #每次传递64张图片，每个图片只有一个通道，每个通道下的像素点为28乘28；
基于卷积操作，每个图片提取5个特征，卷积核其大小为[4,4]，则卷积层数据的Size为
[64, 5, 25, 25] # [64, 5, 28-4+1, 28-4+1] 64个图片，每张图片5个通道，每个通道下特征像素为25乘25；
基于池化操作，最大池化矩阵的大小为[5,5]，则池化层数据的Size为
[64, 5, 5, 5] # [64,5,25/5,25/5] # [64, 5, 28-4+1, 28-4+1] 64个图片，每张图片5个通道，每个通道下最大像素特征矩阵降低至5乘5；
全连接层操作，数据的Size为
[64, 125] # [64, 5*5*5]
二、基于PyTorch搭建简单的卷积神经网络架构
class ConvNet(nn.Module):
def __init__(self):
super(ConvNet, self).__init__()
# 卷积层
self.layer1 = nn.Conv2d(1, 5, kernel_size=4)
self.layer2 = nn.ReLU()
# 池化层
self.layer3 = nn.MaxPool2d(kernel_size=5)
# 全连接层
self.layer4 = nn.Linear(5*5*5, 50)
self.layer5 = nn.ReLU()
self.layer6 = nn.Linear(50, 10)
def forward(self,x):
# [64, 1, 28, 28] -> [64, 5, 25, 25]
x = self.layer1(x)
x = self.layer2(x)
# [64, 5, 25, 25] -> [64, 5, 5, 5]
x = self.layer3(x)
# [64, 5, 5, 5] -> [64,5*5*5]
x = x.view(data.size(0),5*5*5)
# [64,5*5*5] -> [64,50]
x = self.layer4(x)
x = self.layer5(x)
# [64,50] -> [64,10]
out = self.layer6(x)
return out三、基于卷积神经网络架构对MNIST数据集的训练
除神经网络框架构建外，其余操作与前文一致
from torchvision.datasets import MNIST
from torchvision.transforms import ToTensor
from torch.utils.data import DataLoader
import torch
import torch.nn as nn
from torch.optim.sgd import SGD
import matplotlib.pyplot as plt
batch_size = 64
class ConvNet(nn.Module):
def __init__(self):
super(ConvNet, self).__init__()
# 卷积层
self.layer1 = nn.Conv2d(1, 5, kernel_size=4)
self.layer2 = nn.ReLU()
# 池化层
self.layer3 = nn.MaxPool2d(kernel_size=5)
# 全连接层
self.layer4 = nn.Linear(5*5*5, 50)
self.layer5 = nn.ReLU()
self.layer6 = nn.Linear(50, 10)
def forward(self,x):
# [64, 1, 28, 28] -> [64, 5, 25, 25]
x = self.layer1(x)
x = self.layer2(x)
# [64, 5, 25, 25] -> [64, 5, 5, 5]
x = self.layer3(x)
# [64, 5, 5, 5] -> [64,5*5*5]
x = x.view(data.size(0),5*5*5)
# [64,5*5*5] -> [64,50]
x = self.layer4(x)
x = self.layer5(x)
# [64,50] -> [64,10]
out = self.layer6(x)
return out
############################Step 2: 数据集下载##################################
trainData = MNIST(root = "./",
train = True,
transform=ToTensor(),
download = True)
testData = MNIST(root = "./",
train = False,
transform=ToTensor(),
download = True)
############################Step 3: 数据集加载##################################
trainData_loader = DataLoader(dataset = trainData,
batch_size = batch_size,
shuffle = True)
testData_loader = DataLoader(dataset = testData,
batch_size = batch_size,
shuffle = True)
#######################Step 4: 标签编码#########################################
def one_hot(label,depth=10):
out = torch.zeros(label.size(0),depth)
idx = torch.LongTensor(label).view(-1,1)
out.scatter_(dim=1,index=idx,value=1)
return out
###############################################################################
CN_model = ConvNet() # 定义网络具体参数
L = nn.CrossEntropyLoss() # 交叉熵损失函数
optimizer = SGD(CN_model.parameters(),lr=0.1) # 最小梯度优化算法
progress = []
loss_degree = []
####################### Step 5: 机器学习 ################################
for idx,(data,label) in enumerate(trainData_loader):
optimizer.zero_grad() #梯度清零
y_pred = CN_model(data) #正向学习
y = one_hot(label)
loss = L(y_pred,y) #计算误差
loss.backward() #反向传播，计算参数
optimizer.step() #参数更新
progress.append(100. * idx / len(trainData_loader))
loss_degree.append(loss.item())
plt.figure(dpi=300)
plt.plot(progress,loss_degree)
plt.xlabel("Progess (%)")
plt.ylabel("CrossEntropy Loss")
plt.xlim([0,100])
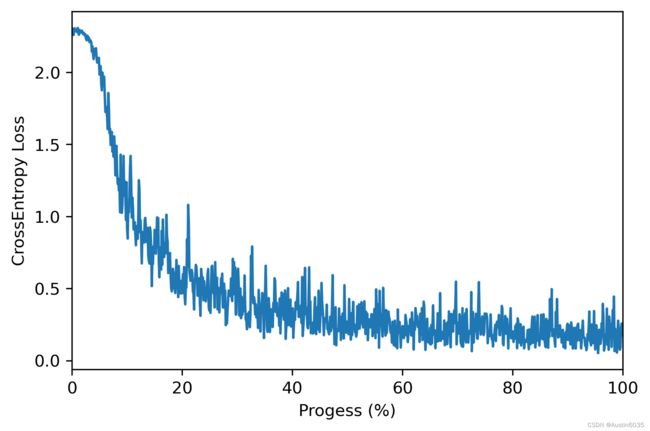
plt.show()训练结果的可视化
